在1.2节介绍图解法时，已直观地看到可行域和最优解的几何意义，在此从理论上进一步讨论。

（1）凸集 设K是n维空间的一个点集，对任意两点X（1）、X（2）∈K，当X=aX（1）+（1-α）X（2）∈K（0≤α≤1）时，则称K为凸集。

从直观上讲，凸集没有凹入部分，其内部没有空洞。实心圆、实心球体、实心立方体等都是凸集，圆环不是凸集。图1-7a所示是凸集，图1-7b所示不是凸集。任何两个凸集的交集是凸集，如图1-7c所示。

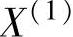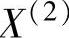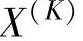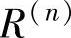（2）凸组合 设X，，，…，是中的一点，若存在λ₁，λ₂，…，λ_n，且λ_i≥0及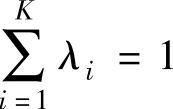，使得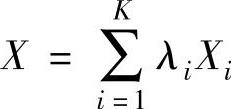成立，则称X为X（1），X（2），…，X（K）的凸组合。

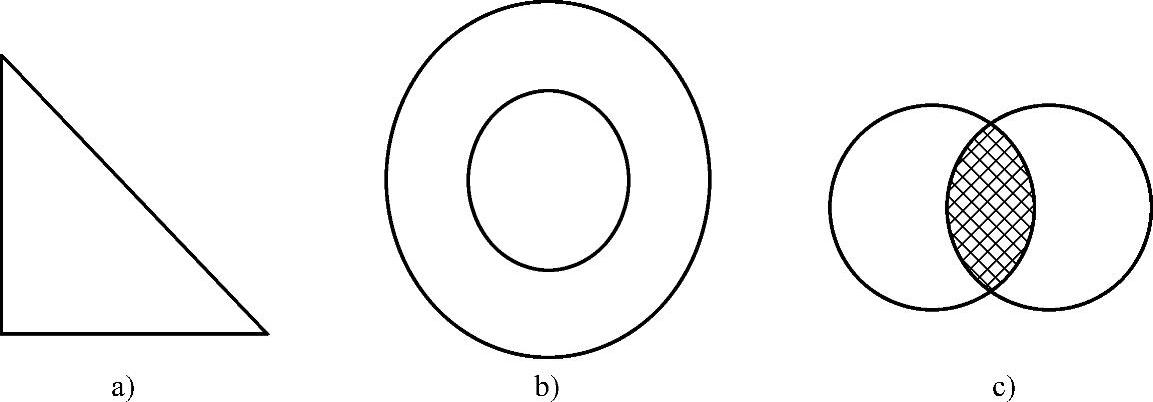
图1-7

（3）极点 设K是凸集，X∈K，若X不能用K中两个不同的点X^（1），X^（2）的凸组合表

示为：

X=αX^（1）+（1_-α）X^（2） （0＜α＜1）

则称X是K的一个极点（或顶点）。X是凸集K的极点，即X不可能是K中某一线段的内点，只能是K中某一线段的端点。(www.daowen.com)

（4）几个定理

【定理1.1】 若线性规划的可行解K非空，则K是凸集。

【定理1.2】 若线性规划的可行解集合K的点X是极点，其充要条件为X是基本可行解。

【定理1.3】 若线性规划有最优解，则最优解一定可以在可行解集合的某个极点上得到。

定理1.1描述了可行解集的几何特征。

定理1.2描述了可行解集的极点与基本可行解的对应关系。极点是基本可行解，基本可行解在极点上，但它们并非一一对应，可能有两个或几个基本可行解对应于同一个极点（退化基本可行解）。

定理1.3描述了最优解在可行解集中的位置。若最优解唯一，则最优解只能在某一极点上达到；若具有多重最优解，则最优解是在某些极点上的凸组合。因此，最优解是可行解集的极点或界点，不可能是可行解集的内点。

由定理1.2和定理1.3可知，线性规划的最优解是在有限个基本可行解中求得的，这样我们可以找到一种解题方法：先求出可行域的所有顶点，然后计算这些顶点的目标函数值，取最大的值为最优值，其相应的顶点坐标就是最优解。但当m、n较大时，这种方法是不可行的。

综上所述，若线性规划的可行解集非空且有界，则一定有最优解；若可行解集无界，则线性规划可能有最优解，也可能没有最优解。若线性规划具有无界解，则可行域一定无界。