已知线性规划的标准型为：

maxZ=CX

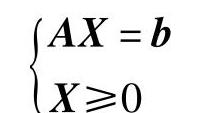
（1）基式中A是m×n矩阵，m≤n且r（A）=m，显然A中至少有一个m×m阶子矩阵B，使得r（B）=m。B是矩阵A中m×m阶非奇异子矩阵，则称B是线性规划的一个基（或基矩阵）。当m=n时，基矩阵唯一，当m<n时，基矩阵就可能有多个，但最多不超过。

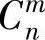【例1.7】 已知线性规划

maxZ=4x₁-2x₂-x₃

求其所有基矩阵。

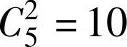解 约束方程的系数矩阵为2×5矩阵，r（A）=2，则其子矩阵为个，其中第1列和第3列构成的2阶矩阵不是一个基，基矩阵为以下9个：

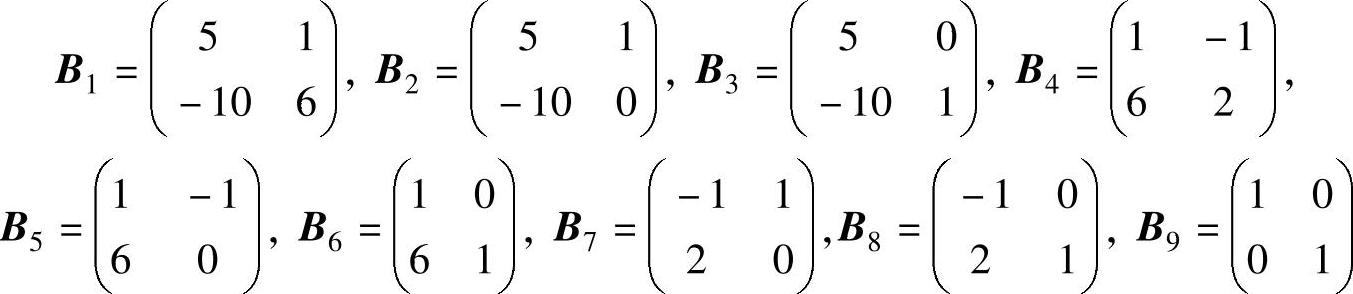
（2）基向量、非基向量、基变量、非基变量 当确定某一子矩阵为基矩阵时，则基矩阵对应的列向量称为基向量，其余列向量称为非基向量，基向量对应的变量称为基变量，非基向量对应的变量称为非基变量。

基变量和非基变量是针对某一确定基而言的，不同的基对应的基变量和非基变量不同。例1.7中B₁的基向量是A中的第1列和第2列，其余列向量是非基向量，x₁、x₂是基变量，x₃、x₄、x₅是非基变量；B₂的基向量是A中的第1列和第4列，其余列向量是非基向量，x₁、x₄是基变量，x₂、x₃、x₅是非基变量。(www.daowen.com)

（3）基本解 对某一确定基B，令非基变量等于零，利用约束条件AX=b解出基变量，则这组解称为基B的基本解。例1.7中对于B₉而言，X=（0，0，0，3，2）是其基本解。

（4）可行解 满足约束条件的解X=（x₁，x₂，…，x_n）T称为可行解。

（5）最优解 满足目标函数的可行解称为最优解，即使得目标函数达到极值的可行解就是最优解。

（6）基本可行解 满足非负条件的基本解称为基本可行解（也称基可行解）。在例1.7中，X=（0，0，0，3，2）既是基本解，又满足条件x_j≥0，则其是一个基本可行解。

（7）基本最优解 最优解是基本解称为基本最优解。例1.7中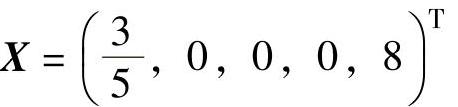是最优解，同时又是B₃的基本解，因此它是基本最优解。

当最优解唯一时，最优解也是基本最优解。当最优解不唯一时，则最优解不一定是基本最优解。

（8）可行基与最优基 基可行解对应的基称为可行基，基本最优解对应的基称为最优基。最优基也是可行基。

基本解、可行解、最优解、基本可行解、基本最优解的关系如图1-6所示。箭尾的解一定是箭头的解，否则不一定成立。

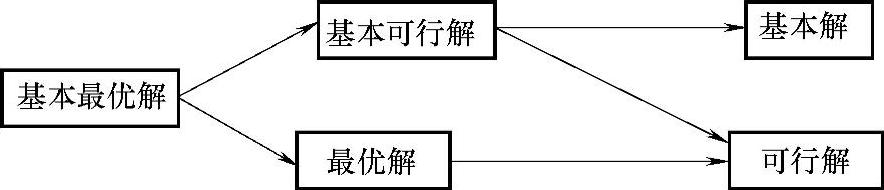
图1-6