线性规划问题有各种不同的形式。对目标函数，有的要求实现最大化，有的要求最小化；约束条件可以是“≥”形式的不等式，也可以是“≤”形式的不等式，也可以是等式；决策变量通常是非负约束，但也允许在（-∞，∞）范围内取值，即无约束。在用单纯形法求解线性规划问题时，为了讨论问题方便，需将线性规划模型变换为统一的标准形式。线性规划问题的标准型为：

1）目标函数求最大值（也可以求最小值）。

2）约束条件均为等式方程。

3）变量x_j为非负。

4）常数b_i都大于或等于零。

数学模型可表示为：

max（min）Z=c₁x₁+c₂x₂+…+c_nx_n

或写成下列形式：

用向量和矩阵表示该线性规划问题，可以使数学模型更简洁，即：

maxZ=CX

式中

A——约束方程的m×n维系数矩阵，一般m≤n，且A的秩为m，记为r（A）=m；

b——资源向量；

C——价值向量；

X——决策变量向量。(www.daowen.com)

实际问题提出的线性规划问题的数学模型都应变换为标准型后求解。以下讨论如何变换为标准型的问题。

1）若要求目标函数实现最小化，即minZ=CX。这时只需将目标函数最小化变换为目标函数最大化，即令Z′=-Z，于是得到maxZ′=-CX。

2）若约束方程为不等式。这里有两种情况：一种是约束方程为“≤”不等式，则可在不等式的左端加入非负松弛变量，把原不等式变为等式；另一种是约束方程为“≥”不等式，则可在不等式的左端减去一个非负剩余变量（也称松弛变量），把原不等式变为等式。

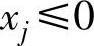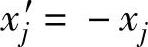3）若变量不满足x_j≥0。这里也有两种情况：一种是，可令，用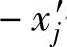代替x_j；另一种是x_j无约束，可令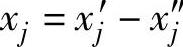，用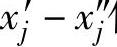代替x_j，其中，。

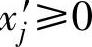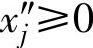4）若b_i≤0。这时只需将约束方程两边同时乘以-1。

下面举例说明。

【例1.6】 将下述线性规划问题变换为标准型。

minZ=-x₁+2x₂-3x₃

解

1）用x₄-x₅替换x₃，其中x₄，x₅≥0。

2）在第一个约束不等式“≤”号的左端加入松弛变量x₆。

3）在第二个约束不等式“≥”号的左端减去剩余变量x₇。

4）令Z′=-Z，把求minZ改为求maxZ′。得到该问题的标准型为：maxZ′=x₁-2x₂+3（x₄-x₅）+0x₆+0x₇