图解法是直接在平面直角坐标系中作图来解线性规划问题的一种方法。这种方法简单直观，有助于了解线性规划问题求解的基本原理，但它不是解线性规划问题的主要方法，只适合于求解两个变量的线性规划问题。

图解法的步骤：

1）可行域的确定。分别求出满足每个约束包括变量非负要求的区域，其交集就是可行解集合，称为可行域。

2）绘制目标函数等值线。先过原点作一条向量指向点（c₁，c₂），向量的方向就是目标函数增加的方向，称为梯度方向，再作一条与矢量垂直的直线，这条直线就是目标函数等值线。

3）求最优解。依据目标函数求最大或最小值来移动目标函数等值线，该直线与可行域边界相交的点对应的坐标就是最优解。一般情况下，求最大值时该直线沿着向量方向移动，求最小值时该直线沿着向量的反方向移动。

【例1.3】 用图解法求解下列线性规划问题：

maxZ=x₁+x₂

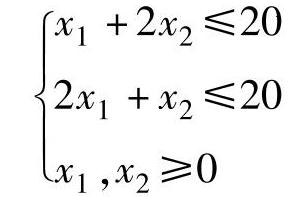
解：1）确定可行域。令三个约束条件为等式，得到三条直线，在第一象限画出满足三个不等式的区域，其交集就是可行域。

2）绘制目标函数等值线。将目标函数的系数组成一个坐标点（1，1），过原点O作一条向量指向点（1，1），矢量长度不限，矢量的斜率保持1，再作一条与向量垂直的直线，这条直线就是目标函数等值线，该直线的位置任意，如果其通过原点，则目标函数值Z=0，如图1-2所示。

3）求最优解。图1-2的向量方向是目标函数增加的方向或称为梯度方向，在求最大值时目标函数等值线沿着梯度方向平行移动（求最小值时将目标函数等值线沿着梯度方向的反方向平行移动），直到可行域的边界，停止移动，其交点对应的坐标就是最优解。如图1-2所示，最优解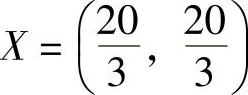，目标函数的最大值。

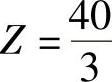上例中求解得到问题的最优解是唯一的，但对于一般线性规划问题，求解结果还可能出现以下几种情况：

（1）多重最优解（无穷多最优解）

【例1.4】 将例1.3的目标函数改为maxZ=4x₁+2x₂，约束条件不变，则表示目标函数中以参数Z的这组平行直线与约束条件2x₁+x₂≤20的边界线平行。平行移动目标函数直线与可行域相交于线段AB，则线段AB上任意点都是最优解，如图1-3所示，即最优解不唯一，有无穷多个，称为多重解。最优解的通解可表示为X=αX^（1）+（1-α）X^（2），0≤α≤1。(www.daowen.com)

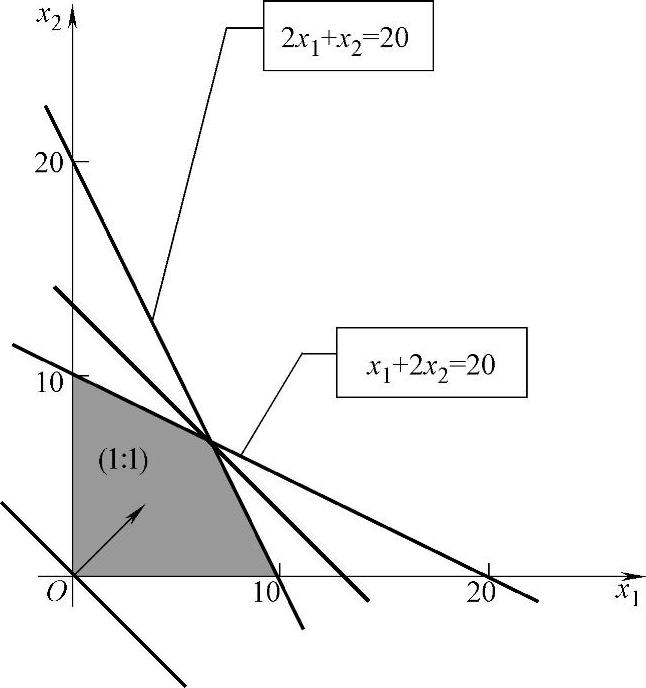
图1-2

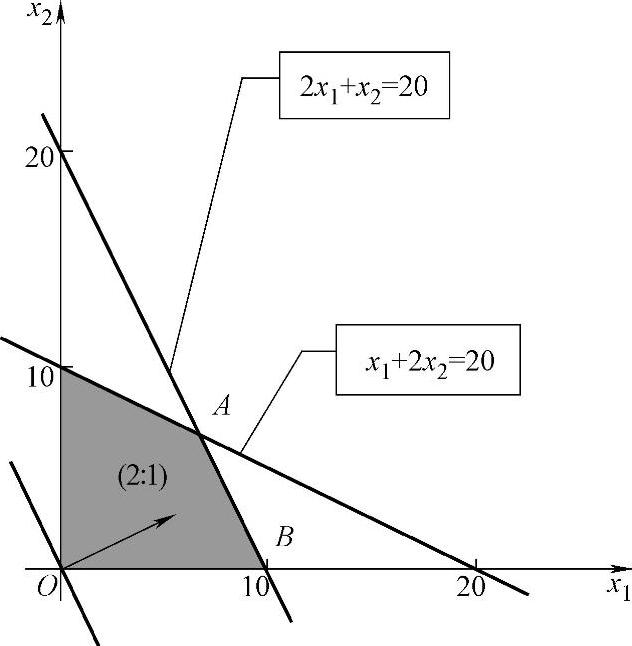
图1-3

（2）无界解【例1.5】 将例1.3的约束条件改为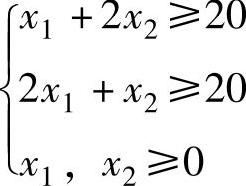，目标函数不变，则可行域如图1-4所示，目标函数增加的方向与例1.3相同，A点是最小值点，要达到最大值，目标函数值可在可行域中沿梯度方向继续平移直到无穷远，x₁、x₂及Z都趋于无穷大（无上界），这种情形称为无界解，即为无最优解。

（3）无可行解 在例1.3的数学模型中增加一个约束条件x₁+x₂≥30，则该问题的可行域为空集，如图1-5所示，即无可行解，因此该问题也就不存在最优解。

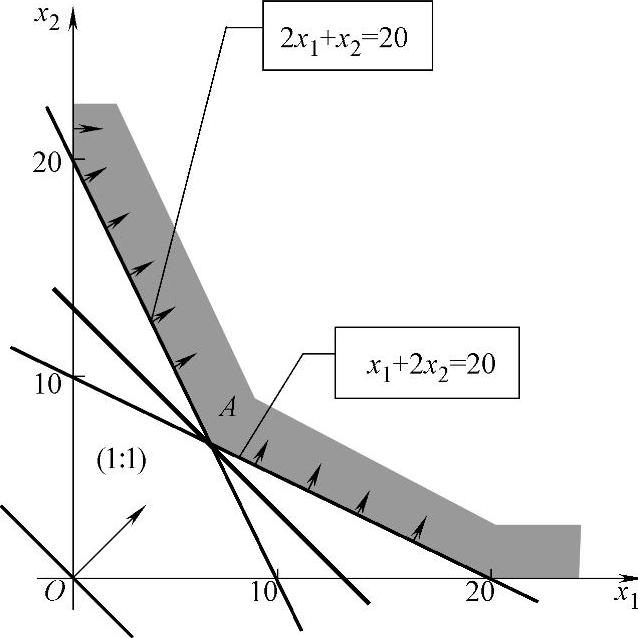
图1-4

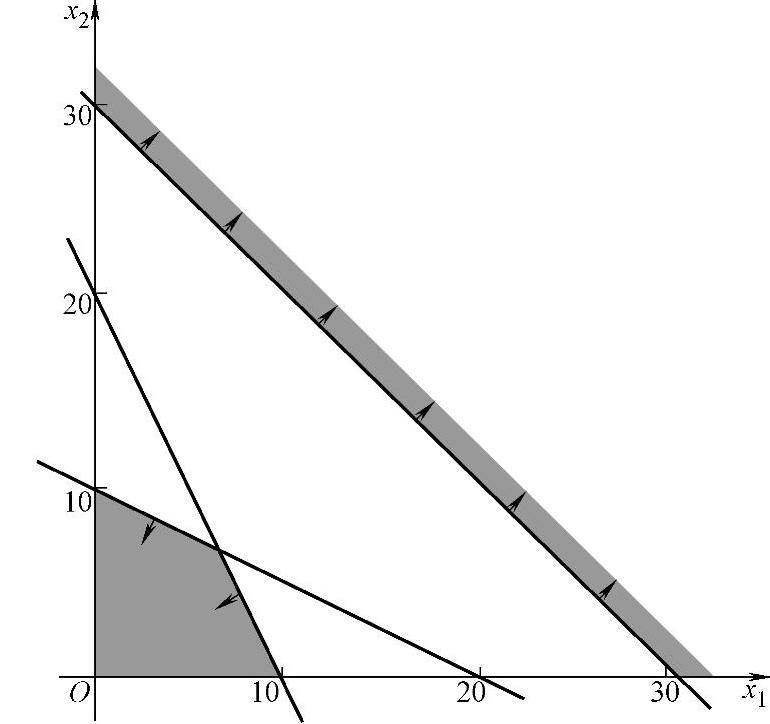
图1-5

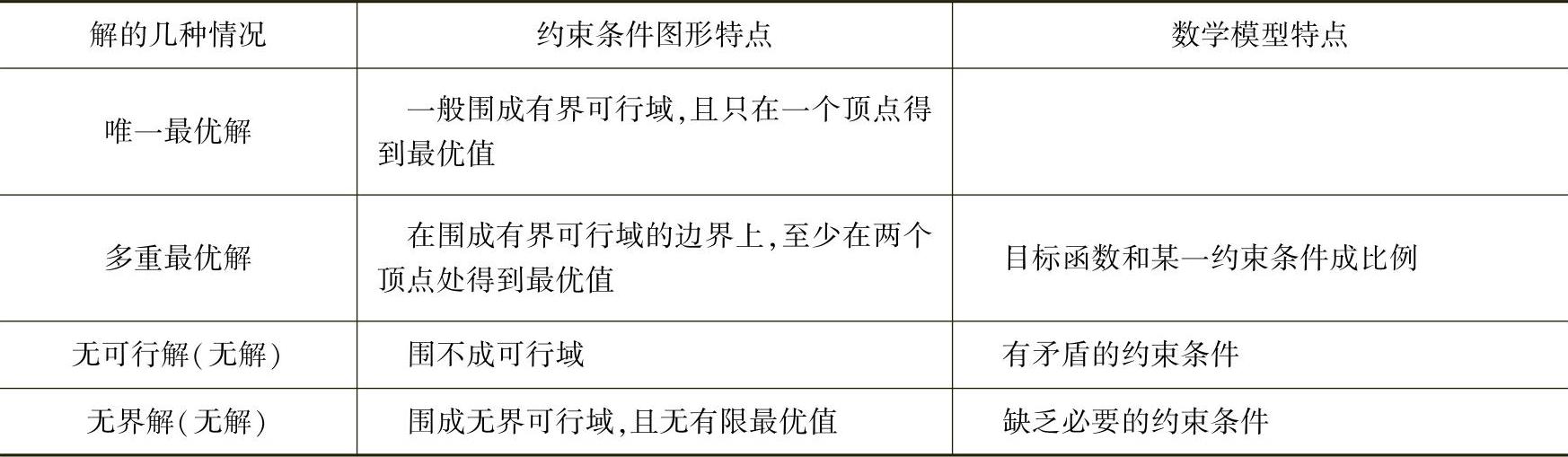
通过以上例题分析，可将图解法得出线性规划问题解的几种情况归纳为如下表1-2所示。

表1-2 线性规划解的几种情况