线性规划（Linear Programming，LP）是在一组约束条件（既定要求）下寻找一个目标函数（衡量指标）的极值。线性规划是运筹学中较为成熟和应用广泛的一个重要分支，计算方法较为成熟，借助计算机可求解众多变量和约束条件的线性规划问题，计算更为方便。下面用实例来说明什么是线性规划问题以及线性规划问题的数学表达式。

在生产管理和经营活动中经常遇到一类问题，即在现有的资源条件下，如何组织安排生产，以获得最好的经济效益（求极大化问题）。

【例1.1】 某工厂在计划期内要安排生产甲、乙两种产品。这些产品需要在设备A上加工，需要消耗材料B、C，按工艺资料规定，生产单位产品所需的设备台时及B、C两种原材料的消耗如表1-1所示。已知在计划期内设备的加工能力为150台时，可供材料分别为300kg、320kg；每生产一件甲、乙产品，工厂可获得利润分别为50元、40元。假定市场需求无限制，工厂决策者应如何安排生产计划，使工厂在计划期内总的利润最大。

表1-1 产品资源消耗

解：这样一个规划问题可用数学语言来描述，即可以用数学模型表示。假设在计划期内生产这两种产品的产量为待定的未知数x₁、x₂，称为决策变量。产品生产得越多，获利就越多，但产量要受到设备和生产能力的限制，这种能力的限制就是约束条件。计划期内设备A的有效台时是150，这是一个限制产量的条件，在安排产品甲、乙产量时，要考虑不得超过设备A的有效台时，这个条件可用不等式4x₁+3x₂≤150来表示；材料消耗总量不得超过供应量，应有7x₁+5x₂≤300，5x₁+6x₂≤320。生产的产量不能小于零，即x₁≥0、x₂≥0，这个条件称为决策变量的非负要求。用Z表示利润，则有Z=50x₁+40x₂，这个式子就是目标函数。该工厂的目标是在不超过所有资源限量的条件下使利润达到最大，即目标函数达到最大值，用数学表达式描述为maxZ=50x₁+40x₂。综合上述，这个问题的数学模型可归纳为：

maxZ=50x₁+40x₂

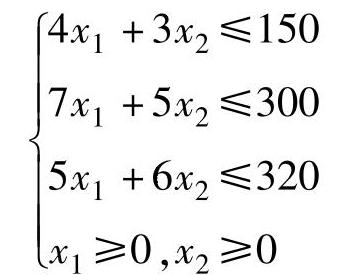
在上面的例题中x_j称为决策变量，不等式组称为约束条件，函数Z称为目标函数。随着讨论问题的要求不同，Z可以是求最大值（如例1.1），也可以是求最小值（如例1.2），因为Z是x_j的线性函数，Z的最大值也是极大值，最小值也是极小值，所以有时也将maxZ与minZ说成求Z的极大值与极小值。

线性规划的数学模型由决策变量、目标函数与约束条件三个要素构成，其特征是：

1）解决问题的目标函数是多个决策变量的线性函数，求最大值或最小值。

2）解决问题的约束条件是一组多个决策变量的线性不等式或等式。

由例1.1可知，一个生产计划问题可用线性规划模型来描述。求出x₁、x₂的值（即最优解），使目标函数达到最大值，就得到一种最优生产计划方案。

此外，线性规划通常也解决资源的最优利用、设备的最佳运行等问题，即在给定目标下，如何统筹兼顾，合理安排，用最少的资源（如资金、设备、原材料、时间等）去实现这个目标（求极小化问题）。

【例1.2】 靠近某河流有两个化工厂（见图1-1），流经第一个化工厂的河流流量为4×10⁶m³/天，在两个工厂之间有一条流量为2×10⁶m³/天的支流。第一化工厂每天排放含有浓H₂SO₄的工业污水2.5×10⁴m³，第二化工厂每天排放这种工业污水1.6×10⁴m³。已知从第一化工厂排出的工业污水流到第二化工厂以前有25%可自然净化。根据环保要求，河流中工业污水的含量应不大于0.2%。因此，这两个工厂都需各自处理一部分工业污水。第一化工厂处理工业污水的成本是1000元/10⁴m³，第二化工厂处理工业污水的成本是800元/10⁴m³。问在满足环保要求的条件下，每厂各应处理多少工业污水，使得这两个工厂总的处理工业污水费用最小。

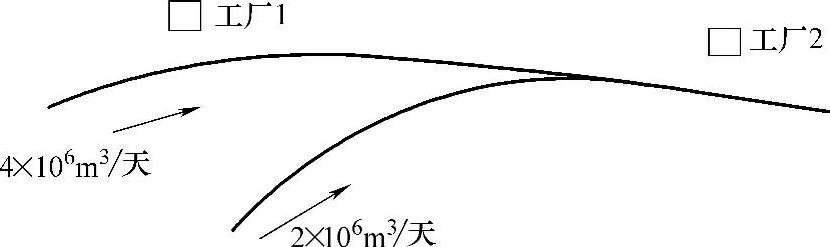
图1-1(www.daowen.com)

解：设x₁、x₂分别为第一个和第二个化工厂每天应处理工业污水的量。

根据河流中工业污水的含量应不大于0.2%的要求，可建立以下不等式：

（2.5-x₁）/400≤2/1000

[0.75×（2.5-x₁）+（1.6-x₂）]/600≤2/1000

由于每个工厂每天处理的工业污水量不会大于每天的排放量，故有：

x₁≤2.5，x₂≤1.6

经整理，得到下列线性规划模型：

minZ=1000x₁+800x₂

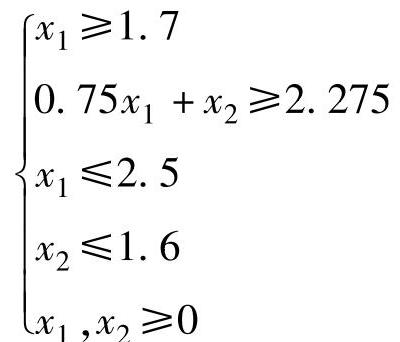
分析上述例题可知：线性规划是研究线性约束条件下线性目标函数的极大值或极小值问题的数学理论和方法；线性规划的数学模型由决策变量、目标函数与约束条件三个要素构成。线性规划数学模型的一般表达式可写成为：

max（min）Z=c₁x₁+c₂x₂+…+c_nx_n

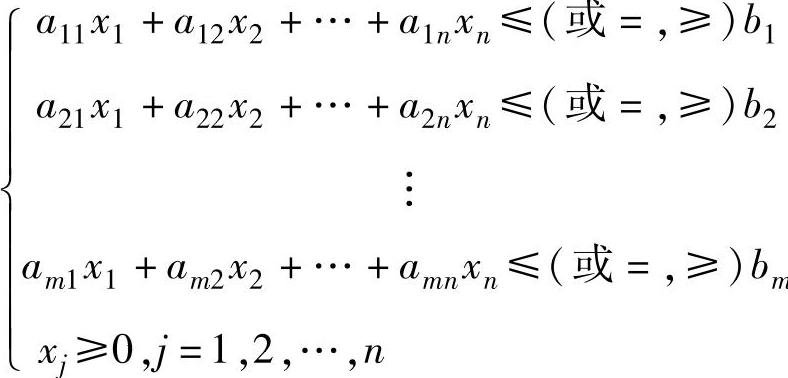
为了书写方便，上式也可写成：

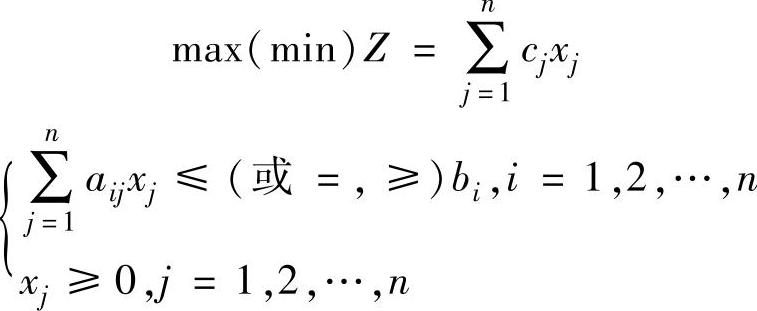
在实际中一般x_j≥0，但有时候x_j≤0或x_j无符号限制。

在线性规划的数学模型中，c_j称为价值系数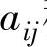，称为工艺系数，b_i称为资源限量。