常见的用于分解混合成本的方法有两大类：定性分析方法与历史成本分析法。

（一）定性分析方法

1.账户分析法

账户分析法也称会计分析法。它根据各个成本项目及明细项目的账户性质，通过经验判断，把那些与变动成本较为接近的划入变动成本，把那些与固定成本较为接近的划入固定成本。至于不宜简单地划入变动成本或固定成本的项目，通过一定比例将它们分解为变动成本和固定成本两部分。账户分析法的优点是简单明了，分析的结果能清楚地反映出具体成本项目，实用价值较高；缺点是分析的工作量大、成本性态的确定较粗。

2.合同确认法

合同确认法是根据企业与供应单位所订立的合同（或契约）中关于支付费用的具体规定来确认费用形态的方法，如电话费、保险费、水费、电费、燃气费等。例如，对于电话费而言，电信公司每月向用户收取的基本费用，可以看成固定成本，按照用户的通话时长计收的费用则是变动成本。合同确认法的优点是成本性态分析比较准确；缺点是其应用范围较小，只限于签有合同生产经营项目的成本的性态分析。

3.技术测定法

技术测定法是根据生产过程中消耗量的技术测定和计算来划分成本的变动部分和固定部分的混合成本分解方法。例如，通过技术测定，把热处理电炉的预热耗电成本（初始量）划归固定成本，把预热后进行热处理的耗电成本划为变动成本。这种方法的优点是划分比较准确；缺点是工作量较大，一般适用于新建企业或新产品的成本性态分析。

（二）历史成本分析法

1.高低点法

高低点法也称两点法，是根据企业一定期间历史数据中的最高业务量（高点）和最低业务量（低点）之差，以及它们所对应的混合成本之差，计算出单位变动成本，进而将混合成本分解为固定成本和变动成本的方法。

由于混合成本包含变动成本和固定成本两种因素，因此它的数学模型同总成本的数学模型类似，也可用直线方程式y=a+bx 来表示。其中，a为混合成本中的固定成本部分；b为混合成本中的单位变动成本；x为业务量；y为成本总额。高低点法的计算公式为

【例6-1】凯达公司2015年上半年的设备维修费与机器的运转小时数的数据如表6-1所示。

表6-1　凯达公司2015年上半年的设备维修费

表6-1中，最高点是5月，业务量为10千机器小时，维修费为230元：最低点是3月，业务量为5千机器小时，维修费为200元。按上述公式计算如下：

反映维修费成本性态的直线方程式为

高低点法分解成本简便易行，有助于管理人员迅速确定成本关系。但这种方法只以诸多历史数据中的最高点和最低点两种情况来取代其他数据，进而确定一条直线，并以该直线代表所有历史数据。如果最高点和最低点是偏离较大的点，它们所代表的可能是非典型的成本与业务量关系，其结果将是不太准确的。

尽管从经济理论上讲，成本函数很少是线性的，通常是二次或三次曲线。但在进行成本性态分析时，我们假设在相关范围内，成本和成本动因之间的关系是线性或近似线性的。

2.散布图法

散布图法是用非数学的方式来辨认某种现象的测量值与可能原因因素之间关系的一种方法。这种方法具有快捷、易于交流和易于理解的特点。物流成本管理中所运用的散布图法，是指将若干期业务量和成本的历史数据标注在业务量和成本构成的坐标图上，形成若干个散布点，然后根据散布点的形成规律来判断业务量和成本之间的相关关系及相关程度，并据此来推测固定成本和变动成本的一种方法。

用来绘制散布图的数据必须是成对的（x，y）。通常用垂直轴表示现象测量值y，用水平轴表示可能有关系的因素x。

根据散布图的形成规律，散布图可分成完全正相关、完全负相关、正相关、负相关、不相关及曲线相关等几种。

（1）完全正相关。x变量增加时，y的变量随着增加，散布点逐渐上升成一条斜线，如图6-8所示。

（2）完全负相关。x变量增加时，y的变量却减少，散布点逐渐下降成一斜线，如图6-9所示。

图6-8　完全正相关

图6-9　完全负相关

（3）正相关。x变量增加时，y变量亦增加，散布点有逐渐上升趋势，如图6-10所示。

（4）负相关。x变量增加时，y变量却减少，散布点有逐渐下降趋势，如图6-11所示。(www.daowen.com)

图6-10　正相关

图6-11　负相关

（5）不相关。当x变量增加时，y的变量并未随之增加，散布点没有上升或下降之趋势，无规律可循，如图6-12所示。

（6）曲线相关。x变量与y的变量之间没有直线相关关系，但却有曲线关系存在，如图6-13所示。

图6-12　不相关

图6-13　曲线相关

运用散布图法的第一步就是将各点画出，以便确定生产成本与业务量的关系。以例6-1中的数据为例，绘制如图6-14所示的散布图。

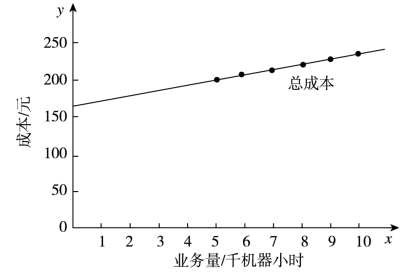
图6-14　凯达公司2018年上半年的设备维修费的散布图

在图6-14中，成本变动趋势直线与y轴的交点，即为维修费用中的固定成本a=165元，单位变动成本b是这条直线的斜率。

反映成本变动趋势的直线方程式为

散布图法利用散布图分解混合成本，综合考虑了一系列观测点上业务量与成本的依存关系，显然，分解的结果较高低点法准确。但散布图的缺陷是选择最佳直线时缺乏客观标准，成本方程式的质量取决于分析者主观判断的质量，有时误差也比较大。

3.回归直线法

回归直线法也称最小平方法，是根据最小平方法原理，从大量历史数据中计算出最能反映出成本变动趋势的回归直线方程式，并以此作为成本模型的一种成本性态分析方法。

回归直线法的数学推导以混合成本的直线方程式为基础，根据这一方程式和实际所采用的一组n个观测值（x1，y1），（x2，y2），…，（xn，yn），即可得到一组用于决定回归直线的方程式：

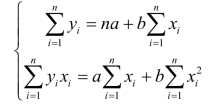
解方程组，得

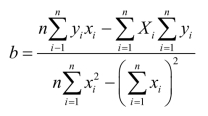
求得b后，即可求a，得

仍沿用例6-1的数据资料，利用回归直线法求解过程如下：

求得

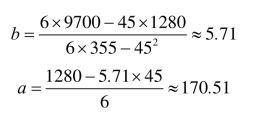
反映维修费成本性态的直线方程为

回归直线法使用了误差平方和最小的原理，相对高低点法和散布图法，其结果更为精确；但其计算过程烦琐，适用于计算机操作。