运输线路的规划是影响运输成本较为关键的一个因素。最佳的运输路线的设计应根据不同客户群的特点和要求，实现车辆高效率运行而且所需车辆最少、运距最短、所需时间最少，从而达到降低运输成本的目的。确定最优运输路线一般可以采取各种数学方法，常用的方法有标号法、表上作业法等。

（一）标号法

在运输线路设计中，当运输起点与运输终点不同时，追求的就是运输距离最短，以节省时间、多装快跑，提高运输的时间效率，这主要是寻求物流网络中的最短路径的问题。其中标号法是确定两点间最短距离的常用方法。

1.标号法的步骤

第一步：给起点V1标号L1=0，表示从V1到V1的距离为0，V1为起点。

第二步：找出与点V1相邻的点中距离最小的一个（若几个点同时达到距离最小就全部找出）。设找出点为Vr并给该点标号Lr=L1+d1r，其中d1r的值为V1到Vr的距离，此时Vr已经标号，同时把V1至Vr的关联边加黑。

第三步：找出与V1、Vr相邻的所有点，把每个已标号的点旁边标注的Lr和与之相邻的点到这个已标号点的距离加起来，从所有结果中选出一个最小值和对应的未标号点，然后给这个点标号，同时把关联边加黑。

第四步：反复上述过程，直到给终点标号，而且相应的关联边加黑为止。

第五步：根据第四步的最小值确定最短路径。

2.标号法的实例

【例4-4】华康物流运输有限公司根据客户指定的地点要求，拟派送一批货物，运送的起点（V1）和终点（V6）、交通网络情况及各区间距离如图4-5所示。请用标号法求出运输的最短路。

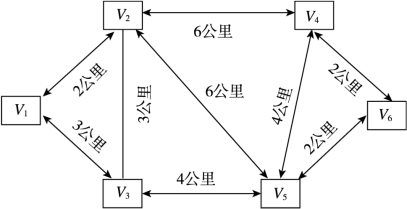
图4-5　运输路线图

依题意可知以下内容。

（1）从V1出发给V1标号L1=0，规划路线图1，如图4-6所示。

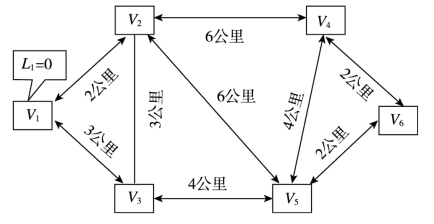
图4-6　规划路线图1

（2）同标号点V1相邻的未标号点有V2、V3，求其最短距：V1-V2距离是2公里，V1-V3距离是3公里；故给其中最小值V2标号：L2=2；将[V1，V2]加黑，规划路线图2，如图4-7所示。

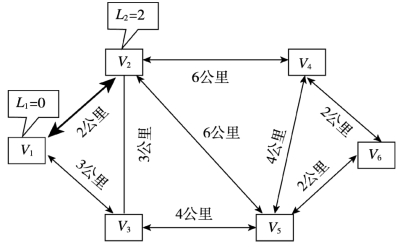
图4-7　规划路线图2

（3）同标号点V1、V2相邻的未标号点为V3、V4、V5，求其最短距离：V1-V3距离是3公里，经V2-V3距离是2公里+3公里=5公里，经V2-V4距离是2公里+6公里=8公里，经V2-V5距离是2公里+6公里=8公里；故给其中最小值V3标号：L3=3；将[V1，V3]加黑，规划路线图3，如图4-8所示。

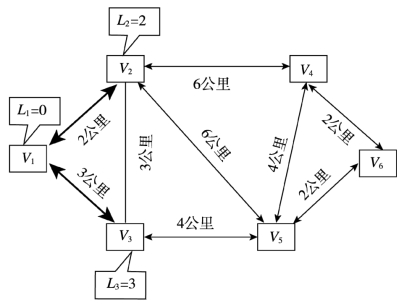
图4-8　规划路线图3

4）重复上述过程，直至给终点标号，关联边加黑，规划路线图4，如图4-9所示。

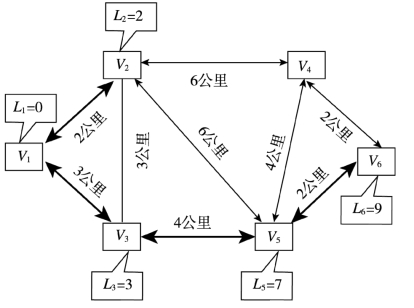
图4-9　规划路线图4

5）通过分析和图示表明从V1点到V6点的最短路径为V1→V3→V5→V6，其最短距离为9公里。

（二）表上作业法

在复杂运输业务中，经常会遇到多个起点和多个终点的问题。多个起点和多个终点的路径优化需要确定各个供应地和各个需求地的最佳供应关系。

多个起点和终点问题的数学模型可以描述为有m个产地Ai，i=1，2，…，m，供应量分别是ai，i=1，2，…，m；同时有n个销地Bj，j=1，2，…，n，需求量分别为bj，j=1，2，…，n，产销平衡；从Aj到Bj运输单位货物的运价（也可以是时间或距离）为cij。那么，如何调运会使总运费（或时间、吨公里）最少？一般情况下，解决这个问题应用到的定量方法是表上作业法。(www.daowen.com)

1.表上作业法的步骤

第一步：建立供需平衡运价表。

第二步：用最小元素法求出初始调运方案。

第三步：用位势法检验初始调运方案。

第四步：用闭合回路法调整初始调运方案。

第五步：重复第三步、第四步，直到出现最优调运方案。

第六步：计算总运费。

2.表上作业法实例

【例4-5】某地区某种粮食作物的3个产地分别是A1、A2、A3，供应量分别是7000吨、4000吨、9000吨。该粮食分别销往B1、B2、B3、B4 4个地区，4个销地的需求量分别是3000吨、6000吨、5000吨、6000吨，产销平衡。请用表上作业法的基本原理设计最优调运方案。

依题意可知以下内容。

（1）建立供需平衡运价表。根据供应地的供应总量、需求地的需求总量及运价情况建立供需平衡运价表，如表4-11所示。

表4-11　供需平衡运价表

（2）用最小元素法求出初始调运方案。应用最小元素法，即优先处理运价最小的供需点，以此类推，最后得出优先供应安排的运量表，如表4-12所示。至此，可得初始调运方案总运费。

表4-12　优先供应安排运量表

（3）用位势法检验初始调运方案。结合上述初始调运方案，应用位势法编制检验表，如表4-13所示。如果检验表中所有数据均为非负，则初始调运方案即为最优方案；如果检验表中存在负数，则说明初始调运方案不是最优解，需要调整。

表4-13　检验表1

（4）用闭合回路法调整初始调运方案。由于表4-13中存在负数，说明该初始方案不是最优方案，需要采用闭合回路法进行调整。经过调整，新的调运方案产生，如表4-14所示。对新的调运方案再次应用位势法进行检验，直至检验表中数字均为非负，如表4-15所示。表4-15中数字均为非负，可见已求得最优解。

表4-14　新的调运方案

表4-15　检验表2

（5）计算总运费。

经过调整，总运费比初始方案总运费86万元节约1万元。最优调运方案为A1向B3运输5000吨，A1向B4运输2000吨；A2向B1运输3000吨，A2向B4运输1000吨；A3向B2运输6000吨，A3向B4运输3000吨。

标号法和表上作业法分别解决了运输中起点和终点不同的问题、多个起点和终点的问题，此外，起点和终点相同的路径规划问题也是物流运输配送业务中常见的问题。在这个问题中，由于要求车辆必须返回起点，难度就提高了。解决这类问题的目标是找出途经的所有点的顺序，且使总出行距离最短。针对这类问题专家已经提出了很多方法，但是随着问题中包含的节点个数和约束条件的增加，求解问题的复杂程度也增加，要找到最优路径非常困难，即使用最快的计算机进行求解，也需要很长时间。目前，启发式求解法（Heuristic Solution）是较为理想的办法，这种算法是相对于最优化算法提出的，它实质上是一个基于直观或经验构造的算法，在可接受的时间和空间范围内，给出待解决组合优化问题的一个可行解，一般情况下该可行解与最优解的偏离程度是不能被预计的，由于该方法涉及很多运筹学和计算机的基本理论，这里就不介绍了。