【参考答案】

（一）单项选择题

1.A 2.C 3.B 4.D 5.A 6.A 7.C 8.A 9.D 10.A

11.C 12.B 13.A 14.C 15.B 16.B 17.B 18.A 19.A 20.B

21.C 22.C 23.B 24.D 25.B 26.C 27.D 28.B

（二）多项选择题

1.ABE 2.ABCD 3.ABCD 4.ABC 5.ABC

6.ACDE 7.ACE 8.BCDE 9.CE 10.ABCE

11.ACE 12.AB 13.ABE 14.ABE 15.ABD

16.BD

（三）判断题

1.× 2.√ 3.× 4.√ 5.× 6.√ 7.× 8.× 9.× 10.×

11.√ 12.√ 13.× 14.× 15.×16.√ 17.×18.×19.√ 20.×

21.√ 22.√ 23.×24.√ 25.×26.√

（四）计算题

1.【解】

该家庭每月用于住房支出的数额A=8000×40%元=3200元

i=6%/12=0.5%

n=10×12月=120月

最高贷款额P=A[（1+i）ⁿ-1]/[i（1+i）ⁿ]

P=3200×[（1+0.5%）¹²⁰-1]/[0.5%×（1+0.5%）¹²⁰]=288235.05（元）

2.【解】

已知银行存款月利率为6%/12=0.5%，n=12，为便于计算，将其换算为复利利率，运用公式i₁=[（1+i₂）ⁿ-1]/n（其中，i₁为单利，i₂为复利），可得银行存款复利月利率为0.487%。

该家庭前5年存款的本息和为：

F=2400×50%/0.487%×[（1+0.487%）^12×5-1]=83389.24（元）

注：该家庭前5年存款的本息和也可用单利求取。

F=2400×50%×12×5+2400×50%×（60+59+58+…+1）×0.5%=1200×60+1200×0.5%×（60+1）/2×60=82980（元）

10年内该家庭可偿还贷款现值为：

P=A₁/（i-s）{1-[（1+s）/（1+i）]ⁿ}（当i≠s时）

贷款月利率i为9%/12=0.75%，s=0.6%

A₁=2400×40%元=960元，n=12×10月=120月

P=2400×40%/（0.75%-0.6%）×[1-（1.006/1.0075）¹²⁰]=104781.50（元）

所以，该家庭有偿还能力的住房价格应控制在：

83389.24（82980）+104781.50=188170.74（187761.5）（元）

住房面积：188170.74（187761.5）/2400m²=78.40（78.23）m²

3.【解】

由公式i=（1+r/m）^m-1得到：12.62%=（1+12%/6）^m-1

即m=6，一年分为6次计息，即该贷款是以两个月计息。

说明：解此题需要一些技巧，不能死套公式。一般来说，计息周期不外乎半年、季度、一个月、两个月、日等固定周期，可用试算法解决。

4.解题思路：先用收益法中净收益按一定比率递增公式算出第一年的净收益（这里是指“年租金”A），再利用年租金每年上涨的公式A_t=A₁（1+s）^t-1可求出任意年份的年租金。

【解】

（1）已知P=400万元，n=20年，i=18%，s=5%，t=8

（2）由A₁=P（i-s）/{1-[（1+s）/（1+i）]ⁿ}可得

A₁=400×（18%-5%）/{1-[（1+5%）/（1+18%）]²⁰}=57.58（万元）

（3）利用公式A_t=A₁（1+s）^t-1，可得A₈=57.58×（1+5%）^8-1=81.02（万元）

该写字楼第8年的净租金收入达到81.02万元以上时，方能满足投资者收益目标的要求。

说明：此题是用计算等比序列现值系数公式来求解，仍可套用收益法中净收益按一定比率递增公式计算，仅需将该公式中的g换成s、Y换成i即可。通过这种对比学习，只要记住收益法中若干公式即可，不用再去记忆教材中有关资金等效值和复利计算的公式，化繁就简，事半功倍。

5.解题思路：据题意是按月等额还款，选用净收益每年不变有限年期公式，将其中的报酬率Y换成i，求出每月等额还款数A。画出现金流量图，将第10年年初看作计息起点0，第10年年末就是1点，以此类推，第15年年末的标记点为6，则t=6×12月=72月，注意t=5×12月=60月的表述是错误的。这也是在教材中一个难点和容易出错的点，一定要注意选对计息期的起点和终点。

【解】

（1）已知P=4500元/m²×120m²×70%=378000元，n=15×12月=180月，t=6×12月=72月，i=12%/12=1%

（2）A=P[i（1+i）ⁿ]/[（1+i）ⁿ-1]=378000×1%×（1+1%）¹⁸⁰/[（1+1%）¹⁸⁰-1]=4536.64（元）

（3）第10年年初拟一次偿还的金额为：

P₁₀=A/i[1-1/（1+i）^t]=4536.64/1%×[1-1/（1+1%）⁷²]=232050.91（元）

第10年年初一次偿还的金额为232050.91元。

6.解题思路：此题由题意分析可知，是要求P值。选用净收益每年不变有限年期公式，将其中的报酬率Y换成i。

【解】

（1）该家庭每月能支付的房款A=6000×30%=1800（元）

（2）n=15×12月=180月，i=6%/12=0.5%

（3）该家庭能承受的抵押贷款额P=A/i[1-1/（1+i）ⁿ]

P=1800/0.5%×[1-1/（1+0.5%）¹⁸⁰]=213306（元）

（4）该家庭能承受的购房总价值V=213306/80%=266633（元）(www.daowen.com)

（5）该家庭的支付能力最多可以购买住宅面积S=266633/3000m²=88.88m²

7.【解】

该家庭用于支付住房抵押贷款的月还款额为：16000×30%=4800（元）

月利率=12%/12=1%

由于月收入为月初，先把其折到月末：4800×（1+1%）=4848（元）

利用公式P=A/i[1-1/（1+i）ⁿ]，求得该家庭有偿还能力的最大抵押贷款额为

P=4848×[（1+1%）¹²⁰-1]/[1%×（1+1%）¹²⁰]=337908.13（元）。

8.【解】

（1）计算该家庭购买住房的最高总价

月还款额：A=7000×25%=1750（元）（0.5分）

最高贷款额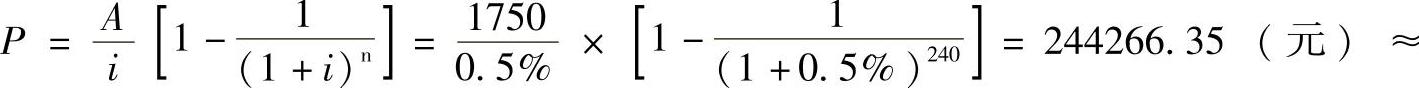：24.43（万元）（1分）

（本步计算中，i取0.5%，n取240，给0.5分）

购买住房的最高总价：24.43/70%=34.9（万元）（0.5分）

（2）计算第6年初一次性提前偿还款

解法1第5年末尚余贷款本金：

（本步计算中，i取0.5%，n′取180，给0.5分）

调息后的月还款额：

（本步计算中，i′取0.75%，n′取180，给0.5分）

调息后每月增加的还款额：2103.40-1750.0=353.40（元）（0.5分）提前还款额：

解法2

设提前还款额为P″，则有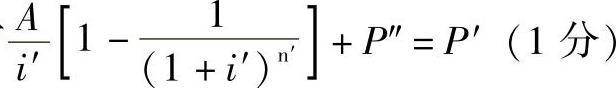

第5年末尚余贷款本金：

（3）贷款延长期的计算

设从第5年末开始的还款期为X月，则有

延长期：294-180=114（月）=9.5（年）（0.5分）

解析

（一）单项选择题

13.名义利率=周期利率×每年的计息周期，此题中名义利率=1%×12=12%。

14.一年计息4次时的实际利率=（1+3%）4-1=12.55%；一年计息12次时的实际利率=（1+1%）^12-1=12.68%

15.用公式I_n=F_n-P计算，I_n=（1+6%/12）^12×3-1=19.67（万元）

16.折现率与利率相等，选用公式P=nA₁/（1+i）计算可得。

22.现值是资金运动起点的金额，终值是资金运动结束时与现值等值的金额。

23.i=（1+12%/4）4-1=12.55%。

24.i=（1+0.625%）12-1=7.76%。

25.月等额还款金额=10×0.7%=700（元），月利率=6%/12=0.5%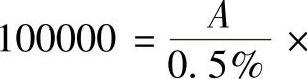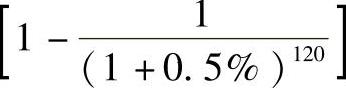，，则A=1110.21元，1110.21-700=410.21（元）。

26.运用公式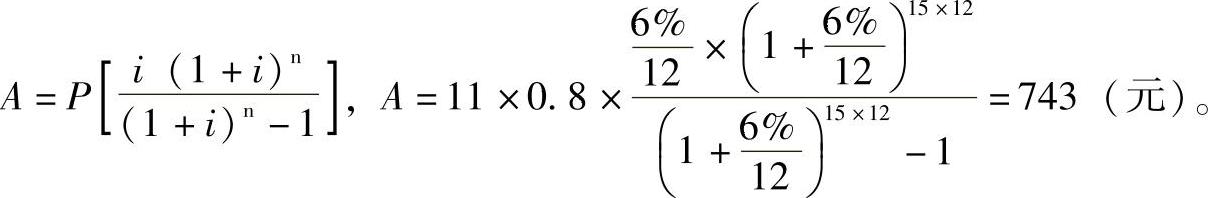

27.20万贷款，28年的贷款期限，利用等额序列支付资金回收系数公式计算可得。

28.将第6年初的5万元看作P，在余下的10年中每月等额还款数就是从第6年开始的抵押贷款月还款额减少值。运用公式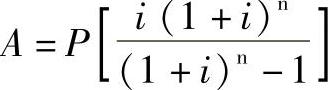可得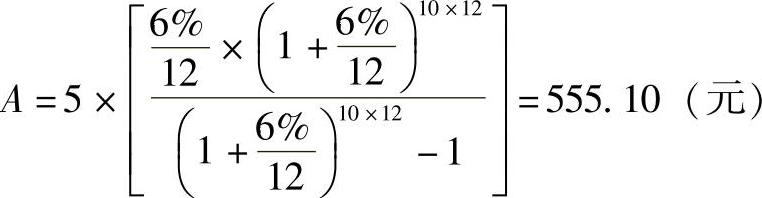：。注意：公式中的n是10而不是9，因为第6年初等于第5年末。做这种题一定要画一个现金流量图。

（二）多项选择题

8.对于房地产开发投资项目来说，现金流出主要包括土地费用、建造费用、还本付息、经营费用、税金等。

12.对于房地产开发投资项目来说，现金流入通常包括销售收入、出租收入、其他经营收入。

16.①实际利率比名义利率更能反映资金的时间价值；②名义利率越大，计息周期越短，实际利率与名义利率的差异就越大；③当每年计息周期数m=1时，名义利率与实际利率相等；④当每年计息周期数m>1时，实际利率大于名义利率；⑤当每年计息周期数m→∝时，名义利率r与实际利率i的关系为i=e^r-1。

（三）判断题

1.名义利率越大，计息周期越短，实际利率与名义利率的差异就越大。

3.从理论上讲，资金在不停地运动，每时每刻都在通过生产和流通领域增值，因而应该采用连续复利计息，但是在实际使用中都采用较为简便的间断复利计息方式计算。

4.资金等值是指在考虑时间因素的情况下，不同时点发生的绝对值不等的资金可能具有相同的价值。

5.资金一旦用于投资，就不能用于即期消费，从消费者的角度来看，资金的时间价值体现为放弃即期消费的损失所应得到的补偿。

7.为了与期末惯例法保持一致，在把资金的流动情况绘成现金流量图时，都把初始投资P作为第0期期末发生的。

8.从投资者的角度来看，资金的增值特性使其具有时间价值。从消费者的角度来看，资金的时间价值体现为放弃即期消费的损失所应得到的补偿。

9.现金流量图中的“0”表示第0期期末。

10.在名义利率不变时，计息次数越多，实际利率越大。

11.运用公式i=（1+r/m）^m-1，在m不变时，名义利率r越大，实际利率i就越大。

13.复利计息还有间断复利和连续复利之分。如果计息周期为一定的时间区间（如年、季、月等），并按复利计息，称为间断复利；如果计息周期无限期缩短，称为连续复利。

15.从理论上讲，资金在不停地运动，每时每刻都在通过生产和流通领域增值，因而应该采用连续复利计息，但是在实际使用中都采用较为简便的间断复利计息方式计算。

17.0点表示始点，基准点，或当前时点。

18.开发—持有出租—出售模式主要适用于写字楼、零售物业、高级公寓等收益性房地产项目。部分政策性租赁住宅、普通商品住宅也可采用这种模式。

20.将更新改造后的收益性房地产持有并出租经营，并在持有经营一段时间后，根据市场状况和企业财务状况将其转售出去，也是部分房地产企业常采用的业务模式。

23.是流动性偏好利率理论。

25.资金运动过程中某一时间点上与现值等值的金额称为时值。