作家兼科学家古尔德有一阵子是我崇拜的角色模范，他曾被诊断罹患致命的胃癌，关于他能活多久，他收到的第一个信息是：这种病的存活期的中位数，约8个月。他觉得这个信息很像《圣经》中的以赛亚（Isaiah）告知希西家王（King Hezekiah）说，赶快在他死前把家整理好。

这种病情诊断，特别是那么严重的病情，会激励一个人拼命做研究，尤其是像古尔德这种多产的作家，总是希望有更多的时间多写几本书。古尔德进一步研究后，发现实情和他最初获取的信息大不相同。主要的差异在于期望（亦即平均）存活期比8个月长得多。他注意到期望值和中位数两者根本不同。中位数意指约50%的人活不到8个月，50%的人则活了8个月以上。但是活了8个月以上的人，生命维持的期间相当长，大致来说和普通人一样，可以活到保险死亡表预测的平均寿龄73.4岁左右。

这就是不对称（asymmetry）现象。活不到8个月的人，很早就死掉了，而活过8个月以上的人，则继续活得更久。结果出现不对称时，存活期平均值和存活期中位数并不相同。古尔德因此发现偏态（skewness）的概念，因而呕心沥血写下《中位数不能传达什么》（The Median is Not the Message）一文。文内的主旨是，医学研究机构使用的中位数概念，不具备概率分布的特性。

我将简化古尔德的论点，以跟疾病没有关系的例子——赌博，来介绍平均数（也称做期望值）的概念。我举的例子会同时提到不对称概率和不对称结果。不对称概率是指每一事件的概率不是50%，而是一边的概率高于另一边的概率。不对称结果是指报酬不相等。假设我参加的赌博，1000次里面有999次赚到1美元（事件A），有一次赔10000美元（事件B），如表6-1所示。

表6-1(www.daowen.com)

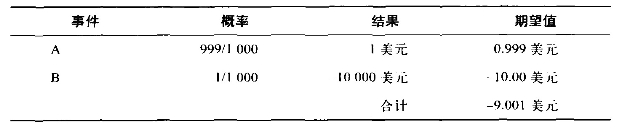
我的期望值是赔9美元左右，这是将概率乘以对应的结果所得到的数字。赔钱的频率或概率本身完全没有用处，它必须和结果的大小一起判断。这里的A发生的概率远高于B。我们如果赌事件A会发生，赌赢的概率很高，但这么做不是好想法。

个中的道理很简单，小赌过的人一定都了解。但是我在金融市场却得费尽力气，和那些怎么想也想不通的人争执不下。这些人并不是新手，而是学历很高如MBA的人，他们却搞不懂其中的差别。

他们怎么会不懂其中的道理？他们怎么会把概率和期望值混为一谈，也就是把概率和概率乘以报酬混为一谈？主要是因为大多数人接受的学校教育、举的例子都是出现在对称的环境中，例如掷硬币时，这种差别就无关紧要。事实上，社会中应用甚广的所谓“钟形曲线”是完全对称的，后面我会再谈这一点。