1.固定效应方法

在产品评论对销量影响的多元回归模型中，存在着难以观测和度量的固定效应变量。同时，多元回归模型中目标解释变量的系数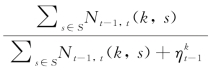还与时间序列相关。因此，为了消除非观测效应对销量的影响，估计可观测变量的系数，本书采用固定效应方法对多元回归模型进行参数估计[124，198]。

固定效应方法通过从模型在各个时段的观测值中减去其组内平均值，以去除一些短时间内不会发生变化的变量对销量的影响。

因此，时间间隔取0～t，对公式（6-18）进行固定效应转换。

其中，表示t时段内新增的产品j属性k及其对应的正、负面评价s，表示t时段内新增的对产品j属性k的平均评价，βk表示消费者对产品属性k的偏好，表示消费者对产品属性k的期望初始值（这里假设消费者群体对产品属性k持有相似的期望，即具有相同的和），Njt（k，s）表示t时段内产品j属性k及其评价s在新增评论中出现的次数，ηk表示消费者对产品属性k的认知强度。

通过固定效应转换，固定效应（Fixed）不再出现在模型中，所以消除了那些难以直接观测和度量的变量对销量的影响。此外，产品类型通常不会随着时间而改变，网络零售商之间存在着长期的竞争关系，其竞争状态在短时期内也不会发生变化。因此，产品类型（Type）和网络零售商的竞争（Competition）等两个控制变量（也是哑变量）在公式（6-19）中都被去除了。

2.估计量的无偏一致性分析

如果面板数据模型中的随机误差能满足以下3个假设，那么模型系数的固定效应估计量是最优线性无偏估计量。

假设3：（严格外生性假设）对每个时段t内，在给定所有时期的解释变量和非观测效应的条件下，误差的期望值是零。

假设4：（等方差假设）在给定所有时期的解释变量和非观测效应的条件下，误差的方差在所有时期都相等。

假设5：（相互独立假设）在给定所有时期的解释变量和非观测效应的条件下，对于所有tm≠tn，误差是不相关的，并且其协方差为0。

除了模型中考虑到的解释变量，还可能存在随时间变化的、被忽略的或者难以观测的遗漏变量。例如，产品广告和促销活动等外部因素可能同时影响产品销量和评论。这些遗漏变量与解释变量相关，从而产生内生性问题，使得随机误差项不满足严格外生性、等方差与相互独立的假设条件，导致OLS估计的不一致。(www.daowen.com)

3.两阶段最小二乘估计法

本章采用两阶段最小二乘法（Two Stage Least Squares，2SLS）进行参数估计。两阶段最小二乘法本质上属于工具变量法（Instrumental Variable，IV），它包括两个阶段：第一阶段，首先是找到一组工具变量，并且分别将模型中的每个解释变量关于这组工具变量进行最小二乘法回归；第二阶段，所有变量的取值采用第一个阶段回归得到的拟合值，然后对原方程作回归，得到的回归系数就是2SLS的估计值。因此，两阶段最小二乘法的估计量是一致估计量。

在产品销量的多元回归模型中（详见公式（6-19）），产品价格Pricejt可能与随机误差项εjt相关，即E（εjt|pjt）≠0。根据龚诗阳等人[109，198]和Archak等人[124-125]的研究，本章将价格的滞后项（即t-1期的价格）当作工具变量。

具体来说，分两阶段计算价格Pricejt的系数α2：第一阶段，把Pricejt分解成两部分，一部分（记作yjt）与随机误差项εjt相关，另一部分（Pricejt-1）与εjt无关，即Pricejt=π0+π1（Pricejt-1）+yjt；第二阶段，利用与随机误差项无关的（π0+π1（Pricejt-1））进行估计。

此外，由于系数，即产品j属性k及其正、负面评价s在新增评论中的权重）依赖于无法确定的参数η，使得模型存在非线性问题。由于，其中为似然函数的方差，所以本章采用最大似然法来估计参数η，也就是将对参数η的估计转换为拟合优度R2的最大化。

4.显著性检验

本书假设产品评论的文本信息对产品销量具有显著的影响，并且不同产品属性的正、负面评价对产品销量具有不同的作用。因此，对该假设进行显著性检验。本章采用F检验方法进行假设检验，其中原假设H0和备选假设H1分别是：

H0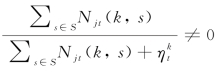：，即产品评论的文本信息对产品销量具有显著影响。

H1：H0不正确。

其中，SSEr表示受约束模型（以产品评论文本信息为解释变量的产品销量模型）的随机误差项平方和，SSEur表示不受约束模型（不包含产品评论文本信息的产品销量模型）的随机误差项平方和，n为样本容量，k+1为不受约束模型的参数个数，q=1。所以，F统计量服从自由度为（q，n-k-1）的随机变量分布。

给定显著性水平（α=1%，5%和10%），若F>Fα（q，n-k-1），则应该在相应显著性水平α上拒绝原假设，即产品评论的文本信息对产品销量的影响在显著性水平α上不显著；反之，则不能拒绝原假设。