1.不确定条件下的消费者购买决策

令产品z=（z1，z2，…，zn），其中zk（k=1，2，…，n）表示用户对产品属性k的评价。此外，消费者由于自身偏好对产品各个属性给予不同程度的重视，所以对不同产品属性的评价进行加权求和，可以得到产品的综合评价，如式（6-1）所示。

其中，Zj为产品j的综合评价，βk为产品属性k在产品价值感知中的权重，Fj为产品j的评价累积分布函数。假定所有消费者共享同一信息集（即阅读同一网站上的产品评论），那么每个消费者都能获得相同的产品评价信息，即Fj（i）（i=1，2，…）具有独立同分布。

即使互联网上有海量的产品评论，消费者对于产品的认识仍然是不确定的。也就是说没有一个产品得到公众一致的意见，对产品的评价总是见仁见智、褒贬各异。因此，消费者对产品的认知是有限的。对于消费者i而言，不能确定产品j的价值，所以又将产品j的评价值表示为Zj˜。

在不确定情况下，假定所有消费者都是风险规避的，但是他们的风险规避程度不同。冯·纽曼·摩根斯坦（von Neumann-Morgenstern）效用函数是一个经常被用于描述风险规避型消费者效用的指数型效用函数，所以用它来描述不确定性对消费者购买决策的影响。因此，消费者在不确定条件下选择产品的效用函数如式（6-2）所示。

其中，b（i）是消费者i的支出预算，pj是产品j的价格，γ（i）是预算与价格对消费者i的边际效用（由消费者的收入决定），β（i）是不同产品属性对消费者i的边际效用（由消费者的偏好决定），β（i）·z～（i）表示边际效用向量与评价向量的内积（即考虑消费者偏好与产品评论的相互影响），εij表示随机误差（比如影响消费者购买决策的随机因素）。通常假设随机误差εij服从正态分布，即εij～N（0，σ2）。

2.消费者认知的贝叶斯学习过程

消费者对产品的认知取决于从产品评论中获得的不同属性的正、负面评价信息。随着产品评论的更新，消费者对产品各个属性的认知也在不断地发生变化。

假设1：考虑到有限的实验数据，假设各个产品属性之间具有相互独立性，不存在相互作用。

根据Roberts and Urban[187]的研究，消费者对不同产品属性的认知服从正态分布，其表达式为对角协方差矩阵。

其中，μkj和分别表示消费者对产品j第k个属性认知的先验分布的期望与方差。

本章采用贝叶斯学习法描述产品评论的更新所引起的消费者认知变化。根据贝叶斯定理，产品属性的评价观点先验分布与后验分布之间存在以下线性关系。

定理1：P（θ|X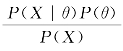）=，其中P（θ）表示先验分布，P（θ|X）表示后验分布，P（X|θ）表示似然函数。

定理2：如果先验分布和似然函数可以使得先验分布和后验分布具有相同的形式，那么就称先验分布与似然函数是共轭的。

在一定正则性条件下，递归的贝叶斯学习过程所得到的后验分布渐近于正态分布。因此，本章选择共轭先验为似然函数，同样也服从正态分布。

由于产品评论中的正面观点和负面观点对消费者认知具有不同程度和方向的影响，其中正面评价可能提高消费者对产品的期望，而负面评价则可能降低消费者的期望，所以需要分别研究产品各个属性的正面观点和负面观点对消费者认知的影响。如果产品j第k个属性的评价为，似然函数的方差为τ2k，并且按照评价的不同情感极性zjk=（xkj1，xkj2）（其中，xkj1表示产品j属性k的正面观点，xkj2表示产品j属性k的负面观点），那么产品j属性k的正、负面评价后验分布如式（6-4）所示。

其中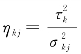，表示消费者对产品属性k的认知强度。如果ηkj=∞，表示消费者已获取关于产品属性k的所有信息，对该属性已有最终的认知，不再受产品评论的影响；如果ηkj=0，则表示消费者对产品属性k毫无概念。(www.daowen.com)

6.2.3.3 消费者的期望效用函数

假定产品各个属性的效用可以叠加，那么消费者i选择产品j的总体期望效用如式（6-5）所示。

定理3：对于产品j和产品l，当且仅当，∀j≠l时，消费者i会选择产品j，即：

或者

其中，

不难看出，消费者的期望效用函数与单调一致，因此可以推出下一定理。

定理4：对于产品j和产品l，当且仅当，∀j≠l时，消费者i会选择产品j。当最大时，消费者选择产品j能获得最大的期望效用。在最大化消费者的期望效用时，采用能够减少不确定因素（包括消费者收入（b（i）），产品价格（pj）以及随机误差（εij）等）产生的影响。因此，又将称作消费者的“风险偏好函数（Risk-adjusted Preference Function）”[187]。

根据6.2.3节的贝叶斯学习，消费者通过浏览产品评论，不断改变其对产品各个属性的认识。所以当新增一系列关于产品j属性k的正、负面评论（xkj1，xkj2）时，消费者的风险偏好函数也会随着发生改变。根据产品属性k的正、负面评价后验分布（详见式（6-4）），可以得到新的风险偏好函数：

4.消费者偏好同质性假设

考虑到计算复杂度以及数据收集上的限制，无法获取每个消费者的偏好信息，也就无法估计产品价格以及不同产品属性对每个消费者的边际效用（即模型中的参数γ（i）与β（i）k（k=1，…，n））。为了便于处理模型，根据相关研究的建模方法[124-125]，本章对消费者的偏好进行同质性假设。

假设2：同一类产品的不同消费者具有相似的偏好。

该假设具有一定的事实依据。由于本章研究的电子产品为水平差异型产品，产品之间的替代性强（即产品属性有限，且不同产品各个属性的性能差异并不明显）。同时，电子产品消费者偏好差异也不显著，大众化程度高。比如对于手机而言，近年来“苹果”一直高居热门手机排行榜首，说明大多数消费者对品牌的偏好成为其购买决策的主导因素。因此，可以对同一类产品的消费者偏好进行同质性假设。

5.消费者对产品的选择概率

由于存在离散的解释变量，并且数量较大，所以本章采用logit模型来近似估计消费者的产品选择概率，这样可以减小计算的复杂度。此外，假设随机误差εij与产品属性无关，并且服从标准Ⅰ型极值分布。因此，消费者选择产品j的概率如式（6-10）所示。

通过对消费者的选择概率积分得到产品的市场占有率，如式（6-11）所示。

其中，H（I）和G（v）分别是消费者收入与偏好的累积分布函数。对于式（6-11）中的复杂积分问题，根据消费者偏好的同质性假设，可以将消费者群体进行归一化处理，从而将产品的销量近似为：