本书使用Gibbs抽样算法估计SA-LDA主题模型的隐含变量π、θ和φ。根据3.2.1节的描述，Gibbs抽样算法首先在每一次迭代时都使用排序方法选取概率向量的一个维度；然后在给定其他维度变量值的条件下，对当前维度值进行抽样；接着不断地迭代直到收敛；最后输出SA-LDA主题模型的参数估计值。具体来说，主要有以下四个步骤。

（1）在初始化阶段，随机给评论中的每个片段分配情感（s=j）和“情感-属性对”（s=j，z=k），对评论片段中的每个词语分配“情感-属性对”（s=j，z=k）。

（2）统计被分配到“情感-属性对”（s=j，z=k）的词语数量，被分配到“情感-属性对”（s=j，z=k）的评论片段数量，以及被分配到情感（s=j）的评论片段数量。

（3）开始迭代直到收敛，循环迭代计算第i个评论片段f被分配到“情感-属性对”（si=j，zi=k）的条件概率。换句话说，根据其他评论片段的“情感-属性对”分配情况，估算当前评论片段被分配到“情感-属性对”（s=j，z=k）的条件概率分布。

（4）当迭代收敛至算法停止时，输出矩阵和，其中表示每个词语归属于“情感-属性对”（si，n，zi，n）的概率分布。

根据以上步骤，先计算SA-LDA主题模型的联合概率分布；再通过贝叶斯公式计算评论片段被分配特定“情感-属性对”的条件概率分布；最后求SA-LDA主题模型的隐含变量π、θ和φ。具体的数学推导过程如下。

1.计算SA-LDA主题模型的联合概率分布

为了便于计算，将联合概率分布分解为三个因子的乘积，并且分别进行求解：

（1）计算

根据3.2.1节中的多项式分布公式（3-5），给定“情感-属性对”，求可观测词语的多项式分布：

可以将式（3-14）理解为相互独立的R×M×N次多项式实验。也就是说，在给定“情感-属性对”（si=j，zi=k）及参数β的条件下，语料库中有R×M×N个词语被观测到，表示在“情感-属性对”（j，k）下词语t出现的次数。

其中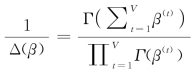，，并且利用了

此外，设定非对称βs以区分不同的情感类型。

（2）计算

同理可得：

其中，

产品评论中的每个片段对应一个产品属性，则有

其中，表示在评论r中被分配到“情感-属性对”（j，k）的片段数量。

其中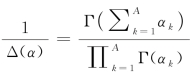，，并且利用了

（3）计算

由于γ是λr的先验参数，而λr是可观察值，所以γ为空值，则有

其中，

其中，表示在评论r中被分配到情感j的片段数量。

其中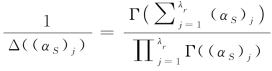，，并且利用了

综合上述，SA-LDA主题模型的联合概率分布为

2.以评论片段为单位，对产品评论进行抽样，并且计算第i个评论片段fr，i被分配到“情感-属性对”（si=j，zi=k）的条件概率

（1）计算

由于评论片段fr，i由词语组成，所以对fr，i的抽样相当于对一组词语进行抽样。

所以，=

下面需要分两步求解：(www.daowen.com)

①不包含第i个评论片段及其词语所在的（si=j，zi=k）项：

②第i个评论片段及其词语所在的（si=j，zi=k）项：；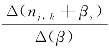

根据①和②，可以得到

其中，表示“情感-属性对”（si=j，zi=k）下的词语数量（不包含当前评论片段中的词语），表示“情感-属性对”（si=j，zi=k）下的词语数量（包含当前评论片段中的词语），并且有为在第i个评论片段中属于“情感-属性对”（si=j，zi=k）的词语数量）。

（2）计算

同理，也分两步求解：

①不包含第i个评论片段及其所在的（ri，si=j）项：

②第i个评论片段所在的（ri，si=j）项：；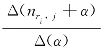

根据①和②，可以得到

其中，表示评论ri中“情感-属性对”（si=j，zi=k）下的评论片段数量（不包含当前评论片段），表示评论ri中“情感-属性对”（si=j，zi=k）下的所有评论片段数量（包含当前评论片段）。

（3）计算

同样分两步走：

①不包含第i个评论片段所在评论ri的项：

②第i个评论片段所在的（ri，si=j）项：

根据①和②，可以得到

其中，表示评论ri中情感（si=j）下的评论片段数量（不包含当前评论片段），表示评论ri中情感（si=j）下的所有评论片段数量（包含当前评论片段），以及在情感（si=j）条件下的先验参数（αS）（j）=αAJ（其中AJ表示情感（si=j）下的产品属性数）。

所以，又可以将式（3-30）转换为

综上所述，第i个评论片段fr，i对应“情感-属性对”（si=j，zi=k）的条件概率为

3.计算隐含变量

计算SA-LDA主题模型隐含的多项式分布变量π、θ和φ。其中，变量π表示评论的情感分布，服从参数为αS的Dirichlet分布；变量θ表示情感s下的产品属性分布，服从参数为α的Dirichlet分布；变量φ表示“情感-属性对”下的词语分布，服从参数为βs的Dirichlet分布。

由于Dirichlet分布共轭于多项式分布，每条评论的情感后验分布、每类情感下的产品属性后验分布以及每对“情感-属性”下的词语后验分布也服从Dirichlet分布。相应的公式如下：

其中，表示评论r中观测到的每类情感出现的次数，是一个S维向量；表示在评论r中观测到的每个产品属性被赋予情感j的次数，是一个A维向量；表示评论r中观测到的每个词语被分配到“情感-属性”（j，k）的次数，是一个V维向量。

根据Dirichlet分布的期望，即，可以推导出评论r表达情感j的近似概率，评论r中的产品属性k表达情感j的近似概率，以及词语t属于“情感-属性对”（j，k）的近似概率分别为

其中，表示评论r中表达情感j的评论片段数量，表示评论r中描述“情感-属性对”（si=j，zi=k）的评论片段数量，表示评论r中归属于“情感-属性对”（si=j，zi=k）的词语数量。

综合上述，SA-LDAGibbs算法可以分为初始化、运算和抽样三个阶段。该算法的实现过程如下。

算法3.1 SA-LDA Gibbs（，α，β，λ，S，A，I）

输入：产品评论以片段向量表示{f→}，片段又以词语向量表示，模型超参数α和β的初始值，情感向量，情感数量S，属性数量A，抽样迭代次数I

输出：模型变量和，超参数α和β的估计