1.LDA主题模型的基本概念

LDA主题模型是一种基于贝叶斯概率的生成模型，最早由Blei等人[129]提出。生成模型和判别模型是属于自然语言处理的两大推断模型。其中，判别模型在建模的过程中不需要关注联合概率分布；而生成模型在获取联合概率分布之后，可以通过贝叶斯公式得到条件概率分布。因此，生成模型所产生的信息比判别模型更丰富，并且生成过程也更容易理解。

LDA主题模型的生成过程是一个无监督学习过程，不需要含有分类标记的样本集。该模型能够对样本数据中的特征项集所属类别的概率参数进行估计，进而利用生成的参数模型进行聚类或者分类等。但是，这一过程导致LDA主题模型的分类结果无明确的指定名称，需要人为地定义挖掘出的主题。

为了将LDA主题模型应用到文本挖掘领域，通常会采用“词袋”（Bag of Word，BOW）理论来表示文本，也就是将非结构化的文本转化为结构化的特征项集[130]。在“词袋”理论的假设中并不考虑自然语言的语法及语序，而是将文本当作一个词语的集合，而这些词语就是该文本中离散的特征项集。在LDA主题模型中，每个词语都可以对应到某个或某几个文本主题。

2.LDA主题模型的原理

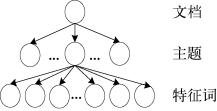
图3-2　LDA主题模型的拓扑结构图

LDA主题模型是一个生成性的三层贝叶斯模型，分为文档、主题和词语三层。其中，一篇文档可对应一个或者多个主题，一个主题对应一个词语表。LDA主题模型的生成过程基于以下假设：语料库中所有文档均按照一定比例由潜在主题混合而成，而主题则是由一系列相关词语混合而成[130]。LDA主题模型的拓扑结构如图3-2所示。

基于LDA主题模型的文本挖掘是生成模型的逆向过程，其贝叶斯网络图解如图3-3所示[129]。其中，实心圆形（wn）表示可观测的随机变量，空心圆形（α，θd，zn，β，φ）表示变量，箭头表示条件概率，方框表示贝叶斯概率求解的迭代过程，N表示词语层，M表示文档层，K表示主题层。

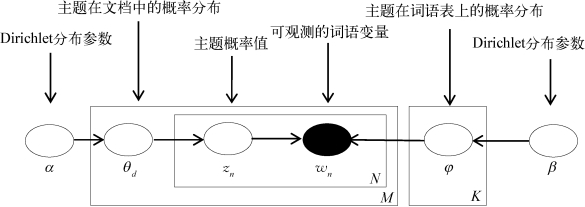
图3-3　LDA主题模型的贝叶斯网络图解

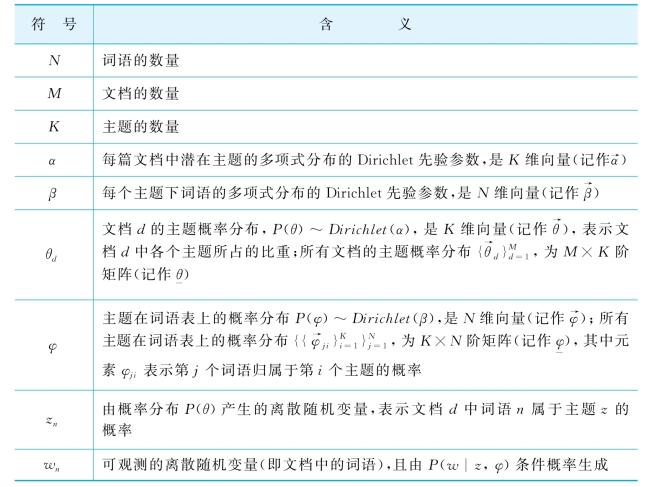
在图3-2中，各个符号的含义如表3-1所列。

表3-1　LDA主题模型的贝叶斯网络图解中符号的含义

综上所述，基于LDA主题模型的文档生成过程如下：

对于每篇文档：

1.生成文档长度N，即文档中词语的个数，且N～Poisson（ξ）；

2.根据Dirichlet分布计算每篇文档中主题分布概率向量；

3.对于每篇文档中的每一个词语wn：

（1）从主题分布概率向量的多项式分布中随机筛选主题zn，即根据分布生成zn，且；

（2）从上述筛选的主题zn的多项式分布中挑选一个词语wn，即根据分布生成wn，且wn～Mult（φzn）；

（3）重复（1）和（2），依次迭代生成剩余的词语。

根据上述生成过程，给定α和β，LDA三层模型的联合概率分布为

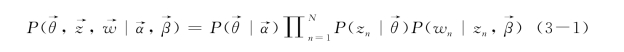
其中，

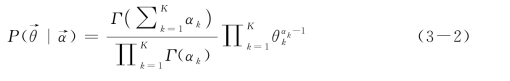
通过加总zn以及对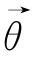积分，得到每篇文档的概率分布：

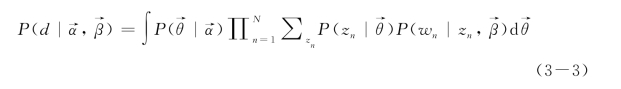
再通过累积每篇文档的概率分布，得到整个语料库的概率分布：(www.daowen.com)

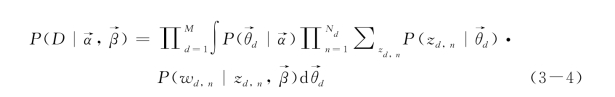
3.LDA主题模型的两种概率分布

多项式分布（Multinomial）和狄利克雷分布（Dirichlet）是概率生成模型中两种常用的概率分布。其中，Dirichlet分布共轭于多项式分布，并且由Dirichlet分布产生的随机数组之和为1。

在LDA主题模型中，文档中词语的主题服从多项式分布，其先验分布选取共轭先验，即Dirichlet分布；每个主题下的词语也服从多项式分布，其先验分布也选取共轭先验，即Dirichlet分布。也就是说，Dirichlet分布主要用于描述“文档（M）-主题（K）”层面的概率分布。

多项式分布的分布概率为

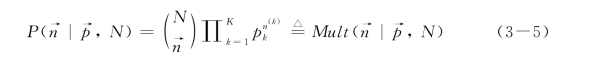
从公式（3-5）中可以看出，多项式分布来自N次独立重复实验，并且每次实验可能有K种结果。在式（3-5）中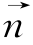，表示实验结果向量，N表示实验次数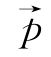，表示出现每种实验结果的概率组成向量，n（k）表示在N次实验中第k种结果出现的次数，多项式系数。

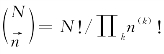Dirichlet分布的分布概率为

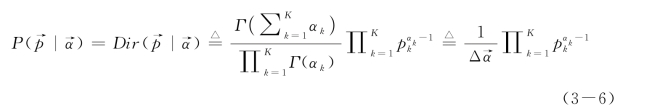
其中，

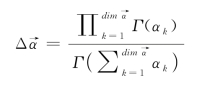
在式（3-6）中，Γ（x）是伽马（Gamma）函数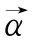，是Dirichlet分布的超参数（Hyperparamer），Δ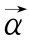是Dirichlet分布的Delta函数。

4.LDA主题模型的求解——Gibbs抽样

在第i篇文档中词语t出现的概率为

整个语料库的似然函数为

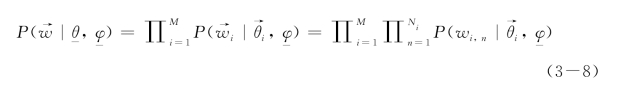
从式（3-7）和式（3-8）中可以看出，LDA主题模型的关键参数是文档-主题分布向量θ和主题-特征词分布向量φ。然而，对于这两个参数的求解是一个非常复杂的最优化问题，很难直接计算，所以需要通过近似推导的方式得到LDA主题模型的近似估计结果。常用的逆向求解联合分布概率的方法主要有两个：Blei等人[129，131]采用的变分贝叶斯期望最大化算法（Mean-field Variational Expectation Maximization）；Griffiths等人[133]和Ramage等人[134-135]使用的Gibbs抽样算法（Gibbs Sampling）。与Blei采用的算法相比，Gibbs抽样算法虽然在效率上稍差些，但是容易实现而且更易于理解。

Gibbs抽样算法是基于马尔科夫链蒙特卡尔理论（Markov Chain Monte Carlo，MCMC）。MCMC是一种复杂的、从概率分布中抽取样本值的近似迭代方法。它允许马尔科夫链先收敛于某个目标分布，再从目标分布中抽样，最后计算得到变量结果。马尔科夫链根据变量赋值的不同而建立不同的状态，并且状态之间的转换遵循着简单的规则[133]。

Gibbs抽样算法构造一条收敛于某目标概率分布的马尔科夫链，并从马尔科夫链最终的状态中抽取被认为最接近于该概率分布值的样本。因此，Gibbs抽样算法的关键是确定LDA主题模型中的目标概率分布。首先，初始化马尔科夫链的第一个状态；然后不断地在当前的马尔科夫链状态上，根据概率分布的情况来抽取所有变量值，从而转换到马尔科夫链的下一个状态；最终，马尔科夫链状态变化很小，趋近于目标概率分布，可以从最后一个状态中得到变量结果。

为了得到文档中的主题概率分布，Gibbs抽样算法并没有直接计算θ和φ，而是通过计算词语w对于主题z的后验概率P（w|z），间接地计算θ和φ的值。对于LDA主题模型，仅仅需要将词语分配到各个主题，即对变量z在词语表上进行抽样，其计算公式如下：

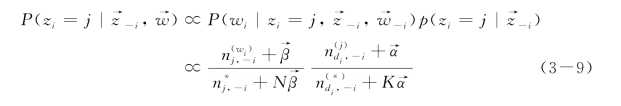
其中，z-i表示除了主题zi=j之外的其他所有主题。表示词语wi被分配到主题j的次数，表示被分配到主题j的词语数量（不包括当前位置的词语），表示文档di中被分配到主题j的词语数量，表示文档di的词语数量（不包括当前位置的词语）。因此，又有和成立。

LDA主题模型利用Gibbs抽样算法进行建模的过程如下：

（1）对语料库中每篇文档的每个观测词w，随机赋予一个主题zi（i=1，…，N）（zi∈{1，2，…，K}），形成马尔科夫链的初始状态；

（2）重新扫描语料库，针对每个词语w，按照式（3-9）重新对主题zi进行采样，更新马尔科夫链i；

（3）迭代步骤（2）足够多次，直到马尔科夫链收敛于目标概率分布，记录zi的当前值，按以下公式估算θ和φ的值：

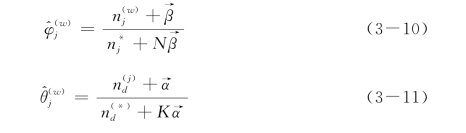
统计语料库的主题-词频矩阵，即文档的LDA聚类结果。