MGWR模型的解释能力为76.6%，略微高于GWR模型的75.7%，因此，MGWR模型能够更好地反映住宅价格与各类住宅特征之间复杂的空间关系。

（1）全局变量分析

从表6.8可以看出，小区环境、邻近大学、运动设施质量、物业管理四个全局变量的回归系数的t值总体都较大，都大于10%显著性水平对应的临界值1.648。其中，小区环境、邻近大学、运动设施质量达到了5%显著性水平。这说明上述四个住宅特征对住宅价格存在较为显著的线性影响。

将GWR模型回归结果中达到5%显著性水平的样本点的回归结果进行统计，可以发现小区环境、运动设施质量、物业管理三个变量的回归系数的均值分别为0.06、0.05、0.04，但它们在数值上的变化幅度并不大，标准差分别为0.015、0.011、0.006。图6.5是根据GWR模型回归结果中邻近大学的回归系数表现显著的样本点所绘制的柱形图，邻近大学回归系数主要分布在0.06与0.12之间。因此，总的来说，在这四个住宅特征对住宅小区价格产生影响的范围内，这种影响在空间上分布相对较为均匀。由此可见，GWR模型的回归结果与MGWR模型空间异质性检验的结果基本一致。

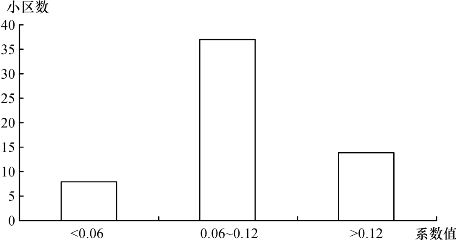
图6.5　邻近大学的回归系数柱形图

具体来看，小区环境是购房者在选房时较为看重的住宅特征，理论上来说，良好的小区环境能给小区带来明显的增值，这在前面的地理加权回归模型中得到了验证。MGWR模型结果显示，小区环境的回归系数为0.048，且达到了1%显著性水平，这说明小区环境直接影响小区住宅的价格，平均来看，小区环境等级每提高一个等级，住宅价格便会增加4.8%，这说明购房者对小区环境具有较大的关注度。此外，小区环境对住宅价格的影响在空间上具有平稳性，这种影响在空间上不存在显著的差异。

线性回归模型结果显示，邻近大学回归系数为0.046，且其显著性水平达到1%，这证明了大学对其周边小区的住宅价格存在显著影响。GWR模型显示，显著样本点中86.4%的样本点回归系数为正，这说明邻近大学和住宅价格之间存在较为明显的正相关关系。而MGWR模型结果表明，邻近大学的回归系数为0.040，且也达到了1%显著性水平，这再次证明其对住宅价格有较为显著的提升作用，但是这种影响在空间上相对恒定。

随着生活水平的提高，越来越多的人意识到适度运动的重要性。线性回归模型结果表明，运动设施质量和住宅价格存在显著的正向线性关系。小区运动设施越完善，质量越好，则小区的住宅价格越高。据GWR模型结果，达到5%显著性水平的样本点的运动设施质量回归系数均大于0，这与线性回归结果相符。MGWR模型结果也揭示了运动设施质量和住宅价格之间的正向关系，且这种关系在空间上的分布较为均匀。

物业管理变量考察的是小区的综合管理水平，正常而言，其对住宅价格的影响应当是正向的。线性回归显示：小区的物业管理水平每提高一个等级，住宅价格平均提高的幅度达到了4.2%。MGWR模型的回归结果表明，物业管理的隐含价格在空间上较为一致，这表明随着我国物业管理的不断规范化以及人们整体素质的提升，大部分小区的物业管理服务都较好，小区之间不存在较为显著的差异。

（2）局部变量分析

前面小节提到在MGWR模型拟合前，GWR 4.0软件的空间异质性检验能够筛选出局部变量，为了更严格地验证筛选出的九个局部变量对住宅价格的影响在研究区域上是否真的存在统计意义上的显著变化，本研究采用Leung等（2000）提出的统计检验的方法。

利用F检验进行以下假设检验：

①H0：β1k=β2k=…=βnk，对任意k成立；

②H1：不是所有的βik都是相等的（i=1，2，…，n）。

构造统计量，即估计值的样本方差，它反映了给定参数的空间变异情况，一个近似的F分布可以用来判断哪个假设是正确的（Leung，2000）。当所得的F值较大时，表明假设H1是正确的，即相对应的参数存在较为显著的空间差异性；反之，假设H0是正确的，即相对应的参数不存在显著的空间差异性。

局部变量F检验值如表6.10所示。统计检验的结果表明，九个局部变量中，只有武林距离、西湖距离以及钱江新城距离三个变量存在显著的空间差异性。因此，我们对三中心隐含价格的空间异质性进行进一步的分析与讨论。

表6.10　局部变量F检验值

①西湖距离隐含价格分析

西湖作为杭州最著名的旅游景点，理论上来说，能够为其周边的住宅以及商业体带来巨大的正向效应。对MGWR结果进行处理，将所有样本点分为四类，即西湖距离达到1%显著性水平、5%显著性水平、10%显著性水平以及不显著，筛选出后，利用GIS得到西湖距离显著性分布图（见图6.6）。从图中可以看到，绝大多数样本点是显著的，可见，西湖对杭州小区的住宅价格的影响范围较大。图6.7给出的是所有样本点西湖距离回归系数分布图。除了少数几个样本点外，基本上所有回归系数为负值，这说明随着小区离西湖的距离的增加，其住宅价格呈现出逐渐下降的趋势，西湖对住宅小区的价格呈现显著的影响（温海珍等，2012）。此外，由表6.9可知，西湖距离回归系数的下四分位值和上四分位值虽然为同向的，但是其变化的强度达到了64.8%。可见，西湖对周边住宅的价格的影响随着空间位置的变化而变化。而图6.7则反映了更多的信息，从图中可以清楚地看出，若剔除不显著的样本点，西湖北面样本点的回归系数绝对值整体上要明显大于其东面样本点的回归系数，这表明西湖北面住宅小区的价格受西湖的影响要明显大于其东面住宅小区所受影响，这与前面GWR模型得到的回归结果较为相似。因此，MGWR模型的结果再次验证了西湖对杭州住宅价格的影响不是均匀的，而在空间上存在明显差异，从而表明传统模型的估计会存在一定的偏差。

(www.daowen.com)

图6.6　MGWR模型西湖距离显著性分布

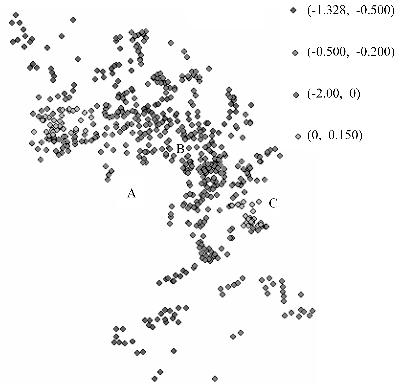
图6.7　MGWR模型西湖距离回归系数分布

②武林距离隐含价格分析

武林广场（图6.9中的B），作为杭州传统的商业中心，是杭州市目前最繁华的中心广场，周围有杭州大厦、杭州剧院及杭州百货大楼等建筑。此外，随着近几年西湖文化广场的开发与运营，武林广场对住宅价格的影响不言而喻。对GWR模型结果中达到5%显著性水平的样本点进行统计，发现武林广场的回归系数分布在-1.259到1.159的范围内，可见其具有明显的空间差异性。因此，MGWR模型的空间异质性检验将武林广场定义为局部变量与事实较为相符。图6.8（a）和6.8（b）是根据GWR模型和MGWR模型中显著样本点的武林距离回归系数绘制的频数直方图。

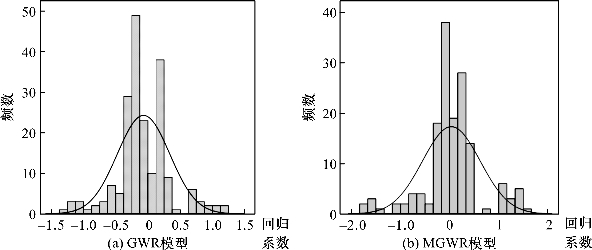
图6.8　GWR模型和MGWR模型武林距离回归系数直方图

由图6.8给出的两种模型回归系数直方图可知，绝大多数样本点的回归系数在-0.5和0之间，GWR模型和MGWR模型结果给出的武林广场对住宅价格的影响较为类似，两者都反映出武林广场对住宅价格的影响大小有着明显的空间差异。图6.9是武林距离显著性分布图，可以明显地看出大多数的样本点是不显著的，且并无整体上的分布规律。可能武林广场在地理位置上处在西湖和钱江新城两个CBD的中间，加上其北面运河的存在，使得武林广场对杭州小区住宅价格的影响呈现较为复杂的分布。

图6.9　武林距离显著性分布

图6.10　武林距离回归系数分布

图6.10是武林距离回归系数分布图，不同区域的住宅小区所受到的影响并不相同。武林广场对其东向、南向以及西向的住宅小区存在较为显著的影响，而且位于武林广场西面的住宅小区受到的影响大于东面以及南面小区所受的影响，可能的原因包括：武林广场东面以及南面的住宅小区自身地理位置已然较为优越，且老小区较多，加上周边配套设施较为完善，东面以及南面住宅小区的价格较为稳定，价格弹性不大；而武林广场以西的小区以新建楼盘居多，武林商圈对其的吸引力相对大于东面以及南面的小区。此外，从系数图上看，武林广场北面小区以及西湖南面的系数以正值居多，这与前面GWR模型的结果基本一致，说明武林广场对北面小区的住宅价格影响不大，这个解释与前面GWR模型的结果一样，可能是由于此区域存在大运河，大运河对住宅小区价格的影响强于武林广场对其的影响，从而导致武林广场的回归系数在此区域为正值。而西湖南面的住宅小区回归系数为正值是由于其与武林广场的距离较远，受到的影响可以忽略不计。

③钱江新城距离隐含价格分析

图6.11　钱江距离显著性分布

钱江新城（图6.11中的C）位于杭州城区的东南方向，是以杭州市商务中心为目标进行开发的，集行政办公、金融、贸易、信息、商业、旅游、居住等功能于一体，将成为杭州新的CBD，其对周边住宅价格的影响显而易见。图6.11揭示了钱江新城距离的显著性情况，虽然从局部看有些无规律，但是从总体上看还是呈现一定的分布特点：显著的样本点主要集中在西湖东南面的住宅小区以及滨江区的小区，其余区域绝大多数样本点是不显著的。这表明钱江新城对杭州住宅小区价格的影响是区域性的，只对局部地区的住宅小区存在溢价效应。可能的原因包括：城西以及城北的住宅小区与钱江新城的距离较远，因而其住宅价格几乎不受到钱江新城的影响；位于主城区的住宅小区受到西湖的影响更大，从而弱化了钱江新城对主城区住宅小区的影响。此外，紧挨钱江新城的几个样本点并不显著，这可能是因为这个区域新建小区居多，且住宅价格普遍较高，人们在购买此区域住宅的时候，考虑更多的是这个区域毗邻钱塘江，且住宅自身质量定位较高。

在不考虑不显著的样本点的前提下，钱江距离隐含价格的分布规律在总体上呈现以钱江新城为中心，其绝对值向外逐渐增大的趋势，这表明离钱江新城越近，价格梯度越缓，钱江新城附近显著样本点的回归系数区间主要为（-0.200，0），随着到钱江新城距离的增加，价格梯度逐渐增加，系数分布区间主要在（-0.500，-0.200）和（-1.594，-0.500）。可见，钱江新城对其周边住宅小区价格的影响，随着空间位置的变化有着显著的变化。

图6.12　钱江距离回归系数分布

与GWR模型不同的是，MGWR模型能够通过空间异质性检验，筛选出隐含价格在空间上较为平稳的住宅特征和具有明显空间异质性的住宅特征。在此基础上，再通过回归得到这两类住宅特征的回归系数，从而能够更好地揭示各住宅特征对住宅价格影响的空间差异性。从表6.9中可以清楚地看到，九个局部变量的回归系数在空间上有着明显的差异，只有西湖距离、小区房龄的系数的下四分位值和上四分位值为同向的，但是其变化的强度也分别达到了64.8%和73.5%；武林距离、钱江距离、公交线路、自然环境、生活配套、教育配套、邻近地铁等七个变量回归系数的下四分位值和上四分位值均为异向的。可见，若仅用传统线性回归模型得到的住宅特征的隐含价格来解释其对住宅价格的影响与实际情况，可能存在较大的差异，GWR模型和MGWR模型能够较好地展现各类住宅特征隐含价格的空间异质性，而MGWR模型获得的结果与实际更相符合。