由于现实中住宅市场往往会受到各种区域性的政策以及其他相关社会经济关系等的影响，并不是所有的自变量对因变量的影响在空间中都存在较为明显的变化，因此采用地理加权回归模型来分析隐含价格的空间异质性时，可能存在一定的偏差。

（1）混合地理加权回归模型的构建

混合地理加权回归（MGWR）模型，是自变量中包含全局变量和局部变量的一种地理加权回归模型。在模型设定时，把那些自变量中对因变量影响较为恒定、不存在显著的空间变化的自变量列为全局变量，其余的列为局部变量。

MGWR模型的构建如下：

式中，lnPi为因变量，即小区i住宅价格的对数，Xij为第i个样本点的第j个自变量（住宅特征），βj（ui，vi）为自变量的回归系数，ui、vi为样本i的地理区位坐标，εi为随机误差项。βj（j=0，1，…，q）为未知的常数，对应着模型中的全局变量。βj（ui，vi）（j=q+1，q+2，…，p）为第i个样本点的未知参数，对应着模型中的局部变量，是（ui，vi）的任意函数。

（2）模型变量的空间异质性检验

混合地理加权回归模型与普通地理加权回归模型的主要区别在于混合地理加权回归模型在回归时，要确定哪些变量属于全局变量，哪些变量属于局部变量。变量的选择直接关系到模型的拟合效果，因此必须采取较为准确可靠的方法来筛选全局变量和局部变量。(www.daowen.com)

在GWR 4.0中，筛选全局变量的方法如下：在判断第k个自变量是否该列为全局变量时，首先进行普通地理加权回归模型，即把所有自变量均视为局部变量进行回归，得到第一次回归结果；然后，把这第k个自变量列为全局变量，把其余自变量列为局部变量，再次进行回归，得到第二次回归结果；接着，把第一次回归结果和第二次回归结果进行比较，如采用AIC准则进行判断，若第一次的回归结果更优，则表明应把第k个自变量列为局部变量，反之，应把第k个自变量列为全局变量；最后，重复上述操作，直到全部的自变量被判断结束，这样就产生了所有的全局变量和局部变量。

（3）混合地理加权回归模型的结果

经过空间异质性检验后，最终检验出13个自变量中九个为局部变量，分别是西湖距离、武林距离、钱江距离、小区房龄、公交线路、自然环境、生活配套、教育配套、邻近地铁；其余的四个变量为全局变量，分别是小区环境、邻近大学、运动设施质量、物业管理（见图6.8和图6.9）。

表6.8　全局变量回归结果

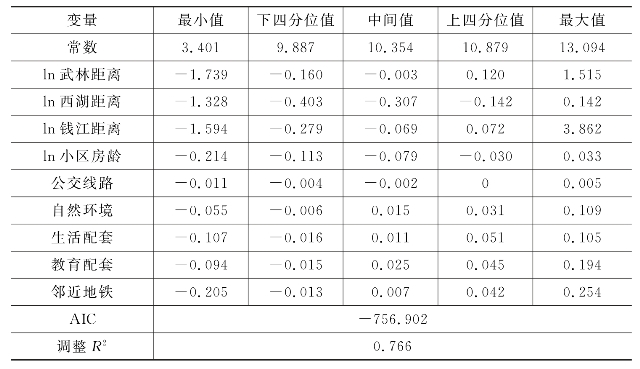
表6.9　局部变量回归结果