（1）显著性分析

表6.4给出了GWR模型回归系数估计的结果，其调整R2达到了0.757，明显高于特征价格模型的调整R20.567，说明相比于特征价格模型，GWR模型能够更好地解释住宅价格与13个解释变量之间的关系。根据t分布表可知，当n=500时，10%显著性水平对应的t值为1.648，5%显著性水平对应的t的临界值为1.965，即当自由度为500时，t的绝对值大于等于1.648，该变量达到了10%显著性水平，当t的绝对值大于等于1.965，该变量达到了5%显著性水平。而本研究的样本数量为603个，则当回归系数对应的t的绝对值大于等于1.648时，该变量也达到了10%显著性水平，当回归系数对应的t的绝对值大于等于1.965时，该变量也达到了5%显著性水平。GWR 4.0的回归结果中提供了每一个样本点各住宅特征回归系数的t值，因此可以根据临界值来判断各变量即各住宅特征回归系数的显著性情况。GWR模型结果中各住宅特征回归系数的显著性样本点所占比例如表6.5所示。

表6.5　10%和5%显著性水平样本点所占比例

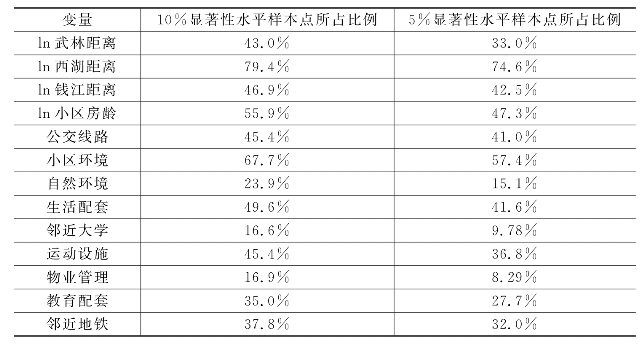
从该表可以看出，并不是所有样本点的回归系数都是显著的。一些住宅特征的回归系数在绝大多数空间位置显著，如79.4%的样本点的西湖距离达到了10%显著性水平，67.7%的样本点的小区环境达到了10%显著性水平，47.3%的样本点的小区房龄达到了5%显著性水平；而部分住宅特征只在少部分空间位置上表现显著，如15.1%的样本点的自然环境达到了5%显著性水平，16.9%的样本点的物业管理达到了10%显著性水平。

将GWR模型的回归结果与特征价格模型的结果对比，可以发现小区环境、自然环境、邻近地铁和小区房龄四个变量在特征价格模型中表现为不显著。然而GWR模型结果却表明这些变量并不是不影响小区的住宅价格，只是它们仅影响某些空间位置的住宅小区的价格。由前面线性回归模型的结果可知，小区环境在特征价格模型中没有达到10%显著性水平，表明总体上小区环境对杭州小区的住宅价格不存在显著的影响。但是，若对GWR模型回归得到小区环境达到5%显著性水平的样本点进行统计，可以发现这些样本点的小区环境的隐含价格均值达到0.061。这表明这些小区的购房者愿意为小区环境提升一个等级而额外支付相当于住宅价格6.1%的费用。由此可见，若仅从特征价格模型结果推出小区环境对住宅价格不存在明显的正向影响，可能与实际情况并不相符。

由上面的分析可以看出，同一住宅特征的回归系数在不同空间位置上的显著性情况并不相同，一些住宅特征在某些空间位置上对住宅价格有显著影响，而在另一些空间位置上对住宅价格的影响可以忽略不计，这表明住宅特征的隐含价格在空间上并不是一致的，而存在空间异质的情况，这也再一次验证了普通特征价格模型平均估计存在的缺陷之处。

（2）影响因素分析

从表6.4给出的GWR模型的回归结果可以看出，同一住宅特征对住宅价格的影响在空间上并不是绝对均匀的，存在一定程度上的差异。这种差异性部分是系数大小的差异，有些则是系数在影响方向上的改变。如西湖距离回归系数的下四分位值为-0.421，而其上四分位值则为-0.171，这意味着在一个空间位置上，到西湖的距离每增加1%，住宅价格便下降0.421%，而在另外一个空间位置上，到西湖的距离每增加1%，住宅价格便下降0.171%，变化的幅度达到了59.4%；生活配套回归系数的下四分位值为-0.017，而其上四分位值则为0.047，这表明生活配套这个特征对住宅价格的影响在两个空间位置上起到了完全相反的作用，类似的变量还有武林距离、钱江距离、邻近地铁等。

由于自变量较多，在分析时为了有所侧重，从三个城市中心、公共交通条件（邻近地铁以及公交线路）两个角度来考察城市中心以及通勤情况（成本）对住宅价格的影响，即西湖距离、武林距离、钱江距离、邻近地铁和公交线路五个住宅特征隐含价格的分布情况及其原因。选择这两个角度分析主要有以下两方面原因。首先，杭州逐渐形成了西湖、武林广场和钱江新城三个城市中心，它们各自对周边住宅价格存在一定程度的作用。然而由于各种原因，如三中心形成的时间、成熟度、区位等，可能使得三中心对住宅价格的影响与纯粹的单中心的影响模式的叠加不同。因此，考察三中心对杭州住宅价格的影响，分析它们的隐含价格的空间分布较为必要，这也是本研究关注的重点。此外，随着生活节奏的加快，通勤成本越来越成为购房者选房时考虑的重要因素。但是，私家车的快速增多是否会减弱人们对公共交通的依赖程度，公共交通对住宅价格的影响是如何分布的，也成为人们关注的问题。

①三中心隐含价格分析

从表6.5可知，针对西湖距离这个区位特征而言，在所有样本点中，有79.4%达到10%显著性水平，74.6%达到5%显著性水平，由此可见西湖距离对杭州住宅小区价格的影响较为广泛。虽然它对绝大多数空间位置上的住宅价格都有显著的影响，但是它对不同空间位置的住宅价格有着明显不同的影响。

图6.1直观地揭示了西湖距离对住宅价格影响的显著性情况和空间分布情况（图中A代表西湖）。由图6.1（a）可知，几乎所有样本点达到了1%显著性水平，由此可见，到西湖的距离对住宅价格存在较为明显的影响。从图6.1（b）中可以看出，由西湖往东，西湖距离的回归系数的绝对值总体上呈现逐渐增大的趋势，这说明到西湖的距离直接影响着西湖东面小区的住宅价格，越靠近西湖，价格梯度越缓。购房者在购买该区域住房时，较为看重西湖作为名胜风景区的价值，愿意为更靠近西湖的住宅承受更高的价格，随着离西湖距离的增加，住宅价格下降缓慢，西湖对住宅小区价格的提升较大。而住宅小区的位置越往东，价格梯度逐渐增大，住宅价格下降较快，西湖对住宅小区的影响则逐渐减缓。同样，由西湖不断往东南以及往西北面延伸，西湖对住宅小区价格的影响也是显著递减的。此外，西湖北面和东南面回归系数的绝对值总体上要大于东面的，说明西湖对其北面及南面的住宅价格的影响比对东面的更大。造成这种现象原因可能是，城北以及滨江区的住宅价格相对其他地区较低，西湖距离的住宅价格梯度下降较快，而西湖东面是杭州的老城区，由于其优越的地理位置以及完善的配套设施，该区域的住宅价格一直比较坚挺，其价格弹性反而比西湖北面和东南面更小。

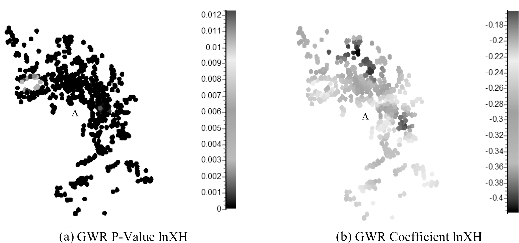
图6.1　西湖距离回归系数P值及回归系数分布

武林广场（图6.2（b）中的B）是杭州传统的商业中心，周边有杭州大厦、杭州百货大楼、杭州剧院等，同时武林广场与杭州市政府和浙江省政府均只有咫尺之遥，最近几年西湖文化广场稳步开发运营，这使得武林广场成为杭州政治、经济和文化中心。从理论上来说，武林广场对其周边的住宅应该存在溢价效应。从图6.2（a）可知，武林广场距离回归系数的显著性随着空间位置的不同有着明显的差异。由表6.5可知，43%的样本点的住宅价格与到武林广场的距离之间存在显著的关系，由此可见，只有不到一半的样本点受到武林广场的影响，不显著的样本点主要分布在武林广场东西两侧较近的区域，这可能是由于这两侧小区与西湖的距离较近，西湖对它们的作用大于武林广场的影响。图6.2（b）给出了武林广场回归系数的分布图，从图中可见，除了武林广场北面的样本点回归系数大于零以外，其他区域的系数均小于零。由此可见，武林广场对北面的样本点几乎不存在影响，这可能是因为城北运河的存在以及城北新的商业中心（如北城天地、运河广场、城西银泰）的建成弱化了武林广场对此区域住宅小区价格的影响。

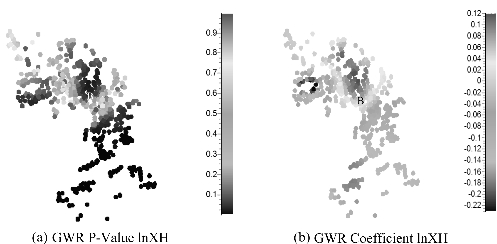
图6.2　武林广场距离P值及回归系数分布

由钱江新城距离的P值图（见图6.3（a））可见，钱江新城（图6.3（b）中的C）对杭州住宅小区的影响主要集中于杭州的东南部，对北部及西北部的样本点几乎没有影响。这是由于钱江新城地处杭州城市的东南边缘，因而其对住宅价格的影响主要存在于城市的东南区域。结合图6.3（b），可以看出东南区域样本点的回归系数大部分都为负值，对于这些样本点来说，随着它们到钱江新城距离的增加，住宅价格有着较为显著的下降趋势，钱江新城对这些样本点的住宅价格有着显著的正向效应。此外，由钱江新城往北，回归系数的绝对值逐渐减小，这说明住宅小区的价格下降得较为缓慢，这主要是由于钱江新城往北分布着庆春路、延安路、解放路等诸多的商业中心街，从而对房价有着显著的正向效应。再不断往北，回归系数逐渐变为正值，且显著性水平也达不到10%。可见，再往北的住宅小区几乎不受钱江新城的影响。主要原因可能有两方面：不断往北的住宅小区与钱江新城的距离不断增加，其影响力势必减弱；从方位上来说，西湖以及武林广场均在钱江新城的西北面，西湖以及武林广场的存在使得该区域的购房者更多地考虑到西湖以及武林广场的距离，这也会弱化钱江新城对住宅价格的影响。从总体上来说，钱江新城对杭州小区住宅价格的影响呈现较为明显的区域性，其影响主要分布在钱塘江的两岸、杭州城市的东南区域。这同时也表明到钱江新城的距离的隐含价格存在显著的空间异质性，前面传统特征价格模型得到的回归系数为-0.059，并且是显著的，若仅仅以此为据来分析钱江新城对杭州住宅价格的影响，则与事实有所不符。

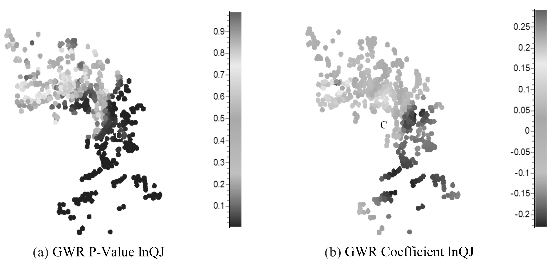
图6.3　钱江新城距离P值图及回归系数分布(www.daowen.com)

②公交线路以及邻近地铁住宅特征分析

特征价格模型结果显示公交线路的隐含价格为-0.002，为负值，但是其绝对值较小。这个结果说明，购房者对杭州住宅小区周边的公交线路考虑得较少，公交线路甚至还存在较小程度上的负面影响。

而GWR模型提供了更为详尽的结果（见图6.4），大部分地区的回归系数都为负值，只有位于城市东北向的部分区域的回归系数为正值。从总体上来说，公交线路对住宅价格存在负面的影响，公交线路带来的负面效应比正面效应更大。而且，从数值上来看，回归系数的正负值均较小。

这一方面可能是因为随着人民生活水平的提高，私家车得到了广泛的普及，人们在购房时对住宅小区周边公共交通的依赖不是很明显，而更加看重其他住宅特征的影响；另一方面，人口数量的分布不均也使得不同地区对公交线路的依赖程度不尽相同并存在一定的差异。此外，地铁1号线的通车以及地铁2号线的预期在一定程度上也对此有所影响，1号线由萧山至下沙，2号线由萧山到丰潭路，两条线路分别由南向北再往东、由南向北再往西，覆盖了大部分的城市中心区域，这也在一定程度上降低了人们对公交车的依赖程度。

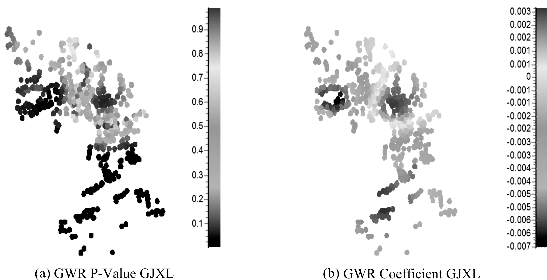
图6.4　公交线路P值及回归系数分布

为了进一步研究是否是人民生活水平的提高以及人口数量分布的不均衡造成了公交线路的隐含价格在空间上的差异，本研究以公交线路的隐含价格为被解释变量，以人均GDP指数和人口密度指数两个变量为解释变量，构建如下模型：

βi=η0+η1X1+η2X2+εi　(6.4)

式中，βi为小区i公交线路的隐含价格，η0为常数项，η1为人均GDP指数X1的回归系数，η2为人口密度指数X2的回归系数，εi为随机误差项。

从各区的统计局网站上收集到六个城区的人均GDP和人口密度的数据，并进行标准化处理，具体过程分别表示为：

公式中的人均GDPj和人口密度j（j=1，2，…，6）分别是六个城区的人均GDP和人口密度。上述线性回归模型的结果如表6.6所示。

表6.6　模型回归结果

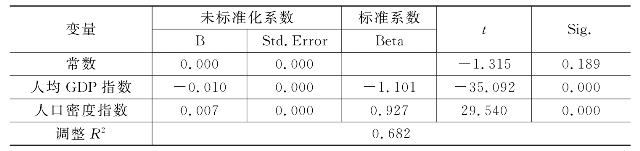
由表6.6可知，人均GDP指数和人口密度指数均达到1%显著性水平，人均GDP指数的回归系数为-0.01，小于零。由此可见，人均GDP指数与公交线路呈显著的负相关。随着人均GDP水平的提高，人们对公交线路的依赖程度下降，公交线路密集甚至可能出现负面的影响，这与之前的推测相符。人口密度指数的回归系数为0.007。由此可见，人口密度指数与公交线路呈显著的正相关，这表明在人口相对密集的城区，公共交通的正面效应较为显著，这也与之前的猜测一致。因此，公交线路的隐含价格与各区域人均GDP的水平以及人口密度的情况紧密相关，随着人们整体收入水平的提高，公共交通的作用会逐渐弱化。而人口越为密集的区域，相对来说对公共交通的依赖也更大。

理论上来说，小区周边若有地铁站，地铁站能够为小区居民的生活和工作带来极大的便利。因此，邻近地铁对小区住宅价格应该存在较为明显的增值作用。然而，这一点在线性回归模型中未得到证实。GWR模型回归表明只有32%的样本点邻近地铁的回归系数达到5%显著性水平，可见受地铁影响的住宅小区只占所有样本的三成左右，这可能是导致前面线性回归模型结果中邻近地铁并不显著的原因。而从GWR模型得到的结果来看，虽然地铁1号线和2号线对周边住宅小区存在一定的影响，但是并不是对所有住宅小区都存在正向的影响，存在正向影响的小区主要存在于西湖以北的西湖区以及拱墅区的部分小区，而位于西湖东面以及东南面的住宅小区的回归系数大都为负值，可见地铁对这部分区域的住宅小区无显著影响。这可能是由于西湖区以及拱墅区新开发的楼盘较多，但是这两个区的公共交通条件与主城区相比相对差一些，居民对地铁的期望更大，而主城区的公共交通原本就较为发达，因此主城区居民对地铁的依赖程度不高。

与前面的公交线路一样，依旧从人均GDP的水平以及人口密度两方面来分析邻近地铁溢价效应的空间异质性。以邻近地铁的隐含价格为因变量，以六城区的人均GDP指数以及人口密度指数为自变量，回归结果如表6.7所示。

表6.7　模型回归结果

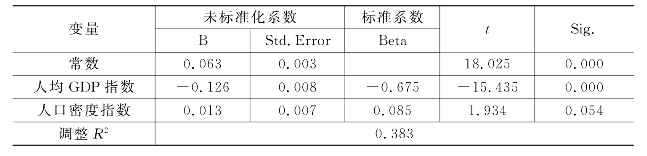
由表6.7可知，人均GDP指数和人口密度指数均达到10%显著性水平，这说明地铁的溢价水平与人均GDP指数及人口密度指数存在显著的线性关系。人均GDP指数的回归系数为-0.126个单位，表明人均GDP指数每提高一个单位，地铁的溢价水平下降0.126个单位；人口密度指数的回归系数为0.013，表明人口密度指数每提高一个单位，邻近地铁的溢价水平上升0.013个单位。因此，人均GDP的水平和人口密度对邻近地铁溢价的空间异质性存在较为显著的影响，在人口较为密集且人均GDP水平相对较低的区域，都可能导致地铁溢价的上升。而人均GDP较高的区域往往交通较为便利（如上城区），这些区域的居民对地铁的依赖程度则较低。