传统的特征价格模型，本质上是回归模型，一般采用最小二乘法（OLS）进行模型估计。由于我们把特征价格模型作为实证分析的基本模型，此处有必要对这些模型进行较为严格的检验，这说明这些模型的结果一方面可被用来分析和比较，另一方面也可间接反映数据的可行性，这些都对后续的实证研究有重要的意义（张之礼，2012；杨尚，2013；陶云龙，2015）。

（1）方差分析

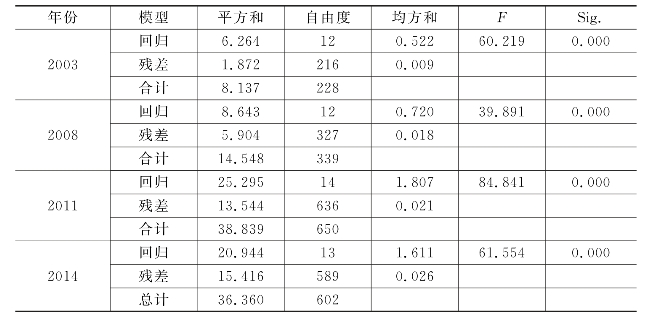
从表5.7可以看出，回归方程方差分析的显著性检验值为0.000（小于0.001），表明回归方程是显著的，从而拒绝了全部系数均为0的原假设。这说明进入回归方程的各解释变量与被解释变量之间的线性关系成立，模型对收集的样本数据的拟合是有统计意义的，所构建的回归方程同样具有意义。

表5.7　方差分析

（2）共线性诊断

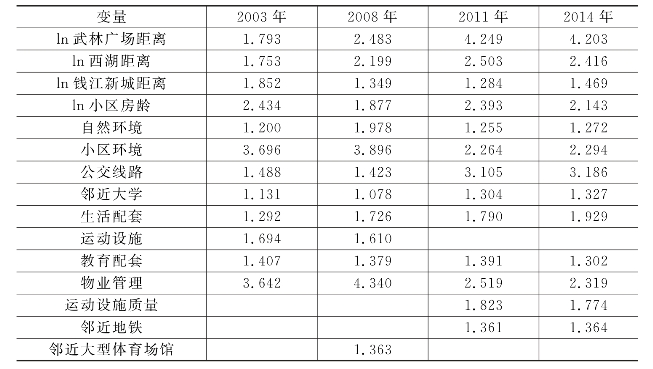
对自变量之间的多重共线性，通常采用方差膨胀因子（VIF）来评价。从表5.8可以看出，各变量的VIF值均小于10，最小值为1.131（2003年），最大值为4.340（2008年），从而可以拒绝自变量之间的共线性假设。可以认为，自变量之间不存在较为严重的共线性问题（温海珍，2004；张之礼，2012）。

表5.8　共线性指标（VIF）分析

（3）异方差检验

从图5.1～5.4可以看出，四个模型的标准化残差绝大部分随机落在-2和2之间，基本满足方差齐性的假设。这表明这些回归模型中不存在严重的异方差问题。

(www.daowen.com)

图5.1　因变量预测值与残差的散点分布（2003年）

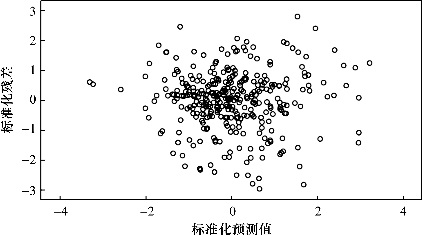
图5.2　因变量预测值与残差的散点分布（2008年）

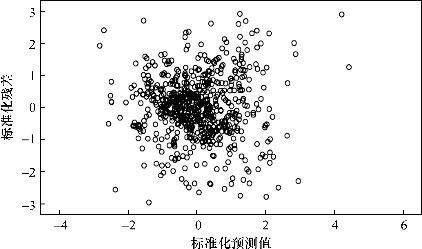
图5.3　因变量预测值与残差的散点分布（2011年）

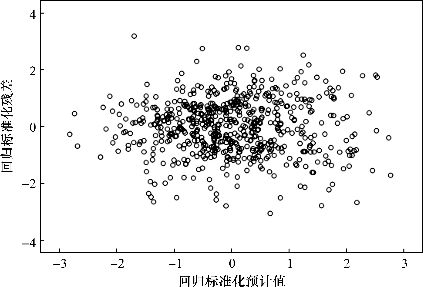
图5.4　因变量预测值与残差的散点分布（2011年）

（4）D-W检验

四个基本模型的D-W值均小于2（见表5.9），说明相邻两点的残差为正相关。由于模型的D-W值均接近于2，因此，可以认为模型各自的误差项基本上是独立的，满足回归模型的前提假设。

表5.9　对数模型的D-W值

总体上，这些检验说明特征价格模型是有效的，可以用来作为分析和比较的基本模型。