借鉴和延续温海珍（2004）、彭鲁凤（2010）、张之礼（2012）和陶云龙（2015）对杭州住宅市场的特征价格分析框架，在实证模型构建时做如下处理。

（1）样本数据的预处理

为了排除样本数据集中奇异值对模型结果的干扰，先对收集到的样本数据进行预处理。用SPSS软件对奇异值进行筛选，默认将标准化残差绝对值大于3的观测值视为奇异值（温海珍，2004）。找出奇异值后，在模型实证前将它们从样本集中剔除，最后得到四个年度的有效小区样本数分别为229、340、651和603个。

（2）变量的选择

在变量设置方面，部分变量相互关联或者从不同方面刻画同一个指标，比如治安环境和物业管理、运动设施质量和运动设施数量，因此，这些变量之间存在较强的共线性问题（温海珍，2004；张之礼，2012）。为了尽量减少变量间的共线性程度，增加模型的解释力，有必要对变量进行选择。经过使用同样的样本数据，采用同样的模型不断尝试，我们发现：公交线路和交通条件、物业管理和治安环境、运动设施和运动设施质量，这三组变量的相关性较强。比如，2011年的数据表明，它们的相关系数分别为0.560、0.588、0.850（张之礼，2012）。我们采用建模比较拟合程度的方法进行变量的优选。在其他变量相同的情况下，采用公交线路、物业管理和运动设施质量的模型效果更好。

经过筛选后，得到的自变量和因变量的描述性统计如表5.2～5.5所示，统计指标包括样本数、极小值、极大值、均值和标准差。例如，从表5.5可知，在2014年的603个有效样本中，因变量小区均价在11493～48706元/平方米波动，均值为23446.08元/平方米，与杭州市房价的实际情况基本相符（杨尚，2013；陶云龙，2015）。

表5.2　因变量和自变量的描述性统计（2003年）

表5.3　因变量和自变量的描述性统计（2008年）(www.daowen.com)

表5.4　因变量和自变量的描述性统计（2011年）

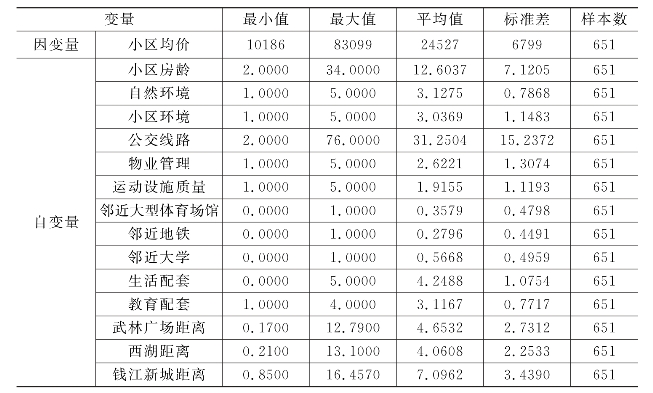
表5.5　因变量和自变量的描述性统计（2014年）

（3）函数形式的选择

特征价格模型的常用函数形式有四种，即线性、对数、对数线性和半对数（温海珍，2004；张之礼，2012；杨尚，2013）。本研究涉及的自变量中，取对数的变量包括武林广场距离、钱江新城距离、西湖距离以及小区房龄。经过尝试，发现对于同样的变量和样本数据，与半对数形式以及线性形式相比，对数函数形式和对数线性函数形式的解释力度明显更高。再结合自变量的显著性情况，最终选择对数函数形式进行模型的拟合。四种函数形式的拟合优度如表5.6所示。

表5.6　四种函数形式的拟合优度