在采用普通回归模型进行分析时,数据取自于地理单元,然后估计单独的回归方程,从而使得所得到的估计的参数具有“全局性”和“平均性”,即假设参数在整个地理空间上是相等的,则认为所测度的空间关系在空间上是平稳的。然而,现实并非如此,在不同的空间区位,被解释变量和解释变量间的关系会发生空间上的变化,往往表现为空间非平稳性,这会给回归模型估计得到的参数的解释带来困难(魏传华,2003)。造成空间非平稳性一个较大的原因是:随着地域的不同,其本身内在的一些关系也会变化,如在不同的地域,政府的管理、治安的环境以及其他一些因素必然不同,人们会根据自己的偏好做不同的选择,这就导致了空间异质性的存在。
Fortheringham等(1996)基于局部回归和变参数的研究,创造性地构建了地理加权回归(geographically weighted regression,GWR)模型,它将回归得到的参数视为空间位置的函数,然后通过局部加权最小二乘方法进行估计,而估计利用到的权重则是对应回归样本所在的空间点到其他所有样本空间点间的距离函数(覃文忠等,2007)。这是地理加权回归模型的优点,它通过这样的函数构造,使得通过回归能够得到不同空间位置上的参数,从而能够更好地反映空间非平稳性。
Tobler地理学第一定律提出地球上的任何事物与其距离近的事物的关系比距离远的事物的关系更大。在此基础上,Fortheringham等提出地理加权回归模型允许局部参数的估计而不是对全局参数的估计。某一位置的回归参数不是所有空间上的任意参数,而是使用其邻近数据的观测值来进行局部回归的估计。地理加权回归模型函数形式具体如下:
式中,yi代表因变量,Xij代表地点i的第j个自变量,βj(ui,vi)代表自变量的回归系数,ui、vi是样本i的地理区位坐标,εi为随机误差项。
地理加权回归模型通过在线性回归模型中假定回归系数是观测点地理位置的函数,将数据的空间特性纳入模型中,为分析回归关系的空间特征创造了条件(玄海燕等,2008)。与传统特征价格模型不同,在地理加权回归模型中,βi随着区位的变化而变化,而不再是固定的回归系数。在用地理加权回归模型进行实证估计时,需要引入权重矩阵,空间权函数的确定方法有距离阈值法、距离反比法、高斯函数法、bi-square函数法等。
如何确定合适的距离阈值D是距离阈值法的关键。将两个样本点之间的距离dij与其比较,若大于该阈值则权重为0,否则为1,即
高斯函数法的公式表达如下:
bi-square函数的公式表达如下:
高斯函数法和bi-square函数中的b是带宽,dij为样本点i与j之间的距离。
模型采用加权最小二乘的方法来估计回归系数。即对于给定的一个地理位置,估计该点处的参数时,对距离该点较近的观测赋予较大的权,对距离该点较远的观测赋予较小的权,通过使观测值与拟合值的加权和(加权误差平方和)达到最小而得到该点参数的估计(覃文忠,2007;玄海燕等,2008)。
可求得在(ui,vi)处参数估计的矩阵表达式:
β(ui,vi)=[XTW(ui,vi)X]-1XTW(ui,vi)Y (2.18)
设(u0,v0)为所研究的地理区域内任一点,在该点处指定一组权:
w1(u0,v0),w2(u0,v0),w3(u0,v0),…,wn(u0,v0)
选择在该点的回归系数:
β0(u0,v0),β1(u0,v0),β2(u0,v0),…,βp(u0,v0)
使得![]() 达到最小,记
达到最小,记![]() 对βj(u0,v0)(j=0,1,…,p)求偏导数,并令其为零,解得β0(u0,v0),β1(u0,v0),…,βp(u0,v0)的估计值为
对βj(u0,v0)(j=0,1,…,p)求偏导数,并令其为零,解得β0(u0,v0),β1(u0,v0),…,βp(u0,v0)的估计值为
令
从而可求得在(u0,v0)处的参数估计的矩阵表达式:
因变量y在(u0,v0)处的拟合值为
式中,![]() =(1,x01,…,x0p)为自变量在(u0,v0)处的取值。
=(1,x01,…,x0p)为自变量在(u0,v0)处的取值。
判断标准(曾晖,2012):与普通最小二乘法相比,R2和经调整的R2是否有所提高;应用AIC准则检验模型拟合优度的标准是:如果两个模型的AIC值相差小于3,则可认为两种模型的拟合优度没有不同。否则,即使考虑了复杂性,也应选择AIC值小的模型。(www.daowen.com)
在地理加权回归模型的基础上所提出的混合地理加权回归(mixed geographically weighted regression,MGWR)模型则是对地理加权回归模型的完善与优化。它是自变量中包含全局变量和局部变量时的一种回归模型,与一般的线性回归模型和单纯的地理加权回归模型相比,可以更加准确地展现空间数据的非平稳性,同时也能更好地解释自变量的系数受空间变化的影响。由于在研究中有些自变量影响因变量可能是全局性的,而另一些则是局部性的,而在混合地理加权回归模型中,有些系数是固定的,但另一些则是变化的,因此,对变量进行这样的设置,更加符合实际情况。混合地理加权回归模型的具体函数形式如下:
式中,yi代表小区i住宅价格的对数,Xij代表地点i的第j个自变量(住宅特征),βj(ui,vi)代表自变量的回归系数,ui、vi是样本i的地理区位坐标。βj(j=0,1,…,q)是未知的常数,对应着模型中的全局变量。βj(ui,vi)(j=q+1,q+2,…,p)代表第i个样本点的未知参数,对应着模型中的局部变量,是(ui,vi)的任意函数。
实际上,混合地理加权回归模型由一个地理加权回归模型和一个线性回归模型组合而成。假定已从X中依次筛选出常系数列,分别为第k0,k1,…,kq列,将这些常系数列以之前的位置排列组成一个新的矩阵Xc,而其余的列按原来的位置不动构成一个新的矩阵Xv,具体表示如下:
并且假设其余的变量表示如下:
βc=[β0β1…βq]T
βv(ui,vi)=[βq+1βq+2…βp]T
进一步假设![]() 为Xv的第i行,并且
为Xv的第i行,并且
W(ui,vi)=diag[w1(ui,vi)w2(ui,vi)…wn(ui,vi)]
是一个n×n的对角矩阵,它的元素一般是取高斯函数的形式:
wj(ui,vi)=exp[-(dij/b)2/2]
式中,b为光滑参数,它是非参数的形式,dij是从(ui,vi)到(uj,vj)的距离。
当前混合地理加权回归的估计方法主要是两步估计法(玄海燕等,2007)。
先将![]() 中的
中的![]() 移项到等式左边,得到
移项到等式左边,得到
根据之前地理加权回归模型的估计演算过程,可以得到在(ui,vi)处的参数估计的矩阵表达式:
式中,S=[XTW(ui,vi)X]-1XTW(ui,vi)称为帽子矩阵,从而获得变系数部分在位置(ui,vi)的估计值:
把变系数部分的估计值代入混合地理加权回归模型的方程中,可以得到
整理方程后得到
(I-S)Y=(I-S)Xcβc+ε (2.27)
令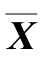 =(I-S)Xc,
=(I-S)Xc,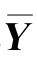 =(I-S)Y,则式(2.27)可改写为:
=(I-S)Y,则式(2.27)可改写为:
此时方程为典型的线性回归模型形式,因而可以使用OLS方法对常参数部分进行拟合估计:
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







