Armstrong（2004）建立了较为完整的双边市场价格分析框架，虽然其研究并不适用于所有双边市场类型，但仍具有一定的适用性基础，对双边市场的定价特征进行了较为完整的概括。本节主要基于其研究成果介绍双边市场分析的基础模型。

▶一、垄断平台基础模型

基本假设：假设平台两边分别为买方B和卖方S，参与数量分别为n B和n S。为简化分析，忽略自网络外部性，只考虑正的交叉网络外部性。参数αB和αS为交叉网络外部性参数，参数αB表示每一个参与平台的卖方用户S给买方用户B带来的外部性，也可将其视为买方B通过平台厂商与卖方S发生每一笔交易所获得的效用，参数αS表示每一个买方用户（B）参与平台给卖方用户（S）带来的外部性，即卖方S通过平台厂商与买方B发生每一笔交易所获得的收益。其中αB＞0，αS＞0。p B和p S分别表示平台向买方和卖方用户提供单位产品或服务的价格。可以得出买方与卖方的效用函数分别为：

u B＝αBn S－p B；u S＝αSn B－p S 　（14.1）

假设平台是通过设定效用｛u B，u S｝，而不是价格｛p B，p S｝来影响需求，则将效用函数转换为：

p B＝αBn S－u B；p S＝αSn B－u S 　（14.2）

为了更准确地刻画平台厂商面临的需求函数，由双边市场的用户通过平台交易获得的效用函数u B和u S可得平台厂商面临的需求，将n B，n S表示为：

n B＝ΦB（u B）；n S＝ΦS（u S） 　（14.3）

成本方面，假设平台厂商为买方B和卖方S提供单位产品或服务的成本分别为f B和f S，则垄断平台厂商的利润函数为：

π＝n B（p B－f B）＋n S（p S－f S） 　（14.4）

将（2）式、（3）式带入（4）式可得：

π（u B，u S）＝ΦB（u B）［αBΦS（u S）－u B－f B］＋ΦS（u S）［αSΦB（u B）－u S－f S］　（14.5）

命题1：社会总福利最大情况下：令买方B的总剩余表示为v B（u B），卖方S的总剩余表示为v S（u S），其中vi满足包络定理v′i（ui）≡Φi（ui）。社会总福利可表示为：w＝π（u B＋u S）＋v B（u B）＋v S（u S）。

由一阶最优条件可得：u B＝（αB＋αS）n S－f B；u S＝（αB＋αS）n B－f S

由式（1）可得社会最优价格为：

p B＝f B－αSn S；p S＝f S－αBn B 　（14.6）

结论1：垄断平台对买方B的最优定价与平台为其提供服务的成本f B以及买方B带给买方S的外部性收益αSn S有关，其中价格的高低与成本大小呈正相关关系，与外部性收益多少呈负相关关系。αS表示每一个买方的参与平台给卖方带来的外部性，因此αSn S表示每增加一个买方B对卖方S所带来的外部性收益。正是因为外部性收益的存在，平台厂商通过转移支付的形式来吸引买方的参与，从而带动卖方的进入。如式（6）所示，这个转移支付的程度等于其所带来的外部性收益。因此，如果买方给卖方带来的外部性收益越大（即αS越大），平台对其定价就越低。特别在αS足够大的情况下， p B可能会低于成本甚至为零，即平台对其进行补贴定价。同理，也适用于卖方一边。

命题2：平台利润最大化条件下：

联合求解得：

联立求解可得到垄断平台利润最大化条件下的价格结构公式：

令εB（n S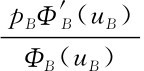）＝表示n S个卖方用户参与平台时，买方用户对垄断平台的需求价格弹性。εS（n B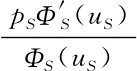）＝表示n B个买方用户参与平台时，卖方用户对垄断平台的需求价格弹性。这时平台利润最大化的价格结构满足：

即产业组织理论中的勒纳指数形式。

结论2：与单边市场进行比较，单边市场上垄断企业利润最大化的价格满足：p＝f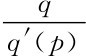＋，与（7）式相比较，可以看出双边市场垄断平台企业对买卖两方的定价中扣除了一方用户给另一方用户带来的外部性即αSn S和αBn B。当网络外部性参数α很大时，平台向用户收取的价格会很低，甚至为零。

单边市场上垄断企业利润最大化下的勒纳指数为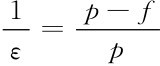：，与（8）式相比较，都是用户的需求价格弹性越大，平台向其收取的价格越低，这一点是一致的。但交叉的网络外部性的存在吸引另一边用户参与到平台，给平台带来了额外的收益，从而降低了平台制定高价的垄断势力。因此，一边为另一边用户带来的外部性越大，即α越大，平台对其制定的价格越低。ε和α的大小差异可表现出平台对两类用户定价的不对称性。如果买方用户的需求价格弹性εB（n）和买方用户参与交易平台给卖方用户带来的外部性参数αS相对越大，那么平台向买方用户收取的价格就越低。

▶二、竞争平台基础模型

引入Hotelling模型描述平台竞争：假设有两个平台进行相互竞争，它们分别位于线性市场［0，1］两端。假设双边用户都是单归属性的，买卖双边用户均匀分布于两个平台之间，且每类用户总和为1单位，即

n1B＋n2B＝1；n1S＋n2S＝1 　（14.9）(www.daowen.com)

平台厂商i＝1，2的双边用户效用可表示为：

uiB＝αBniS－piB；uiS＝αSniB－piS 　（14.10）

t B，t S＞0表示平台的产品或服务对买方和卖方用户的差异化程度参数[6]，同时体现了双边市场的竞争程度。得出：

将式（11）、式（9）带入（10）式中可以得出平台厂商i（i＝1，2）在双边市场的市场份额：

式（12）表示在卖方S承担的价格一定的情况下，平台i每增加一个买方B，将为平台i吸引到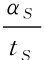个卖方。

假设与差异化参数｛t B，t S｝相比，网络外部性参数｛αS，αS｝很小，均衡存在的充要条件为：

4t Bt S＞（αB＋αS）2 　（14.13）

平台i的利润为：

命题3：结合必要条件（13）对平台利润进行最大值求解，可得：

结论3：单边市场Hotelling竞争模型的均衡价格为：p＝f＋t，与（15）式比较可以看出，交叉网络外部性的存在对竞争平台价格具有负的影响，平台竞争的双边市场均衡价格同样要减去用户间的网络外部效应α。产品或服务的差异化程度t与单边Hotelling模型所阐明的效应一致，平台将对产品或服务差异化程度较小的、外部性较强的一边用户收取低价甚至免费（即不对称的定价）。

命题4：买方和卖方两类用户的对竞争平台的需求价格弹性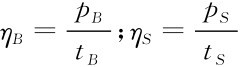：。进一步将（15）式改写为勒纳指数形式：

结论4：比较公式（8）和公式（16）可以发现，竞争平台的勒纳指数对网络外部性效应赋予的权数是垄断平台的两倍。这是由于平台之间的竞争造成的。如果垄断平台提高一边用户的价格，致使边际用户离开市场时，该边际用户将从市场上消失；而在竞争平台中，如果平台i提高一边用户价格，将使其边际用户转换至平台j，用户间的网络外部性会导致平台i的另一边用户也发生相应转换。因此，双边市场中用户间网络外部性的双重效应进一步限制了竞争性交易平台价格加成的能力。

以上基础模型是基于Armstrong（2006）的研究模型总结而得，主要概括了当平台采用注册费方式、两边用户单归属、只存在交叉网络外部性等最简单条件下垄断与竞争平台的行为模型。相较于Rochet和Tirole（2003）所建立的一般模型，此模型考虑了交叉网络外部性的影响机理，建立了更加完整的分析框架，更系统地解释了平台对一边用户亏本甚至免费提供产品和服务的原因。因此现有的文献大多采用此基准模型进行拓展，融入行业特征因素，对双边市场各个不同行业的定价模式和竞争垄断行为等进行研究。

复习思考题

1.双边市场该如何进行界定？

2.双边市场具有哪些基本特征？

3.双边市场具有哪几种常见的分类方式？

4.哪些因素对双边市场价格策略造成影响？

5.双边市场基础模型得出了哪些结论？

[1] 1833年，《纽约时报》在美国掀起“便士报纸”运动，只要一个便士就可以买到一份报纸。因而，普通大众都能买得起，导致该报的销量急剧增加，进而诱发了广告商的吸引力。最终，《纽约时报》不仅销量剧增，而且还获得了大量广告收入。

[2] 1979年，Nabaco公司就对银行卡组织VISA的反垄断妨害提起了诉讼，而经济学家和政策制定者们在对VISA的商业行为进行分析的时候，发现银行卡组织与传统理论中的企业在行为模式和市场绩效方面具有较大的区别，难以用传统理论进行分析。Baxter于1983年发表文章，提出VISA等银行卡组织面对持卡人和商户的联合需求特征，以及不能隔离一个市场考察另一个市场的重要性，这篇文章后来也被认为是最早搭建了双边市场的研究框架。

[3] “鸡生蛋，还是蛋生鸡”这是双边市场基本问题之一。虽然大多模型为了研究方便，假设双边市场的用户是同时进入市场的，但实际上双边市场建立时平台必须选择先吸引哪一边用户进入平台（on board），再利用外部性获取另一边用户。在以某些信息技术为基础的需求协调型双边平台，因其平台所具有的和卖者共同提供产品供给的特性，平台两边用户的进入具有特定的先后次序。比如说，手机应用商城app store必须先引入软件开发商进入以实现软件的供应，再引入消费者进行软件的购买。

[4] 具体影响机理参考第三节模型的构建。

[5] 在竞争性瓶颈均衡中，多平台接入的卖者将获取不到任何交易的剩余，而单平台接入的买者却享受到了一个低于成本的价格。

[6] 通常被称为买卖双方到达平台的单位距离成本。