▶一、豪泰林模型

在研究横向产品差异化的模型中，最常用的方法是区位模型。Hotelling（1929）在《竞争中的稳定性》一文中，开创性提出了产品差异化空间模型方法——豪泰林产品差异化模型，也叫线性城市模型。

在空间差异化模型中，消费者认为每家厂商的产品在地理或产品（特征）空间中均有一个特殊的位置，其中，不同的消费者定位于不同的地方，即消费者具有不同的偏好。两种产品在地理或特征空间中越接近，它们就越是好的替代品。根据产品区别化战略原则，各企业一般都不愿意在产品空间中定位于同一位置。其原因仅仅在于伯特兰悖论：生产完全可替代产品的两家企业，面对无约束的价格竞争。与此相对，产品差别化建立了固定客户，并且允许企业对他们享有某些市场权力。因此，企业通常愿意把自己与其他企业区别开来。下面我们就介绍这个模型，主要关心三个问题：最优定价、最优定位和最优数量。我们这里仅考虑其定价问题。

（一）豪泰林模型基本假定

1.在一个长度为1的线性城市中存在两家商店，他们提供的产品或者服务是同质的；商店分别位于城市的两端，商店1位于x1＝0处，商店2位于x2＝1处，空间上的差异决定了各个商店的产品是差异的；商店1和商店2的边际成本均为c1＝c2＝c，pi为商店i的价格，qi为需求函数，i＝1，2。

2.消费者均匀分布于城市的［0，1］区间内，消费者可以用x∈［0，1］表示；消费者具有单位需求，即消费者只购买1个单位的产品；记每个消费者购买单位产品所支付的交通成本为t，则对于x∈［0，1］上任意一点x的某个消费者来说，购买商店1产品的交通成本为tx，购买商店2产品的交通成本为t（1－x）。因此，消费者向商店1购买的总成本为p1＋tx，向商店2购买的总成本为p2＋t（1－x）。

图3.3 豪泰林（Hotelling）模型示意图

（二）豪泰林模型推导

现考虑两家商店之间的定价竞争。假定两个商店同时选择自己的销售价格，如果住在x的消费者在两个商店之间购买是无差异的，那么，所有住在x左边的都将在商店1购买，而住在x右边的将在商店2购买。

为得到商店1和商店2的需求函数，考虑向两个商店购买无差异的消费者x（p1， p2），由

x＝（p2－p1＋t）/2t 　（3.39）

解上式得

p1＋tx＝p2＋t（1－x） 　（3.38）

因此，商店1和商店2的需求函数分别为

q1＝（t＋p2－p1）/2t 　（3.40）

q2＝1－q1＝（t＋p1－p2）/2t 　（3.41）

因此，商店的利润分别为

π1＝（p1－c）q1＝（p1－c）（t＋p2－p1）/2t 　（3.42）

π2＝（p2－c）q2＝（p2－c）（t＋p1－p2）/2t 　（3.43）

由利润最大化一阶条件为0可得

解上述两个一阶条件得最优解为

p＊1＝p＊2＝c＋t 　（3.46）

每个企业的均衡利润为

π1＝π2＝t/2 　（3.47）

不难得到以下结论：豪泰林所分析的产品差异是由消费者所处的地理位置引起的。在一定条件下，当交通成本t越高，产品对于消费者来说差异性越大，厂商对市场就越有操纵力量，不同厂商出售的产品之间的替代性就会降低，借此厂商就可以制定较高的市场价格，获得高额的垄断利润。

在特殊情况下，当交通成本为零时，商品被认为是无差异的。所以，任何一家商店的产品均有完全可替代性，两个商店也不可能将价格定在成本之上，最优价格等于成本，商店的最优利润为零。

▶二、塞洛浦圆周模型

上面关于线性城市的研究中，探讨了差异化产品的价格竞争问题。由于线性城市存在两个端点，从而有可能导致企业利润函数不连续，进而导致均衡不存在。塞洛普（Salop）在1979年提出了圆周模型，该模型是对豪泰林区位模型的扩展。该模型考察一个圆形的城市，假设消费者均匀分布于该圆周上，由于圆形城市是一个封闭的体系，没有特定的起点和终点，那么就可以克服线性城市模型的缺陷，从而保证了均衡的存在性。圆形城市研究的是，除了固定成本或者进入成本以外没有其他“进入壁垒”情况下的进入和定位问题，主要论证了企业数目是内生给定的。

（一）塞洛普圆周模型的基本假设

1.假设N家企业均匀分布于周长为1的圆周上，每个企业生产一种品牌的产品；每个企业面临的成本函数为Ci（qi）＝F＋cqi（i＝1，2，…，N），其中F为固定成本，c为边际成本，q为产量；利润函数为πi（qi）＝（pi－c）qi－F，其中p代表产品价格。

2.消费者均匀分布在周长为1的圆周上，每个消费者只购买1单位的产品；消费者的单位距离的交通成本为t。消费者的目标是最小化购买价格与交通成本之和。

图3.4 Salop模型示意图(www.daowen.com)

（二）塞洛普圆周模型均衡推导

考虑一个两阶段博弈：在第一阶段，潜在的进入者同时选择是否进入，这些企业并不选择他们的地址，而是一个自动等距离地坐落于圆上。这样最大的差异化就是外生地给定了。在第二阶段，在地址给定的情况下，诸多企业在价格上进行竞争。

为了研究方便，我们将圆形城市的局部拉直成一条直线，我们分析其中一个企业k，企业k只有两个真正的竞争对手：一个是位于其左侧的k－1，另一个是位于其右侧的k＋1。

图3.5 塞洛普（Salop）模型局部示意图

由于企业是对称的，我们假定企业k－1和k＋1制定的价格为pk＋1＝pk－1＝p，那么，到企业k和到企业k－1或企业k＋1购买无差异的消费者距离企业k应满足：（3.48）pk＋tx＝p＋t（1/N－x）

则企业面对的需求函数为

qk（pk，p）＝2x＝（p－pk）/t＋1/N 　（3.49）

因而，企业k的利润函数为

利润最大化的一阶条件为

由于pk＋1＝pk－1＝p，所以，对称的塞洛普纳什均衡为

psk＝ps＝c＋t/N；qsk＝qs＝1/N（k＝1，2，…，N） 　（3.52）

由上式可知，均衡价格是商店数目的递减函数。这是显然的，市场中企业越多，相互之间的竞争越激烈，从而价格越低。如果市场进入是自由的，正利润必然吸引新的进入者，最终每家企业只能获得零利润。零利润条件决定了市场中的企业数目。根据对称性，均衡使得每家企业的需求为1/N。为分析自由进入条件下均衡的企业数量，由自由进入均衡的零利润条件，即

得到

由上式，可得到以下基本结论：

1.Nf＝，企业数目同单位交通成本成正向关系，同固定成本成反向关系。单位交通成本越高，消费者越不愿意到离自己比较远的地方购买产品，每家企业的覆盖率就很小，这将诱使新企业进入。固定成本越高，市场进入成本越高，从而限制了企业数目。反过来说，在高固定成本下，企业数目越多，每家企业的需求就越小，但竞争更加激烈，均衡价格越低，从而进入利润将无法弥补固定成本。

2.pf＝c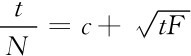＋，企业实行单位成本加成定价，加成幅度随交通成本和固定成本的增加而增大。显然，交通成本越大，固定成本越大，企业数目减少。这将导致企业的市场力量增强。

3.qf＝，产量等于企业数目的倒数。消费者均匀地分布于单位圆周上，具有单位需求，故总需求为1；因为有N家对称的企业，故每家企业得到的市场份额。

现在进行简单的福利分析。社会计划着所关心的问题是：这个均衡与社会最优化有关的企业数量是太多还是太少？为此，社会计划着将选择最优的企业数量，使得固定成本和消费者的交通成本最小：

我们可以证明，最优的企业数量为：N＊＝。这个数量是此模型均衡的企业数量的一半。从而圆形城市模型造成了太多的企业或者品牌。

案例：一个系列化问题

1972年，美国联邦贸易委员会（FTC）对美国四家最大的即食早餐麦片（RTE麦片）的生产企业提出诉讼，指控它们违背了数项反垄断法，包括通过品牌多样化进行合谋，以及差异化相似的产品来阻止企业的进入。尽管FTC没能胜诉，这个争论在理论上还是很有意思的。

理查德·司马伦西（Richard Schmalensee）和F·M·谢勒（F.M.Scherer）使用本地竞争模型解释了FTC的论点。在该模型中，消费者基于麦片的特征进行选择，比如甜度和口感。每个品牌都位于特征空间中。给定品牌必须在其所处的产品空间和邻近品牌争夺消费者。如果公司拥有被它自己的其他类似品牌围绕的品牌，那么它自己的品牌之间就会相互竞争。克洛格公司的麦片和“特别K”可能就是非常相近的替代品。

根据这一品牌扩散理论，如果一家企业创造了足够多的外围品牌或者“防御性”品牌，那么其他企业就可能难以争取到足够多的消费者，以在产品空间的该区域内有利可图地建立一个品牌。类似地，数家企业可以密谋在产品空间的一个给定区域共同建立许多品牌（品牌数量超过短期利润最大化所需要的品牌数），从而阻止新企业进入。

无论企业是否进行了合谋，最大的六家企业占据了麦片市场95％的销售额。而且，在1950～1972年期间，六家领导企业在销售中引入的品牌超过80种。

但是，在1970年代早期，“健康”麦片开始畅销。由于在位企业原先没有开拓这一产品空间，因此新企业（包括高露洁、国际多样化食品、佩特和皮尔斯巴里等巨头）能够进入。到1974年年中，这些“天然”麦片占据了10％的市场。但是很明显，这些前期进入的新企业没能阻止在位企业进入这一产品空间区域。随着在位企业的进入，以及1974年需求高峰过后这一细分市场的需求下降，到1977年后期，除了一家新公司（佩特）外，所有其他新企业都从这一产品空间区域中驱逐出去了。

资料来源：Schmalensee（1978），Scherer（1979）等。转引自《现代产业组织》（第四版）中文版第219—220页。

复习思考题

1.假设某一市场存在两家厂商，生产同质产品，且生产成本为c；假设市场需求函数为p＝a－b Q。试求古诺均衡情况下的两家厂商各自的产量水平以及利润水平，并求出市场均衡价格。

2.假设条件与题1相同，但是厂商1先行动，厂商2后行动。试求古诺均衡情况下的两家厂商各自的产量水平以及利润水平，并求出市场均衡价格。并与题1结果做比较分析。

3.假设条件与题1相同，但是两家厂商合谋形成卡特尔。试求卡特尔均衡情况下的两家厂商各自的产量水平以及利润水平，并求出市场均衡价格。并与题1结果做比较分析。

4.在什么情况下适用Hotelling模型？是产品存在差异化，还是厂商地址的空间距离？为什么？