▶一、古诺竞争模型

非合作寡头垄断理论始于安托万·奥古斯丁·古诺（Antoine Augustin Cournot） 1838年在法国出版的《关于财富理论的数学原理的研究》一书。在该书中，古诺曾提出一种寡头垄断分析方法。今天，我们把这种方法看作是与寻找企业将产量水平作为策略的博弈中的纳什均衡相同的。1821年，古诺以一篇关于机械与天文的重要论文，获得理学博士学位。古诺的论著超出了经济学的范畴，延伸到数学、科学哲学和历史哲学。古诺对现代数理经济学的创立做出了重要贡献。就垄断而言，常见的边际收益等于边际成本的条件，直接来自于古诺的工作（Shubik，1987）。

（一）古诺双寡头

1.模型基本假设。古诺模型的基本假设包括：

（1）市场中只有两家厂商，其他厂商不能进入。

（2）两家厂商生产的产品同质，且生产成本为零，不考虑固定成本。

（3）两家厂商同时进行产量竞争，且在市场上只存续一期。

（4）市场需求函数已知，且为线性需求曲线。

2.模型均衡的推导。设厂商1、厂商2的利润为π1、π2，产量为q1、q2，市场需求函数为p＝a－b Q（a＞0，b＞0），其中Q为市场需求总量，且Q＝q1＋q2。

那么厂商1的利润函数为：

π1＝pq1＝［a－b（q1＋q2）］q1 　（3.1）

在q2给定的情况下，对π1求极值的一阶条件为：

从而可以得到厂商1的最优产量：

上式意味着给定厂商2的产出水平，厂商1就能确定最优的产量水平。我们可以将厂商1的利润最大化产量与厂商2的产量之间的关系总结为一个方程：

q1＝R1（q2） 　（3.4）

这叫做最优反应函数（或反应函数），反映了当一个企业给定它关于对手行动的信念时企业的最优（利润最大化）行动（产量）。

同理，我们也可以推导出厂商2的最优反应函数：

即，对于厂商1的每一个产量q1，厂商2都会做出最优反应，确定能够实现自身利润最大化的产量q2。

联立式（3.3）和式（3.5），我们可得古诺均衡解：

正如图3.1中表示，两家企业的最优反应曲线相交于点E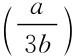，而这点正是两家企业实现各自利润最大化的点。

图3.1 古诺竞争中厂商的最佳反应曲线

在古诺均衡时，两家厂商的产量都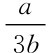为，总产量为，均衡价格为，两家厂商的利润为。

（二）N家厂商的古诺均衡

1.模型推导。现在假设市场中有N家同质厂商，N≥1，其他基本假设同前。那么厂商i的利润函数为：

一阶条件为：

因此，企业i的最优反应函数由下式给出：

由于所有厂商同质，那么在均衡情况下，所有厂商的产量水平都相同，假设每个厂商的均衡产量为qc，代入上述反应函数，可得：

均衡价格与每家厂商的利润水平分别为：

2.进一步分析。我们进一步考虑，当改变市场中厂商数量时，古诺价格、产量和利润水平将如何变化。第一，当N＝1时，可得到完全垄断情况下的解。第二，当N＝2时，可得到古诺双寡头竞争的解。

当厂商数量无限大，即N＝∞时，我们可得：

也就是说，在古诺均衡中，当厂商数量无限大时，每家厂商的产出水平接近于零，市场中总产出接近于完全竞争市场的产出水平，古诺均衡价格接近于厂商单位产品成本（为零）的竞争价格。

▶二、伯川德模型

伯川德模型是由法国数理经济学家伯川德（J.Bertrand）在1883年对古诺模型进行批评与修正基础上提出的。伯川德认为，寡头市场的厂商之间应该存在激烈的价格竞争，因而古诺模型中假设厂商选择产出作为决策变量是不合适的，应该选择价格作为决策手段。

（一）伯川德模型的基本假设

伯川德模型与古诺模型在前提假设上的唯一区别是：在伯川德模型中厂商的决策变量是价格而不是产量。因此，伯川德模型的基本假设包括：

（1）市场中只有两家厂商，其他厂商不能进入。

（2）两家厂商生产的产品同质，且生产成本为常数。

（3）两家厂商同时进行价格竞争，且在市场上只存续一期。

（4）市场需求函数已知，且为线性需求曲线。

（二）伯川德均衡的推导

设厂商1、厂商2的利润为π1、π2，价格分别为p1、p2，边际成本均为c，市场需求函数为Q＝a－bp（a＞0，b＞0）。那么厂商1的利润函数为：

π1（p1，p2）＝（p－c）·q1（p1，p2） 　（3.14）

其中q1为厂商1所面对的需求函数，这一需求函数可以表示为：

从式（3.15）可知，当厂商1的定价p1低于厂商2的定价p2时，厂商1将获得整个市场份额，得到全部利润；当厂商1的定价p1高于厂商2的定价p2时，厂商1将失去整个市场，相应的利润也就为零；当两家厂商的定价相同时，由于两家厂商生产的产品同质，具有完全的替代性，因此两个厂商将均分市场份额。同理，我们也可以得到厂商2的利润函数π2和需求函数q2。

根据伯川德的基本假设以及我们对厂商利润的上述分析，可以得到伯川德均衡，其最后的解为p＊1＝p＊2＝c，且这一均衡是稳定的。

我们可以通过反证法证明。不妨设均衡解为p＊1＝p＊2＞c。此时，两家厂商平分整个市场需求，都获得正的利润π＊i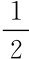＝（p＊i－c）（a－bp＊i）。然而，这个解并不稳定：当厂商1略微将价格降为＝p＊1－ε（ε是一个非常小的量），那么厂商1将获得整个市场并将利润提高到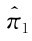＝（p＊1－ε－c）［a－b（p＊i－ε）］，显然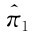＞π＊1。因此，厂商1有激励向下偏离价格。同理，厂商2也有激励降价，并且两家厂商将交互降价，直到p＊1＝p＊2＝c。此时，两家厂商都没有激励降价，并且获得零利润。同理，我们可以证明其他所有情况也不是均衡结果，如p＊1＞p＊2＝c，p＊2＞p＊1＝c，p＊1＞p＊2＞c， p＊2＞p＊1＞c等情况。

（三）伯川德悖论

伯川德均衡的含义在于，如果市场中的两家厂商生产同样的产品，并且成本相同，那么他们之间的价格战必定使得每家厂商都按照p＝MC的原则定价。由此可见，伯川德模型的均衡价格、均衡产量与完全竞争市场中的长期均衡价格、均衡产量完全一样，这显然与实际经验不符，因此伯川德均衡也被称为伯川德悖论（Bertrand Paradox）。

与古诺模型相比，伯川德模型关于厂商选择价格而不是产量作为决策变量的假设似乎更贴近现实。但是，古诺模型关于寡头市场的经济绩效介于完全竞争与垄断之间的结论相对于伯川德均衡的极端结论似乎又更符合直觉。因此，伯川德悖论也被称为古诺—伯川德悖论。

伯川德模型之所以会得到这样的结论，与它的前提假设有关：产出是同质的，市场只存续一个时期，而且任何企业都可以用不变的边际成本生产任意数量的产品。如果放松其中任一假设，伯川德价格就不等于边际成本。在这种情况下，围绕伯川德悖论展开的研究成为此后寡头市场理论发展的一个重要主题。

▶三、斯塔克尔伯格模型

斯塔克尔伯格（Heinrich von Stackelberg）于1932年提出了第三个重要的寡头垄断模型，即斯塔克尔伯格模型，在该模型中，厂商决策变量为产量，并且一个厂商在其他厂商行动之前行动。先行动的厂商为领导厂商。领导厂商选择产量水平，而后其他厂商根据领导厂商的产出水平，决策自己的最优产量水平。

（一）斯塔克尔伯格模型的基本假设

斯塔克尔伯格模型的基本假设主要包括：

（1）市场中只有两家厂商，并且地位不相等，其中厂商1为领导者，厂商2为追随者。

（2）两家厂商生产的产品同质，且生产成本为零。

（3）两家厂商的决策变量为产量。

（4）市场需求函数已知，且为线性需求曲线。

（二）斯塔克尔伯格模型均衡推导

在斯塔克尔伯格模型中，由于两个寡头厂商在市场中所处的地位不同，因而存在着行动次序的区别。产量的决定依据以下顺序：领导厂商首先自行决定获得利润最大化的产量，然后跟随厂商根据领导厂商的产量来决定自己的产出水平。并且由于完美信息，领导厂商在决定自己产量的时候，能够充分了解跟随厂商的行动。也就是说，领导厂商知道跟随厂商的最优反应函数，所以领导厂商决定的产量是一个以跟随厂商的反应函数为约束的利润最大化产量。

我们设厂商1、厂商2的利润为π1、π2，产量为q1、q2，市场需求函数为p＝a－b Q（a＞0，b＞0），其中Q为市场需求总量，且Q＝q1＋q2。假设厂商1为领导厂商，厂商2为跟随厂商。依据逆向归纳法，从动态博弈的最后一步往回推，以求解动态博弈的均衡结果。

也就是说，首先分析厂商2的决策。由于厂商2在决策前已观察到厂商1的产量，所以厂商2将厂商1的产量作为给定的常量。那么，在给定q1的条件下，厂商2的利润函数为：(www.daowen.com)

π2＝pq2＝［a－b（q1＋q2）］q2 　（3.16）

那么，厂商2利润函数的一阶条件为：

上式意味着给定领导厂商的产量，跟随厂商的最优产量反应函数为：

接来下分析博弈的第一阶段，厂商1的目标函数为：

π1＝pq1＝［a－b（q1＋q2）］q1 　（3.19）

将式（3.18）代入式（3.19）中，可得

由利润最大化一阶条件等于零，可得厂商1的最优产量：

将式（3.21）代入式（3.18），可得追随厂商2的最优产量：

相应的，在斯塔科尔伯格均衡下，市场均衡价格为a/4，领导厂商与追随厂商各自获得的利润为a2/8b和a2/16b。作为跟随者，厂商2获得的利润只有领导厂商利润的一半，这说明在斯塔科尔伯格模型中，先动者具有相对优势，而后动者具有相对劣势。

（三）斯塔科尔伯格均衡的绩效分析

表3-1列出了相同市场需求和供给（市场反需求函数为p＝a－bq，生产成本为零）条件下，不同市场类型的均衡产量水平、价格水平以及厂商利润水平。

表3-1

如表3-1所示，处于均衡状态时，与古诺厂商相比，斯塔克尔伯格领导者的产量较高，而跟随厂商的产量较少，斯塔克尔伯格均衡时的总产量比古诺总产量大，但少于完全竞争市场中的产量水平。相应的，斯塔克尔伯格均衡时的价格高于完全竞争市场的均衡价格，但低于古诺竞争中的均衡价格。

▶四、价格领导者模型

斯塔克尔伯格模型中的跟随者是产量跟随，那么，如果先动厂商确定价格，跟随厂商采取跟随价格策略，寡头间的博弈将会产生什么样的结果呢？我们可以用价格领导者模型进行分析。

（一）价格领导者模型的基本思路

假定市场中只存在两家厂商。其中厂商1为领导者，是市场价格的确定者；厂商2为跟随者，是价格的跟随者。当然，由于完美信息，领导厂商1在确定价格水平时，已充分考虑了跟随厂商2的反应。同样的，依据逆向归纳法，我们先分析跟随厂商的行为，再分析领导厂商的先动行为。

假定厂商1确定的价格水平为p，厂商2作为价格的接受者，通过最优化产量水平，获得最大化利润。厂商2的利润函数可用下式表示：（3.23）π2＝pq2－C2（q2）

相应的，利润最大化的一阶条件为：

p＝MC2（q2） 　（3.24）

也就是说，厂商2按照边际收益等于边际成本原则确定自己的最优产量水平，相应的供给函数设定为S2（p）。那么，厂商1面临的剩余市场需求R（p）则为市场总需求D（p）扣除厂商2的供给S2（p），即：（3.25）R（p）＝D（p）－S2（p）

对于厂商1来说，在决定价格p时，必须充分考虑到一旦将价格定为p，自己将面临的剩余需求则为R（p）。在这种情况下，厂商1必须按利润最大化原则首先测算q1，然后确定最优p。

如图3.2所示，D为市场需求曲线，S2（p）为厂商2的供给曲线，假如领导厂商将价格定为p1，市场需求完全由厂商2供给，消费者对厂商1的需求量为零。如果领导厂商将价格定为p2，则市场需求完全由厂商1供给，消费者对厂商2的需求量为零。由此，厂商1面临的剩余需求曲线为d曲线，p1AE［即d＝R（p）＝D（p）－S2（p）］。对于剩余需求来说，厂商1可以像完全垄断者一样行动：依据边际收益等于边际成本确定最优产量与价格水平。

图3.2 价格领导厂商定价策略

（二）价格领导者模型均衡推导

假设市场需求函数为D（P）＝a－p，且两家厂商生产产品成本为C（q）＝。作为价格跟随者的厂商2根据p＝MR2＝MC2原则决定其供给。那么，相应的供给函数为：

S2（p）＝q2＝p 　（3.26）

此时，厂商1面临的剩余需求为：

R（p）＝D（p）－S2（p）＝a－2p 　（3.27）

厂商1的利润函数为：

最大化厂商1利润的一阶条件为：

即，q1＝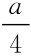

那么，p＝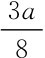

由于S2（p）＝q2＝p，所以q2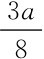＝。也就是说，作为领导者的厂商1将价格确定为p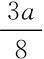＝时，两家寡头厂商的产量分别为q1＝，q2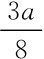＝。这表明，在成本相同的情况下，价格领导者的收益将低于价格跟随者的收益。与产量领导模型相反的是：在成本相同情况下，寡头厂商更愿意选择价格跟随策略而不是价格领导策略。

▶五、卡特尔

前面讨论了寡头企业间的非合作竞争行为，不过，现实中的厂商也常常选择合作行为，以提供高预期收益。其中，卡特尔是合作策略性行为的一种典型形式，它是通过协议（或默契合谋）统一协调行动的厂商之间结成的联盟。

（一）卡特尔合作的模型推导

假设市场中有两家厂商，i＝1，2，各自产量为qi，成本为Ci（qi）＝cqi，市场需求函数为p＝a－bq，决策变量为产量。

1.非合作博弈——古诺博弈。厂商的利润函数为：（3.30）maxπi（q1，q2）＝qip（q1，q2）－ci（qi）

利润最大化的一阶条件为：

将Ci（qi）＝cqi与p＝a－bq代入上式，可得：

2.合谋——卡特尔。此时两家厂商的目标是最大化整个卡特尔组织的利润，即类似于完全垄断企业的行为。那么，卡特尔组织的利润函数为

π＝q（a－bq）－cq 　（3.34）

那么，利润最大化的一阶条件为：

即

比较（3.32）式与（3.37）式，可以看出厂商更愿意合谋而不是竞争。

（二）卡特尔的形成与执行

1.有利于卡特尔形成的因素。

（1）提高市场价格的能力。只有预期卡特尔能够提高价格并将其维持在较高水平的情况下，企业才愿意加入。卡特尔面对的需求曲线弹性越小，它能够制定的价格越高，得到的利润也越大。如果卡特尔的需求曲线是没有弹性的，那么提高价格能够明显地提高收益。相反，如果卡特尔面对高弹性的需求曲线，其提高价格将导致收益下降。

（2）缺乏严厉惩罚。只有当成员预期不会被政府抓到，并受到严厉惩罚时，卡特尔才会成立。较大的惩罚预期能够降低组建卡特尔的预期价值。

（3）较低的组织成本。即使卡特尔在长期来看，能够提高价格且不被发现，如果组织成本过高，卡特尔也难以形成。具体来说，有四方面的因素能够降低组织成本，有利于卡特尔的形成：涉及企业数量少，能够降低政府察觉并进行惩罚的可能性；市场集中度高，能够保证少数几家企业就可以协调卡特尔合谋行为并抬高价格，而不涉及市场中的较小企业；产品同质，能够更易于卡特尔察觉成员企业的欺骗行为；而行业协会，能够降低市场中企业协调成本。

2.卡特尔协议的执行。

（1）市场中企业数量较少。此时，卡特尔能够更容易地对每家企业进行监督。在这种市场环境中，某家企业市场份额的提高就更容易被发现，相应的，发现这家企业背叛（降低价格）行为也更为容易。

（2）价格波动小。如果市场的需求、投入成本以及其他因素频繁发生变动，那么市场产品价格也不得不经常调整。在这种情况下，背叛卡特尔协议的欺骗就很难发现。因为，人们很难区分价格波动的真实原因。

（3）价格信息公开。价格信息的公开获得，能够极大简化卡特尔协议的执行。当所有企业在它们的所有销售中都使用同一个销售代理人或代理组织时，就会出现信息分享的极端情况。

（4）在产业链同一环节销售同质产品。如果某些企业是纵向一体化的，卡特尔就很难确定背叛行为发生在哪个环节。而如果所有企业都把产品销售给同一类型客户，则背叛行为就很容易被发现。

案例：美起诉中国维C企业合谋涨价

占美国维生素C市场80％份额的中国产品，将再次面临反垄断诉讼的压力，据估计最坏的情况是赔偿损失的三倍。

据彭博社报道，纽约布鲁克林联邦法院的一个陪审团将在15日开始商讨。代表原告方美国食品供应公司和维生素C制造商的律师14日在一份民事起诉书中称，中国维生素C制造商违规涨价。美方原告诉讼理由可谓一成不变。美国维生素C反垄断案始于7年前，美国商务部早在2006年就表示对此事“很感兴趣”。美国一些企业控诉中国若干维生素生产商由2001年12月开始共谋控制出口到美国和世界各地的维生素C的价格及数量，触犯了美国反垄断法。但相关中国公司没有真正面对法院审理，因为法院驳回美国维生素C反垄断诉讼原告对公司的全部诉讼请求。法院认定原告对公司行使管辖权缺乏法律依据，故驳回原告起诉的动议。此次法院有可能受理并进行审判。不过美方公司的代理律师赛罗塔称，此次将成为首起中国公司在美国面临的反垄断诉讼。中国制药集团、华北制药公司被列为此次的被告。

此案历时漫长，最初接手该案的地方法官在2011年已经去世。现在负责该案审理的是纽约布鲁克林地方法官柯根。原告方德克萨斯州的“动物科学制品”公司和新泽西的食品公司“拉尼斯”在2005年就提起诉讼，称中国公司通过减少供给量来操纵价格。原告称中国公司操纵价格，令当时维生素C从每千克2.5美元上升至15美元。

来源：经济参考报 日期：2013 03 15