上述ADF单位根检验表明，各变量之间可能存在协整关系，本节采用Engle-Granger两步检验法对其协整性进行检验。

首先进行OLS回归。以5%显著水平为标准，运用Eviews 6.0对公式（2）进行OLS回归，得到以下回归结果：

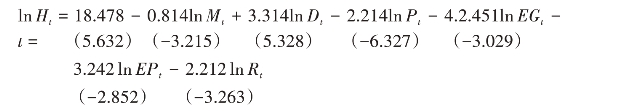
其中，R2=0.822，F=9.327（2.79）DW=1.845

检验结果显示，R2=0.822，说明模型对数据的拟合度达到了R2=0.8的合理边界，其拟合度较为理想。F=9.327，大于其临界值F0.025（6，8）=3.58，表明自变量在总体上能对因变量进行有效解释。DW值在其序列无关范围1.79～2.21之内，表明各自变量具有无自相关性质。||ti＞t0.025（8）=2.306，说明解释变量都在95%的水平下通过变量的显著性检验，其误差处在合理界限范围内。检验结果表明：农村分配结构调整变量的系数为正，表明收入差距扩大会增加农村贫困，从而不利于农村减贫进程推进；除此之外，农村其他各类经济结构调整指标系数为负，表明其调整有力推动了农村贫困减少。(www.daowen.com)

其次是检验残差序列的平稳性。设et是偏离长期均衡关系的离差值，则根据该模型计算残差。本书采用AEG方法对et序列进行检验，其结果如表4-15所示：

表4-15　残差ADF单位根检验结果

由表4-15可知，残差序列et的ADF统计值小于10%和5%显著水平下的临界值，说明残差序列et在95%的水平下是平稳的。

上述Engle-Granger检验表明，公式（2）中自变量和因变量之间存在长期均衡关系，而且这种均衡关系是稳定的。