在经济学中，边际成本是指每单位新生产（或购买）产品引起的总成本增加的部分，这表明产品每个单位的成本与产品的总量有关。例如，生产第1台自助取款机的成本很高，因为从零开始，除了需要一些原材料外，还需要厂房、生产机器等，而生产第1 000台自助取款机的成本要低得多。

我们从数学角度来分析一下边际成本。假设某企业的某产品的产量为m，成本为C=f（m），则第m个产品的成本为f（m）-f（m-1）=Δf（m）≈dC（m）=C′（m），我们称C′（m）为边际成本函数，因此边际成本就可以约等于函数的变化率，它的意义就是在产量为m0的基础上，生产下一个产品，则总成本将增加C′（m0），需要注意的是，这是一个瞬时值。我们通常利用边际成本作为总成本的函数变化率预估边际成本，为企业管理者制订在现有成本基础上的最佳产量提供了依据。

例2：假设某企业的产品总成本C（万元）具有函数关系：C（m）=0.02m3-0.4m2+4m+150，其中m（万件）为产量。

当该产品的产量为10万件时，则该产品的平均成本为

即该产品的产量为10万件时，产品的平均成本为17元/件。此时产品的边际成本为C′（10）=0.06×102-0.8×10+4=2（元/件），从经济意义上来说，在该产品的产量为10万件的基础上，每多生产1件，产品的总成本增加2元，此时产品的边际成本比平均成本要低。若只从考虑降低产品成本的角度看，该企业可以提高产量从而降低成本。

当该产品的产量为20万件时，则该产品的平均成本为

即该产品的产量为20万件时，产品的平均成本为11.5元/件。此时产品的边际成本为C′（20）=0.06×202-0.8×20+4=12（元/件），从经济意义上来说，在该产品的产量为20万件的基础上，每多生产1件，产品的总成本增加12元，此时产品的边际成本比平均成本要高。若只从考虑降低成本的角度看，该企业不能再提高产量，应该降低产量，使该产品的平均成本降低。

从上述例题的计算过程可以看出，当产品的边际成本C′（m0）低于平均成本时，可以在此时产量的基础上提高产品的产量，使得产品的平均成本降低；当产品的边际成本C′（m0）高于平均成本时，可以在此时产量的基础上降低产品的产量，从而降低产品的平均成本；当边际成本C′（m0）等于产品的平均成本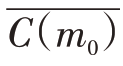时，可以得到此时产品的平均成本最低，此时产品的产量可以作为该企业在现有成本的前提下的最佳产量。

类似边际成本的概念，边际收益是指增加一单位产品的销售所增加的收入，即最后一单位产品的售出所取得的收益。它可能为正值，也可能为负值。

假设某企业某产品的总利润为L（q）（总利润是关于产量q的函数），则我们称L′（q）为商品的边际利润。它的边际利润的经济意义就是在产品的产量为q0的基础上，每多生产一个产品，则该产品的总利润增加L′（q0）。显然只考虑利润的前提下，若L′（q0）＞0时，在产量为q0的基础上，每多生产一个，总利润增加L′（q0），此时可提高产量，使得总利润增加；若L′（q0）＜0时，每多生产一个，总利润减少L′（q0），此时需降低产量，增加总利润；若L′（q0）=0时，每多生产一个，总利润不变，此时可以视为最优化生产状况。

例3：某商店出售某种商品，每件进价55元。若每件销售定价64元，则每天可销售300件，且定价每降低1元，每天可多售出50件该商品。问：每件售价为多少时，能够获取最大利润？此时，进货量为多少？

示例分析：设每天的销售量为x件，售价为p元/件，则两者之间的线性关系是：

化简可得：

x-300=50(64-p)……①(www.daowen.com)

利润L（p）的函数解析式为：

L(p)=x(p-55)=-50p2+6 250p-192 500

=-50(p-62.5)2+2 812.5

所以，当p=62.5时，x=375，L（p）取得最大值L（62.5）=2 812.5（元）。

上面的例题是中学数学中比较常见的利润最大化的应用题，基本思路是用数量乘以每件商品的利润，构造利润L关于价格p的一元二次函数，通过求函数最值，来求解利润的最大值。如果从边际利润的角度理解，则应构造利润L和数量x之间的函数关系式。

利用上述求解过程，容易求得：

因此，每多卖出一个单位的商品所获得的利润，即边际利润为：

令L′（x）=0，求得x=375。

由于此处边际成本不变，进价均为55元。而销售定价降低，才能多卖出商品，边际收益递减。所以，当x＜375时，边际利润L′（x）＞0；当x＞375时，边际利润L′（x）＜0。只有当x=375时，边际利润L′（x）=0，此时，能够获取最大利润。

我们再来分析这道例题的经济学背景。商品的销量随售价的降低而增加，这是由需求定理决定的，具体来讲，由①式便可得到需求函数x=3 500-50p，它的图像是一条线性的需求曲线。有时候，我们还关心需求量随着价格的增长而减少，每上涨1元，需求量下降50件。有时候，我们还关心需求量对价格的敏感程度——需求弹性。

对弹性分析中，设某个经济函数为y=f（x），若f（x）在x处可导，则我们称为在x处的弹性。弹性函数反映了当x改变了1%时，因变量改变了Ex%。

比如，此例中的弹性。因此，这件商品需求弹性函数的经济意义就是，当商品的价格上涨1%时，商品的需求量x将减少Ep%，而当商品的价格下降1%时，商品的需求量x将增加Ep%。在利润最大时，即价格p=62.5时，此时的需求弹性为，即在商品的价格为62.5元的基础上，若商品的价格上涨（下跌）1%时，需求量x将减少（增加）约8.33%。显然Ep＞1，是高弹性的，说明商品的需求变动的百分比高于价格变动的百分比，表明商品价格的变动对需求量的影响较大。