我们常常会遇到生活中的一个问题，到底什么时候去食堂好呢？

假设此时食堂只有2人吃饭，他们的选择均有两种，即早去或者晚去食堂，建立博弈矩阵如表4-4：

表4-4　A、B两人的收益矩阵

（注：表中的数字为收益，规定吃到热饭的收益为+1，无须排队的收益为+1，两个条件都未达到则记收益为0）

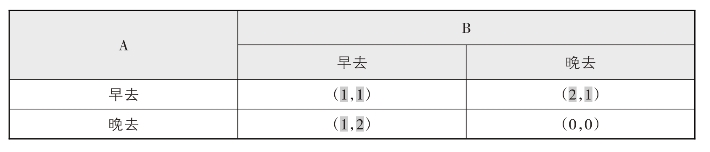
如果A选择早去，此时若B也选择早去，那么A、B两人都能吃到热饭，但是需要排队，所以A、B各自收益为1；若B选择晚去，那么A可以吃到热饭且不用排队，收益为2，但是B吃不到热饭不用排队，收益为1。

如果A选择晚去，此时若B选择早去，那么A吃不到热饭但不用排队，收益为1，B可以吃到热饭且不用排队，收益为2；若B也晚去，则两人都吃不到热饭且都要排队，收益各自记为0。

所以对于A而言，只要B选择早去，A无论是早、晚去都可以获得收益1，得到不错的结果，但是B晚去时，A选择早去可以获得收益为2，晚去就只有0了，所以A可得收益的策略如表4-5标出的部分所示：

表4-5　A的收益策略矩阵

对于B而言，只要A选择早去，B无论是早、晚去都可以获得收益为1，得到不错的结果，但是A晚去时，B选择早去可以获得收益2，晚去就只有0了，所以B可得收益的策略如表4-6标出的部分所示：（其实A、B两人位置等同，表格具有对称性）

表4-6　B的收益策略矩阵(www.daowen.com)

将两张表合并：

表4-7　A、B两人可得收益的策略矩阵

那么表4-7标出的三种策略组合都是纳什均衡。那么问题就变成了这三个纳什均衡均存在，我们的结果会最终达到哪个呢？还是说以某种概率随机分布？早去或晚去的影响又体现在哪里呢？接下来我们采用混合纳什均衡来寻找最后的结果以及我们应该做怎样的决策。

假设B选择早去的概率是P，选择晚去的概率则是1-P，那么对于A来说，选择早去的可能的收益是1P+2（1-P）=2-P，选择晚去的可能的收益是P+0×（1-P）=P，在混合纳什均衡中有个很重要的定理：B的策略选择会使得A选择早去和选择晚去的收益相等，即2-P=P。

如果2-P＞P，即对于A而言，早去的收益比晚去的更大，那么A就直接选择早去，此时就变成纯策略问题，不必使用混合策略的纳什均衡。如果2-P＜P，即对于A而言，晚去的收益比早去的更大，那么A就直接选择晚去，也会回到纯策略问题。所以必须让早去和晚去的收益相同，即2-P=P，就达到了和B同等的有一定概率选择早去和晚去的效果。

此处对于纯策略和混合策略的理解，其实就相当于在两人中选择成绩优秀的人。如果知道其中一人更高，肯定不会选择另一人，只有两人分数一样时才会比较纠结，或者说有概率随机选择某人。

根据2-P=P，可以解得P=1，即B早去的概率为1，晚去的概率为0。在这个前提下，A早去和晚去才产生了概率的随机分布，即无法确定选择早去还是晚去，混合了早去和晚去这两个策略，变成了混合纳什均衡。那么A选择早去的概率和选择晚去的概率具体为多少呢？那就要从B的收益上来考虑。假设A选择早去的概率是Q，选择晚去的概率则是1-Q，那么对于B来说，选择早去的可能的收益是Q+2（1-Q）=2-Q，选择晚去的可能的收益是Q+0×（1-Q）=Q，同理可得2-Q=Q，解得Q=1。可得A的混合策略是P（早去，晚去）=（1，0），B的混合策略是Q（早去，晚去）=（1，0）。

所以，无论从A还是B的角度计算混合纳什均衡，都是早去食堂为最优策略，而且去得越早收益也会越大。这里我们限定为2人博弈，多人博弈的效果是类似的，也就是食堂一开门，第一个冲过去是最好的方案。可以理解为，如果早去食堂，必然能吃到热饭还有可能不用排队，而晚去食堂不仅菜冷了，而且还有可能需要排队，这样描述，更容易判断最优策略的选择。虽然对于生活中的具体情况，早去或者晚去食堂都是具体原因和复杂因素决定的，对于时间的控制，甚至还有想不想吃饭的根本利益变化。我们通过博弈论研究出的最优策略也是仅限于单纯环境下的简单模型，直观解释会更易理解。

通过食堂吃饭问题，我们了解了混合策略中的纳什均衡问题的解决方法，这也是稍微复杂但更具现实意义的博弈模型。