为了下面的分析考虑，我们做一个简单化的假设，假设石师傅短期内无法扩大工厂的规模。比如，他缺少新建厂房和购入新数控豆干机的资金，即工厂规模是固定的，他仍然可以通过增加工人数量来增加豆腐干产量，我们通过这样的假设来分析描述石师傅短期内面临的生产决策。

假设石师傅的工厂中没有工人，就生产不出豆腐干；当有1名工人时，每天可以生产60包豆腐干；当有2名工人时，每天可以生产100包豆腐干；当有3名工人时，每天可以生产130包豆腐干；当有4名工人时，每天可以生产150包豆腐干。那么当工人数量从1人增加到2人时，产量就从60包增加到100包，这增加的40包就叫作第二名工人的边际产量。类似地，第三名工人的边际产量就是30包豆腐干，第4名工人的边际产量是20包豆腐干。而第三名工人的边际产量比第二名工人的边际产量减少了10包豆腐干，第四名工人的边际产量又比第三名工人的边际产量减少了10包豆腐干，这个特征叫作边际产量递减。具体定义如下：

一般地，在保持其他生产要素不变的前提下，增加其中某种生产要素一个单位的投入所引起的产量增加量叫作边际产量。该种投入的边际产量随着投入量的增加而减少的特征叫作边际产量递减。

表3-1的第三列给出了每名工人的边际产量，之所以第二名工人的边际产量40包位于第二行和第三行中间，因为它代表当工人数量从一个水平增加到另一个水平时产量的变动。由于受机器和厂房规模等因素的制约，我们从表3-1中可以看到，豆腐干产量并不会随着工人数量的增加一直增加下去，这也是边际产量会逐步递减的原因。

表3-1　生产函数与总成本（石师傅的豆制品厂）

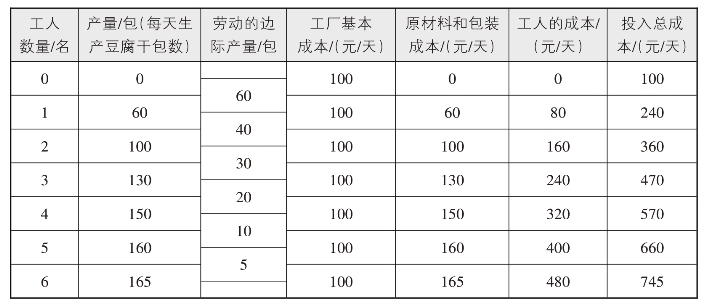
就像表3-1中第一列和第二列所反映的那样，在其他条件不变的情况下，豆腐干产量是关于工人数量的函数，这是企业生产投入量与产量之间的一种函数关系，我们把这种函数关系叫作生产函数。具体定义如下：(www.daowen.com)

一般地，在既定的生产技术条件下若投入和产出之间满足一个函数关系，我们就把这个函数叫作生产函数。这里的生产是一个经济学范畴的概念，含义十分广泛，它不仅仅意味着制造了一台机器或生产出一包豆腐干等，它还包含了各种各样的经济活动，比如会计事务所提供的服务等都是生产的范畴。

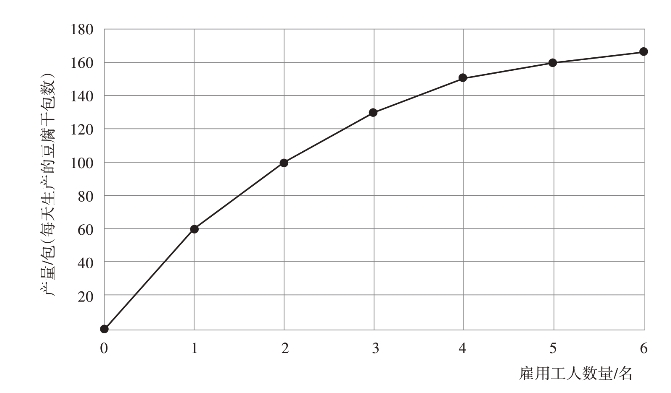
图3-1　石师傅的豆制品厂的生产函数曲线

图3-1就是石师傅的工厂在工厂规模固定的条件下，产量关于工人数量的生产函数。横轴是工人的数量，纵轴是每天生产的豆腐干产量，生产函数图像中两点的斜率表示产量增加量与工人增加量的比值，也就是每增加一名工人的豆腐干产量增加量，即边际产量，斜率越来越小，表明随着工人数量的增加，边际产量递减。

表3-1中的第四列到第七列表示石师傅生产豆腐干的成本，在这个表中可以看到工厂的成本是每天100元，工人的成本是每人每天80元，原材料和包装成本是每包1元，这三项加起来就得到第七列的总成本。同样地，我们将石师傅工厂的总成本关于豆腐干产量的函数关系绘制成图像，就得到总成本曲线。如图3-2就是石师傅豆腐干生产的总成本曲线。根据曲线，我们可以看到，随着产量的增加，总成本曲线越来越陡峭，任意两点连线的斜率越来越大，是因为随着工人数量的增加，由于生产资源的有限（比如数控豆干机没有增加），每增加一名工人，带来的产量增加量越来越少，虽然成本增加量也在不断减少，但产量增加量减少得更快，它与生产函数越来越平缓的原因本质上是一致的，都是边际产量递减。

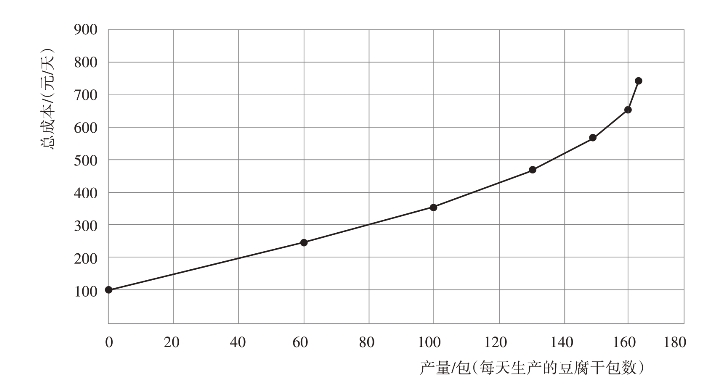
图3-2　石师傅的豆制品厂的总成本曲线