数据分析和数学建模是高中数学两大核心素养，也是数学学习的重点内容和数学能力提升的重要方向。数学建模表现为能够发现和提出问题，通过建立、求解、检验和完善模型，实现分析和解决问题的目标。数据分析是指针对研究对象获取数据，运用数学方法对数据进行整理、分析和推断来获得结论。数据分析主要包括收集数据、整理数据、提取信息、构建模型、进行推断、获得结论。^[2]

经济学也有自己的语言和科学方法。经济学家观察经济现象，并试图与经济理论联系起来，通过假设，使复杂的问题简化，使解释变得容易。经济学家也用图形和方程式的模型来了解世界，帮助分析问题。一方面，经济学和数学有相通的研究方法和思维；另一方面，生动有趣、实用而又广泛存在于日常生活中的经济问题为数学建模和数据分析提供了很好的情景背景和研究对象。当数学模型和经济问题有机结合时，经济数学模型也就产生了。

经济数学模型是经济问题中简化了的各个因素数量关系的数学表达式。它把现实中经济现象的各个因素相互间的关系和人们实践的经验，归纳总结成一套反映数量关系的数学公式和算法，以此来描述经济规律。经济数学模型的种类有很多，从线性模型到非线性模型，各种理论为了解释经济现象衍生出许多数学模型。本书介绍的模型多为线性模型。

构建经济数学模型需要解决几个问题：对生活中经济问题（现象）进行分析、归纳，做出必要且合理的假设；运用数学和经济学思维进行分析，发现数量关系，给出描述问题的数学表述，将经济问题提炼为数学问题；利用数学理论和方法，以及信息技术工具进行分析，得出结论；利用经济案例和数学方法验证结论，并作适当修正。经济数学模型的构建步骤，与数学模型的构建步骤大致相同，一般分为如下七步（如图1-2所示）。

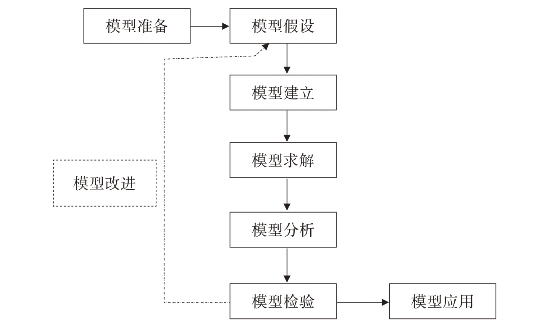
图1-2　构建经济数学模型的步骤

（1）模型准备。

了解生活中经济问题的背景及相关知识，明确需解决的问题，确立经济数学模型构建的目的。同时，对实际经济案例的背景进行细致观察和调研，收集并整理数学建模所必需的信息和数据。

（2）模型假设。

根据所要研究经济问题的特征及建模目的，明确模型中诸多的影响因素，并从中抽象出最本质的问题，对问题做出符合实际情况的、便于用数学语言描述问题的假设。

（3）模型建立。

根据所做出的假设，用数学的语言、符号描述出研究对象的内在规律，并建立包含常量、变量等数量关系的经济数学模型。

（4）模型求解。

结合收集的数据，采用相关的数学原理和方法，应用各种计算工具，对所建立的数学模型进行求解。

（5）模型分析。

根据实际经济问题的原始背景，对求解结果进行分析，包括结果的误差分析、统计分析、模型对数据的灵敏度分析等。

（6）模型检验。

将模型求解分析的结果，与经济现象、实际数据进行比较，检验模型是否符合实际问题，以此来验证模型的准确性、合理性和实用性。若经济数学模型的结果与实际问题不一致，则需返回到模型假设，重复前面的建模过程，直至构建出检验结果符合实际问题的经济数学模型。

（7）模型应用。

模型检验通过后，可将构建的经济数学模型应用推广到合适范围的经济问题中。(www.daowen.com)

例1：（根据2011年贵州贵阳中考题改编）

某玩具厂的龚师傅，生产2件A产品和1件B产品共需50 min；生产1件A产品和2件B产品共需55 min。问龚师傅生产1件A产品需要多少分钟，生产1件B产品需要多少分钟？

解析：

设龚师傅每生产1件A产品、每生产1件B产品分别需要a min和b min，

根据题意，得

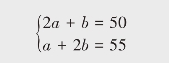
解得

因此，龚师傅生产1件A产品需要15 min，生产1件B产品需要20 min。

这道应用题中就蕴含了一个经济数学模型——生产可能性边界。这个模型清晰地刻画了在外部因素固定时，一个企业（或个人）在一定时间内能够生产的产品数量组合。^[3]按每天工作8 h计算，设龚师傅生产A种产品x件，生产B种产品y件，则x，y满足15x+20y=8×60，即3x+4y=96。做出图像，如图1-3：

图1-3　生产可能性边界模型

龚师傅如果投入全部精力生产A产品，每天将生产32件A产品（生产可能性边界上的A点）；如果投入全部精力生产B产品，则每天能够生产24件B产品（生产可能性边界上的B点）。而实际生产中，龚师傅可能会把一天的时间分配在两种产品的生产中，故在生产可能性边界上就有了其他点（组合）。

由于资源（龚师傅每天能够用于生产的时间、原材料等）是稀缺的，不是每一种组合都可行，实际生产的组合（x，y）需满足约束条件3x+4y≤96。在图像上展示出来，只有在线段AB和两条坐标轴围成区域内的点是生产的可能组合，线段上方的组合不能选取。在线段AB上的所有组合，表明龚师傅获得了生产所需要获取的足够资源，这种情况下的生产是有效率的。反之，线段AB下方的区域，代表的生产结果是无效率的。

生产可能性边界模型反映了一个基本的经济学原理——“理性人”思考机会成本来进行权衡取舍。在边界有效率的点（组合）上，想要生产更多某种产品的唯一方法，就只能是少生产另一种产品。生产可能性边界也表明了用一种产品来衡量另一种产品的机会成本。例如，当生产组合从C（12，15）移动到D（16，12）时，龚师傅多生产了4件A产品，代价是少生产了3件B产品。在C点时，4件A产品的机会成本就是3件B产品，即每件A产品的机会成本等于生产可能性边界的斜率。

图1-3中经济数学模型是简化的模型，生产可能性边界为直线。而现实社会中生产可能性边界往往是凹向原点的曲线，也即每件A产品的机会成本并不是不变的。另外，随着时间推移，生产可能性边界也可能发生变化。比如生产B产品的设备更新，龚师傅能够更快地生产B产品，假设生产1件B产品需16 min，则生产可能性边界方程变为15x+16y=480，如图1-4，说明技术创新（经济增长），经济体可以使生产从原来的生产可能性边界上的一点移动到新的生产可能性边界上的某点。例如，从C（12，15）移动到E（16，15），在保持B产品生产数量相同的情况下，多生产了4件A产品。

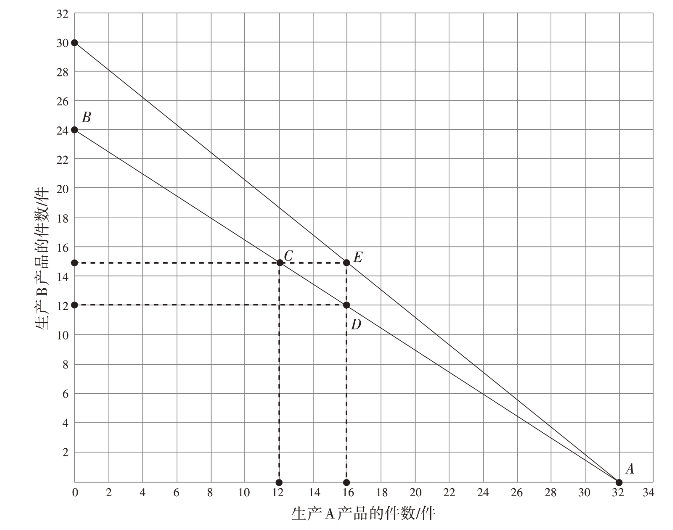
图1-4　生产可能性边界的移动

生产可能性边界模型简化了复杂的经济问题，但表明了机会成本、稀缺性、效率、科技创新等重要的经济概念。这些概念和思想在今后的学习中还会不断出现，生产可能性边界为我们提供了一种思考这些问题的简单模型。

类似生产可能性边界模型，我们会通过典型的经济案例、经济数学模型，学习和了解经济的概念和知识，体会和感悟数学模型的应用，并逐渐掌握构建经济数学模型的方法。