本书利用系统动力学方法对未来人口总数进行预测：①以2010年第六次人口普查数据为基础，将前一年分年龄、性别、城乡的人口数与其对应的生存概率相乘，即可获得后一年分年龄、性别、城乡的自然增长人口数；②将前一年育龄妇女人数（15～49岁）与对应的生育率相乘，获得后一年的新生儿数量（0岁人口）；③考虑城镇化，农村人口迁移到城镇的情况^[1]，能够获得每一年分年龄、性别、城乡的人口数。

“全面二孩”政策的放开刺激妇女生育意愿提高，总和生育率也会提高。我国人口生育政策由独生子女政策向二孩政策的转变，加上全面二孩等政策即将落地，所以本书在人口模型中把生育政策作为可变参数，对不同生育政策下人口数量的变化进行了预测，如表5-1所示。

1）模型假设

i在可预测的时间范围内，未发生由于疫情、灾害或战争等能够导致人口突发变化的事件。

ii本书模型研究中不考虑人口的迁入与迁出行为，是对我国人口自然增长状况的理论模拟。

iii随着“全面二孩”政策的放开后，我国生育率为1．75（并进行极端假设，即生育率＝2时，人口总数及结构的变化。

iv假设出生性别比不发生大的波动。

v假设各年龄阶段的妇女出生概率稳定不变。

vi假设各年龄阶段的人口死亡率及存活率稳定不变。

表5-1　定义与符号说明

2）模型建立

首先，应明确人口系统即为一个老化链结构。因此，按照人口演化的现实规律，按照一定年龄间距对总人口进行分段，本模型以每1岁为一个年龄段，将总人口分为0岁、1岁、2岁、……98岁、99岁及以上，共100个年龄段。根据人口生育的一般规律可知，年龄段在15～49岁的女性人口具有生育能力，于是得到人口系统模型，如图5-1所示。

模型中人口数量没有考虑流动人口的影响，所以，每个年龄段人口的输入流只有两种情况，即新出生的人口，或是从上一个年龄段转化过来的那部分人口。另一方面，每个年龄段人口的输出流有两个：一是转化到下一年龄段的那部分人口，即转移速率（Fi）；二是死亡人口，即死亡速率（FDi）。模型的最终阶段是死亡阶段，即死亡速率。本书所用模型中的生育政策为计划生育政策，将生育政策参数设为调控变量。实行“全面二孩”政策之后，根据资料调查所得的适龄女性的生育意愿强烈程度将生育政策参数设为1．75和2，分析不同政策参数影响下，我国未来总人口的数量及其结构变化趋势。

不同年龄阶段的妇女生育概率不同，通过对统计资料的整理和分析，可得妇女生育时间的分布规律，如表5-2。

表5-2　妇女生育时间的分布规律

以2010年我国第六次人口普查的资料为依据，确定各相关参数和各年龄阶段人口的初始值，并以我国人口普查数据的时点为初始状态，利用100阶段构建人口系统仿真模型进行系统仿真，如图5-1所示。

3）我国人口系统动力学模型中的变量与方程说明

由于此模型中涉及的变量比较多，为方便清晰阐述模型各组成部分，将分别解释模型中变量及方程的经济含义。

首先将系统动力学中方程的构成及通用符号的含义做出说明。

（1）女性人口（FPi）。

图5-1　我国人口系统模型

[状态方程]：FPi＝Fi-1-FDi-Fi

其中：

FDi：第i年龄段的女性人口死亡速率；

Fi：第i到第i+1年龄段的女性转移速率。

决策方程：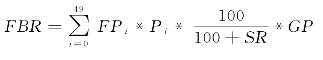

其中：

FBR：女性出生速率；

FPi：第i年龄段的女性人口；

Pi：第i年龄段女性的生育概率；

SR：新生儿出生性别比；

GP：生育模式。

辅助方程：FDi＝FPi∗FDRi；Fi＝FPi∗（1-FDRi）

其中：

FDRi为第i年龄段的女性人口死亡率。

（2）男性人口（MPi）。

[状态方程]：MPi＝Mi-1-MDi-Mi

其中：

MDi第i年龄段的男性人口死亡速率；

Mi第i到第i+1年龄段的男性转移速率。(www.daowen.com)

决策方程：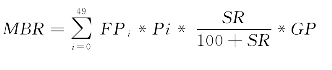

其中：

MBR：男性出生速率；

FPi：第i年龄段的女性人口；

Pi：第i年龄段女性的生育概率；

SR：新生儿出生性别比；

GP：生育模式。

辅助方程：MDi＝MPi∗MDRi；Mi＝MPi∗（1-MDRi）

其中：

MDRi：第i年龄段的女性人口死亡率。

（3）总人口。

在人口系统模型基础上，我们继续构建出总人口子系统模型及说明如下。

总人口子系统是总人口数量的仿真模拟。总人口数量等于各年龄段人口数量之和，其模型如图5-2所示。

图5-2　总人口子系统模型

其中：

TPi：某年龄段人口数量。

决策方程：TPi＝FPi+MPi

其中：

FPi：第i年龄段的女性人口；

MPi：第i年龄段的男性人口。

辅助方程：FPi＝Fi-1-FDi-Fi；MPi＝Mi-1-MDi-Mi

其中：

FDi：第i年龄段的女性人口死亡速率；

Fi：第i到第i+1年龄段的女性转移速率；

MDi：第i年龄段的男性人口死亡速率；

Mi：第i到第i+1年龄段的男性转移速率。

1）未实行“全面二孩”政策情景下人口系统仿真分析

情景一：当前生育政策参数＝1．6，在该情境下，预测2010—2050年人口变化趋势，作为参考对象。

“全面二孩”政策已经放开，做如下假设：

情景二：未来几年，符合条件的适龄妇女生育意愿较强烈，生育政策参数＝1．8。

情景三：“全面二孩”政策下，符合条件的适龄妇女生育意愿非常强烈，生育政策参数＝2。

各种情景下，人口仿真分析结果如下。

2）人口总数及结构预测

不同情境下，总人口数以及各年龄阶段的人口总数的变化趋势如图5-3所示。

在这三种情境下，总人口数量在预测期间都呈先升后降趋势。在情景一中，人口总数在2028年达到峰值，之后开始逐年下降。在情景二中，总人口数量在2031年达到峰值，之后开始逐渐下降。在情景三中，总人口数量在2049年达到峰值，之后逐步下降，如表5-3所示。

图5-3　不同情境下人口总数预测图

表5-3　不同情境下人口结构预测

（续表）