1）数据预处理

由于很多变量为连续型变量，需对其进行离散化处理。为了贝叶斯网络条件概率的确定，本研究根据每一个变量的分布特征，将所有变量的取值离散化为低、中、高三级，分别用1、2、3表示。离散化结果如表5－8所示。

法规政策变动风险、行政限制与歧视风险、政治暴力风险、贪污腐败风险、政府违约风险、针对项目的抗议风险分别用F1、F2、F3、F4、F5、F6代表。

表5－8　变量离散化结果

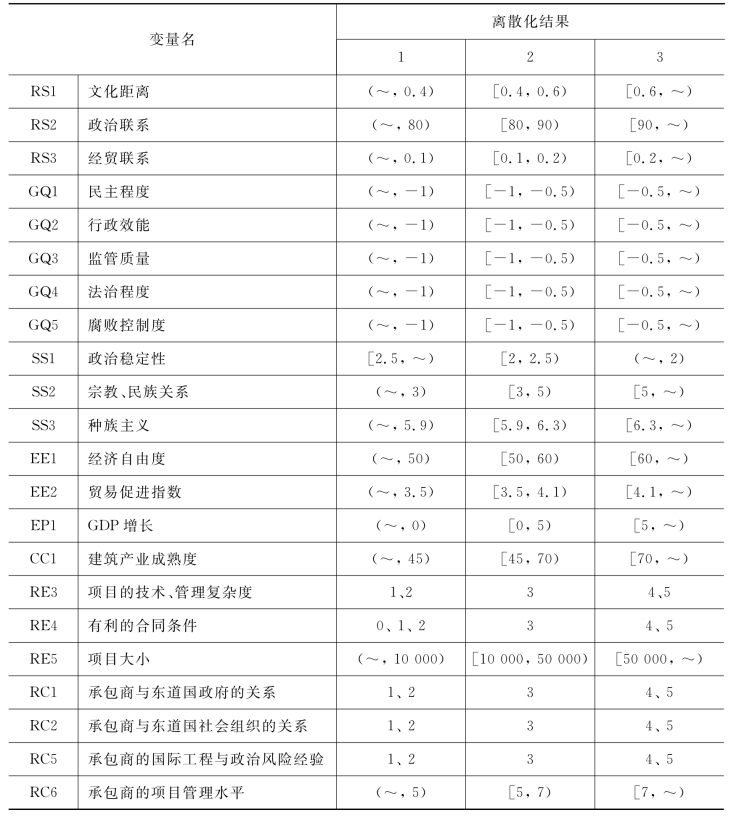
2）参数学习

目前在贝叶斯网络的应用中，条件概率多由专家直接给出，再通过相应案例不断更新，以这种方式计算最终的概率值。但是，在贝叶斯网络复杂的关联关系之下，专家很难根据经验制定其中的条件概率。一旦节点非常多，在关联关系复杂的情况下，预设条件概率就变得更难实现了。因此，本研究通过网络参数学习的方式确定各节点的条件概率。

贝叶斯网络参数学习算法主要有三种方式：最大似然估计法，贝叶斯估计法，梯度下降算法，以及期望最大算法。其中前两种算法用于没有缺失值的情况下，而后两种算法通常用于存在缺失值的算法中。本研究所涉及的样本不存在数据缺失的情况，因此本研究采用贝叶斯估计法进行参数学习。

贝叶斯估计假定一个固定的未知参数θ，考虑给定拓扑结构S下，参数θ的所有可能取值，利用先验知识，寻求给定拓扑结构S和训练样本集D时具有最大后验概率的参数取值（Fayyad，等，1996；慕春棣和戴剑彬，2000）。给定拓扑结构S和训练样本集D时，贝叶斯网络的后验概率为P（θ｜D，S）。采用最大后验概率方法对贝叶斯网络参数θ∧进行估计，可以描述为：

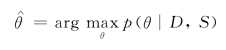
由贝叶斯规则可以得出：

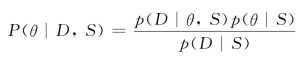
其中，p（θ｜S）为拓扑结构S下参数θ的先验概率，p（D｜S）与具体参数取值无关。通常使用先验分布是狄利克雷分布。考虑多项式的参数为：θ1，θ2，…，θk，∑θi＝1，狄利克雷分布为一组超参数α1，α2，…，αk，当P（θ｜D，S）满足狄利克雷分布时，参数θ的后验概率为：

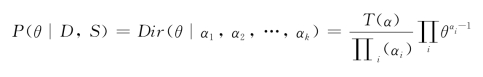
对于数据集合D，统计值为：N1，N2，…，Nk，则(www.daowen.com)

将这一结果推广到贝叶斯网络，定义事件V，其节点为v，父节点Pa（v）＝u，统计值记为N（v，u）。在贝叶斯估计算法中，参数估计由下式计算：

本研究的样本集共包含301个样本，从中随机挑选10%（即30个）样本用于鲁棒性检验。因此本研究的训练样本集共包含271个样本。

使用Netica软件进行贝叶斯网络的样本训练，训练结果如图5－7所示。

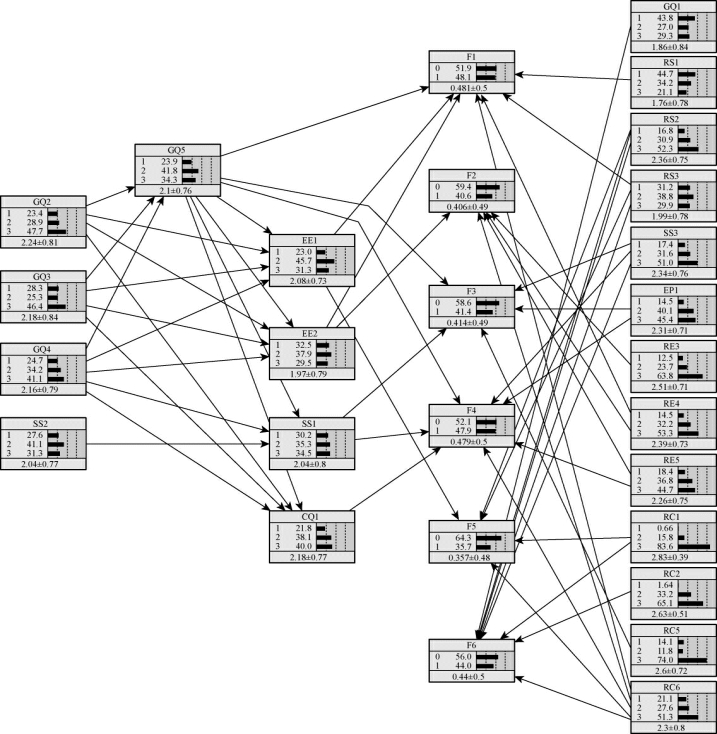
图5－7　国际工程政治风险预测的贝叶斯网络参数学习结果

3）鲁棒性检验

本研究已随机挑选出30个样本作为测试集，用来验证国际工程政治风险预测的贝叶斯网络参数学习的鲁棒性。预测概率大于等于50%，视为该种类型的政治风险预测结果为发生；预测结果小于50%，视为该种类型的政治风险不发生。通过对比模型预测结果与案例的实际结果，计算模型预测的准确率。例如，对于测试案例2，预测结果为F1、F2发生，F3、F4、F5、F6不发生；而实际结果为F2发生，F1、F3、F4、F5、F6不发生，模型对案例2中F1的预测结果错误，对F2、F3、F4、F5、F6的预测结果无误，即，该预测模型对测试案例2的政治风险预测准确率为83.3%。模型对所有测试案例的预测结果见表5－9。

表5－9　鲁棒性检验结果

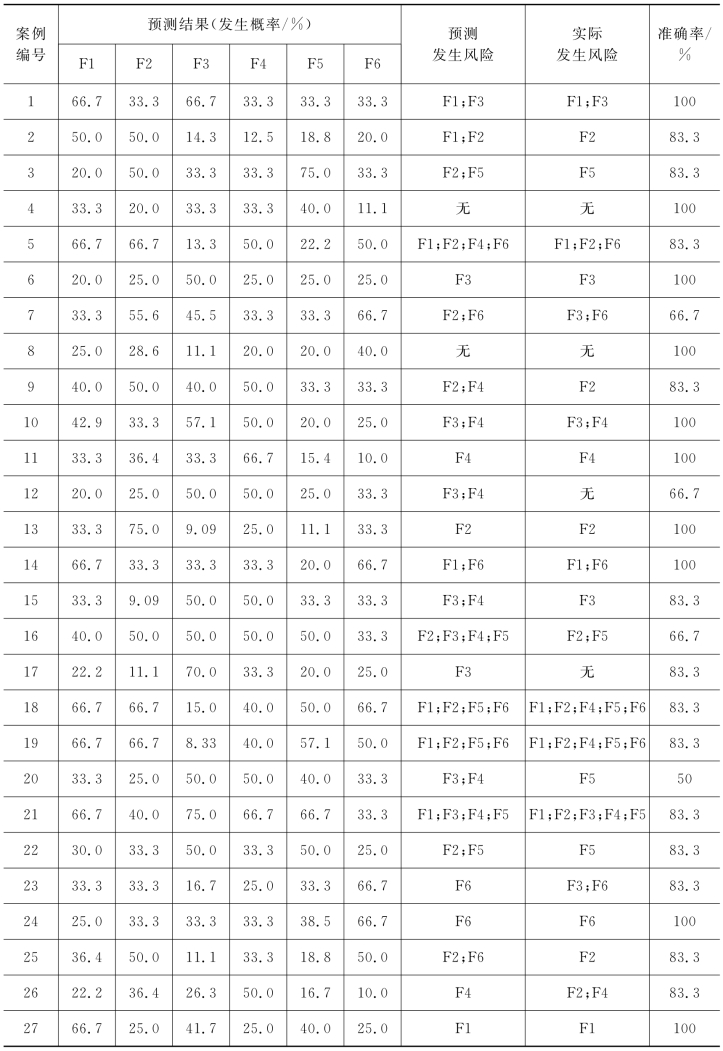
续表

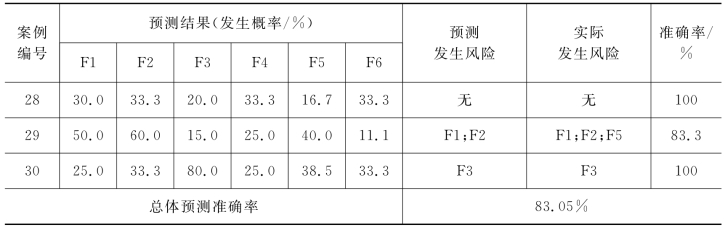
由表5－9可知，该国际工程政治风险预测模型对30个测试案例的总体预测准确率为83.3%。表明该预测模型预测结果具有较高的指导意义，鲁棒性较好。