贝叶斯网络是一种基于贝叶斯推理的风险量化方法（Heckerman，1997），也称为信度网络、因果网络或者推理网络，是由概率变量、节点和其间的有向连接构成。在这个网络中，原因和结果变量都用节点表示，节点也可以是任何问题的抽象，变量之间的相关或推论关系以有向连接表示，同时每个节点有一组有限的排他的状态，其似然分配表示为信度值。网络中节点的信度值表示事件本身的不确定性，条件概率则可以有效表示专家经验知识具有的不确定性。应用贝叶斯网络中对节点事件进行推理的方法是通过输入证据，节点的后验信度值被更新而实现的。

贝叶斯概率网络是一种数据推导，利用先验知识以及样本数据来获取对未知样本的评估。联合概率及条件概率则是先验信息以及样本数据信息的表现形式。

假设有n个互斥、全覆盖事件A1，…，An。若P（A1）表示事件A1的发生概率，则有，设B为任一事件，有：

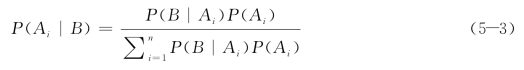
公式（5－3）即为贝叶斯公式。其中P（A1）为先验概率。例如在实验中，事件B的发生，对事件Ai的发生可能有新的认识，概率P（Ai｜B）为后验概率。后验概率不仅综合了先验信息，也综合了试验中获得的新信息，所以能对Ai发生的可能性进行判断，而先验信息到后验信息的转化是贝叶斯统计最显著的特征。贝叶斯网络以有向无环图的形式对系统进行建模，用节点表示系统中的变量，用有向边表示变量之间的因果关系，用条件概率表示变量之间的相关程度，其可以表达和分析多源信息，进而处理不确定性问题。

贝叶斯网络也称因果网络或概率网络，这两个名称也从侧面反映了贝叶斯网络的图属性和概率属性。贝叶斯网络就是将概率关系赋值到表达因果关系的有向无环图中，形成能够表示变量间依赖关系的概率图，一般由结构和参数两部分组成，结构也就是其图形结构，即所谓的“有向无环图”（Directed Acyclic Graph）。贝叶斯网络中的节点表示因素和事件，也称作贝叶斯网络的变量。各变量之间的依赖关系，即事件之间的直接因果关系用节点间的有向弧表示，表示原因的节点称为“父节点”，表示结果的节点称为“子节点”。图5－2中，节点E1直接影响到节点E2，即E1→E2，建立节点E1到E2的有向弧（E1，E2），则E1为E2的父节点，E2为E1子节点。

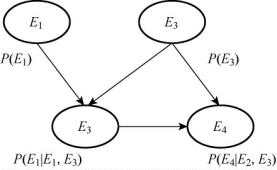
图5－2　贝叶斯网络示意图

贝叶斯网络的参数是指变量的条件概率分布。贝叶斯网络通过条件概率将变量对其父节点的依赖关系定量化，也可以称作弧的连接强度，体现了变量之间的直接相关性和条件相关性。每个子节点变量的参数用其在父节点取值状态下的条件概率表示，每个根节点的参数则使用边缘分布。节点E1、E2、E3、E4分别代表不同的事件，E1、E3属于根节点，也是E2的父节点，E4是E2和E3的子节点。E1和E3的参数分别由其边缘分布P（E1）、P（E2）表示；子节点E2的参数则通过P（E2｜E1，E3）表示，即在E1、E3发生的情况下，事件E2的发生概率。从这一表达方式也可以推知事件E1、E2、E3之间存在着一定的因果关系。

贝叶斯网络基于条件独立性假设，节点的条件概率如式（5－4）所示。(www.daowen.com)

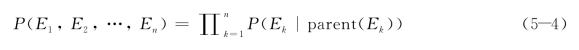
贝叶斯网络具有以下的一些特点：

（1）条件独立性：由于贝叶斯网络假定条件独立性，在求变量的概率信息时，只需要考虑与该变量有关的有限变量，这就大大简化了问题的求解难度，从而使得许多复杂问题得到可行的解决方法。

（2）基于概率论的严格推理：贝叶斯网络是一种不确定性知识表达与推理模型，它的推理原理基于贝叶斯概率理论，推理过程实质上就是概率计算。节点的条件概率主要来源于专家经验、专业文献和统计学习。

（3）知识获取与推理的复杂度较小：由于贝叶斯网络具有条件独立的特点，因此可以减少知识获取与推理的复杂程度。也就是说，在知识获取时，只要关心与节点相邻的局部网络图；在推理计算时，只要已知节点的相关节点的状态即可估计该节点的概率信息。

与传统进行风险分析采用的故障树方法相比，贝叶斯网络作为一种图形化的建模工具，具有一系列的优点：①贝叶斯网络将有向无环图与概率论有机结合，不但具有正式的概率理论基础，同时也具有更加直观的知识表示的形式；②同一分析模型中既可包含定性的变量，又可包含定量的变量；事件的状态描述不仅限于正常和失效两种状态的描述，它可以描述事件的各种可能存在的状态以及变量独立及相关状态的相容性，可以解决共因失效问题；③贝叶斯网络节点之间是相互影响的，任何节点观测值的改变都会对其他节点造成影响，并可利用贝叶斯网络推理功能来进行估计和预测；④贝叶斯网络能够识别必需的和不相关的信息，利用条件独立性排除高冗余对称结构，使得网络数随着问题规模线性增长，网络结构比较紧凑。

贝叶斯网络的推理并不局限于只顺着弧的方向推理。贝叶斯网络将一个联合概率分布直观地表达为一个图形结构和一系列的条件概率表，在已知某些变量取值的情况下，可以计算出感兴趣的节点变量的条件概率分布。最基本和最主要的推理形式有以下两种：

（1）预测推理：是由原因推导出结果。贝叶斯网络可以充分利用变量之间的依赖信息进行预测，当已知一定的原因（证据），经推理计算，可求出在该条件下结果的概率分布。在本研究中可以理解为根据已知政治环境中一些变量的特征，预测更有可能发生什么样的风险。

（2）诊断推理：是由结论来推知原因。目的是在已知结果时，找出产生该结果的原因。当已知某些结果的发生，经推理计算，可得出造成该结果发生的原因及其发生的概率，在本研究中可以理解为根据已经发生的政治风险的特征，推理政治环境的变化，寻找风险致因。

贝叶斯网络的以上特性非常适合用于对事件的发生发展过程进行建模分析，适合于表达与事件发生发展相关的各种因素之间的复杂关联关系，适合于描述因素多态性以及因素间逻辑关系非确定性。通过概率推理，能够对事件的整个发生发展过程进行定量的分析预测。因此本书选择贝叶斯网络作为建模工具，对因素和事件形成的因果关系网络进行定量分析。