结构方程模型（Structural Equation Model，SEM）作为一种多元统计技术，是一种运用统计中的假设检验方法对有关现象的内在结构理论进行分析的一种统计方法，产生后迅速得到了普遍的应用（Finch，2009）。其应用起于20世纪60年代，20世纪70年代初一些学者将因子分析、路径分析等统计方法整合，提出结构方程模型的初步概念。随后Joreskog与其合作者进一步发展了矩阵模型的分析技术来处理共变结构的分析问题，提出测量模型与结构模型的概念，促成结构方程模型的发展。在社会科学以及经济、市场、管理等研究领域，有时须处理多个原因、多个结果的关系，或者会碰到不可直接观测的变量（即潜变量），这些都是传统的统计方法不能很好解决的问题。结构方程模型的最大优势就是引入了潜变量，并且具有可以同时处理多个因变量，容许自变量和因变量含测量误差，同时估计因子结构和因子关系等优点。正因为如此，结构方程模型开始在心理学、教育学、社会学、经济学等领域得到了广泛的应用。

为了更清晰地阐述结构方程模型和传统的统计方法的区别，现对三种分析方法进行对比分析。

线性相关分析：线性相关分析指出两个随机变量之间的统计联系。两个变量地位平等，没有因变量和自变量之分。因此相关系数不能反映单指标与总体之间的因果关系。

线性回归分析：线性回归是比线性相关更复杂的方法，它在模型中定义了因变量和自变量。但它只能提供变量间的直接效应而不能显示可能存在的间接效应。而且会因为共线性的原因，导致单项指标与总体出现负相关等无法解释的数据分析结果。

结构方程模型分析：结构方程模型是一种建立、估计和检验因果关系模型的方法。模型中既包含有可观测的显在变量，也可能包含无法直接观测的潜在变量。结构方程模型可以替代多重回归、通径分析、因子分析、协方差分析等方法，清晰分析单项指标对总体的作用和单项指标间的相互关系。

简单而言，与传统的回归分析不同，结构方程分析能同时处理多个因变量，并可比较及评价不同的理论模型。与传统的探索性因子分析不同，在结构方程模型中，我们可以提出一个特定的因子结构，并检验它是否吻合数据。通过结构方程多组分析，我们可以了解不同组别内各变量的关系是否保持不变，各因子的均值是否有显著差异。目前，已经有多种软件可以处理SEM，包括：LISREL，AMOS，EQS，Mplus。

结构方程模型可分为测量方程（Measurement Equation）和结构方程（Structural Equation）两部分，测量方程主要表示观测变量和潜变量之间的关系，其表达式通常写为（成子娟，等，2006）：

(www.daowen.com)

其中，x为外生观测变量向量；y是内生观测变量所构成的向量；Ax是外生观测变量在外源潜变量上的因子负荷；Ay是内生观测变量在内生潜变量上的因子负荷；δ是外生变量x的误差向量；ε是内生变量y的误差向量。

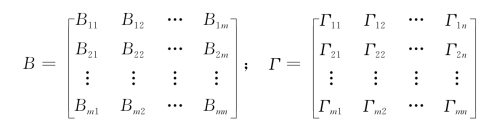
结构方程主要表示潜变量之间的关系，其表达式通常写为：

其中，η是内生潜变量向量，ξ是外生潜变量向量；B是内生潜变量η的系数矩阵；Γ是外生潜变量ξ的系数矩阵；ζ为结构方程的残差项，表示模型内未能解释的部分。

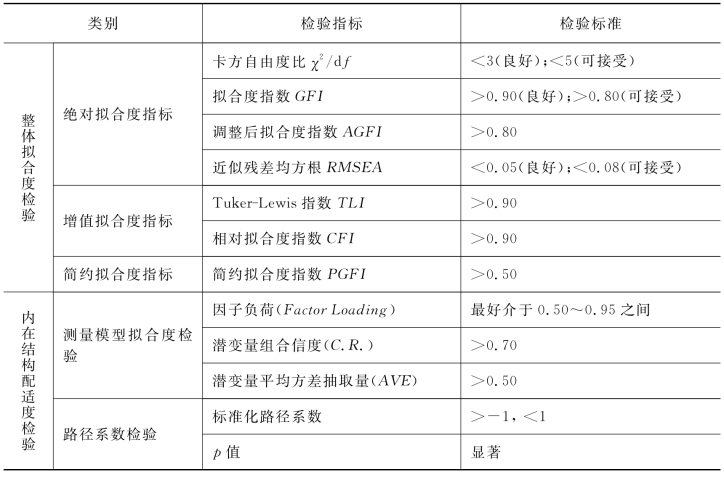
SEM的核心在于评价理论假设模型与样本数据是否契合，如果出现拟合不佳，须在兼顾理论合理性的前提下，对假设模型修正以达到拟合度要求。一般从整体拟合度和内在结构配适度两个方面评价模型的拟合度。具体拟合度的检验指标和检验标准如表4－6所示。在拟合度评价之前，需要先检验模型是否违反估计，包括模型解中出现负的误差方差、路径系数大于1或小于－1、协方差矩阵或相关矩阵不正定。如果存在上述情况，说明模型存在错误。

表4－6　模型拟合度检验指标及标准