对象选择是价值工程的第一个基本步骤，也是进行价值工程研究中所面临的第一个挑战。特别是对于那些进行价值研究有着资金限制，或者仅仅因为有太多的潜在对象而不能做出选择的大机构来说，就非常有必要仔细考虑并选择那些可能获得最大的投资收益的对象。在选择对象的过程中，主要采取以下几种方法。

1) ABC分析法

ABC分析法也称成本比重分析法或帕累托(Parete)分配律法。帕累托是意大利经济学家，他在研究资本主义国民财富的分配状况时，发现这样一个分配规律：占人口比例不大的少数人占据社会财富的大部分。后来，人们把这种不均匀分配规律用于成本分析、库存管理分析等许多经营管理问题中。将帕累托分配律应用于产品成本分类上，通过成本分析可以发现：占零件总数10%左右的零件，其成本往往占整个产品的60%～70%，这类零件可划为A 类；占零件总数20%左右的零件，其成本也占总成本的20%，这类零件可划为B 类；占零件总数70%左右的零件，其成本仅占总成本的10%～20%，这类零件可划为C类，如图17-4所示。人们利用这种分类的办法，可以实现对零件的分类控制。这就是ABC分析法。

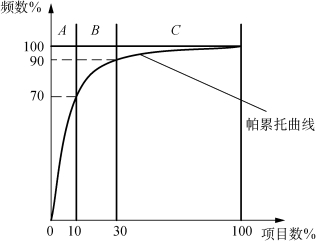
图17-4　帕累托曲线

当产品不是可分的机械产品，而是矿产、冶金、化工和纺织等不可分的连续产品或工艺时，我们可以从成本构成的角度进行分类，如分为材料费、动力费、工时费及折旧费等，并计算出各类费用所占总费用的百分比重，把比重大的项目作为A 类对象予以选择。ABC法是最常用的一种方法，它的优点是能抓住重点，把数量少而成本大的零件或工序选为价值工程对象，利于集中精力，重点突破，取得较大成果。这一方法的缺点，在于有时现实成本虽属C类，但功能却十分重要，开展价值工程很有潜力，然而却未被选为对象。因此，在采用此法的同时，最好结合其他方法来综合分析，避免应入选的对象未被选中。

2) 百分比法(费用比重分析法)

这种方法是通过分析各个产品的两个或两个以上的技术经济指标所占的百分比来选定分析对象的。例如，某厂有六个产品，它们的成本和利润的百分比如表17-3所示。

表17-3　某厂产品成本利润百分比表

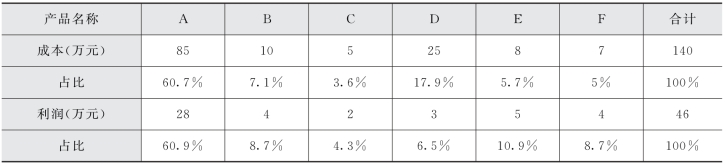
由上表可知，D 产品的成本占总成本17.9%，而利润只占总利润6.5%。因此，应选择D 产品作为价值工程重点对象。

3) 最合适区域法

最合适区域法最早由日本的田中教授提出，是对价值系数判别法的改进。即使两个零件价值系数相同，其成本系数和功能系数的绝对值往往也不相同，因而在选择价值工程的对象时，不能简单地把价值系数相同的对象同等看待，而要优先选择对产品实际影响大的对象。例如，某产品有A、 B、 C、 D 四个零部件，有关数据见表17-4。

表17-4　某产品相关数据(www.daowen.com)

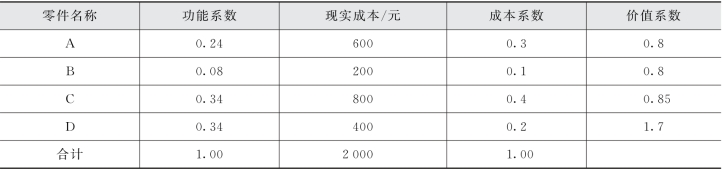
在该产品中，零件A 与B价值系数相同。但是，若把二者的价值系数都提高到1，则A零件可使成本降低120元，而B产品只能使成本降低40元，因此优先选取A 零件作为价值工程的对象更为合理。另外，虽然C零件的价值系数高于B零件，按照价值系数判别法应该优先选B零件作为价值工程对象。但是，将B零件的价值系数提高到1，总成本降低40元，而将C零件选为价值工程的对象，可使总成本降低120元，因此应优先选取C零件作为价值工程的对象。由此可见，不能仅依据价值系数选择价值工程的对象，还应该综合考虑功能系数与成本系数的绝对值，严格控制功能系数和成本系数过大的对象，保证不漏掉重点对象。

最合适区域法正是基于这一原理提出来的对象选择方法。所谓最合适区域，就是指成本系数和价值系数匹配的区域，落在这一区域内的对象，即使价值系数偏离1也可以不选为价值工程的对象。

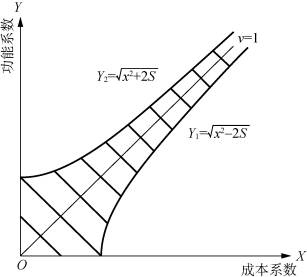
图17-5　最合适区域法

最合适区域的画法如下：以成本系数为横坐标，功能评价系数为纵坐标，则与X 轴或 Y 轴夹角为45°的直线即为价值系数为1的标准线V=1；再以 作两条曲线，两条曲线所包络的阴影部分即为最合适区域。如图17-5所示。

只要确定了常数S 的值，就可以在坐标图中画出最合适区域。S 的取值是否恰当，决定了最合适区域的可信度。在实践过程中，可以多次试验，代入不同的S 值，直到获得满意的结果。

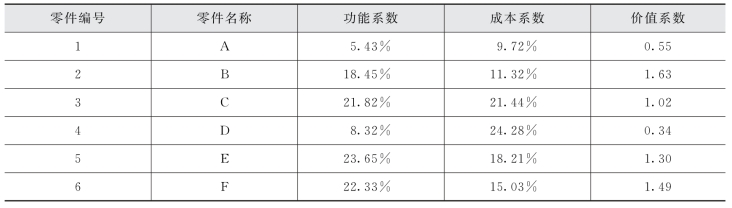
例如，某产品有5个零部件，各零部件的功能系数、成本系数、价值系数如表17-5所示。

表17-5　某产品功能系数、成本系数、价值系数表

通过多次试验，最终取S=50，在坐标上做出 两条曲线，得到最合适区域，如图17-6所示。

图中，A、 C 都在最合适区域内，可以不作为价值工程的对象，B、 D、 E、 F 都在最合适区域外，特别是D 零件，远离最合适区域，可选为价值工程的对象。

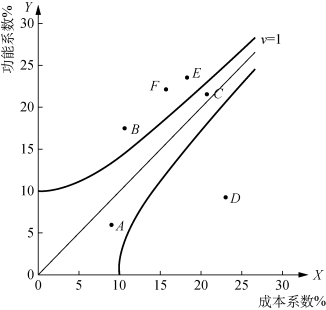
图17-6　最适合区域与对象选择