风险是指损失发生的不确定性（或可能性），所以风险是不利事件发生的概率及其后果的函数，而风险估计就是估计风险的性质，估算风险事件发生的概率及其后果的严重程度，以降低其不确定。

概率是度量某一事件发生的可能性大小的量，它是随机事件的函数。必然发生的事件，其概率为1，记为P（U）=1，其中U代表必然事件；不可能事件，其概率为零，记为P（V）=0，其中V代表不可能事件；一般的随机事件，其概率在0与1之间，记为0≤P（A）≤1，A代表任一随机事件。

使用概率分析方法衡量风险大小，需要知道风险事件的发生概率和后果。例如，修建核电站和火电站，哪一种环境风险大呢？核电站事故的后果虽然严重，但发生严重事故的概率很小；火电站排放烟尘和污水虽然短时间不会成灾，但是每天都排放，污染环境的概率却是百分之百的。因此，衡量风险的大小，必须综合考虑风险事件发生的概率和后果严重性。风险事件的发生概率和后果严重程度的乘积可叫作风险事件状态。因此，风险的大小可由风险事件状态来计量。

概率分布是概率论的基本概念之一，用以表述随机变量取值的概率规律。为了使用的方便，根据随机变量所属类型的不同，概率分布取不同的表现形式。简单地说，概率分布是显示各种结果发生概率的函数。风险估计中常用的概率分布有离散分布、等概率分布、泊松分布、二项分布、威布尔分布、正态分布和对数正态分布等。风险事件发生的概率和概率分布是风险估计的基础，因此，风险估计的一个重要方面是确定风险事件的概率分布。在风险估计中，概率分布用来描述各种损失发生可能性大小的分布情况。研究概率分布时，需要注意充分利用已获得的各种信息进行估测和计算，在获得的信息不够充分的条件下则需要根据主观判断和近似的方法来确定概率分布，具体采用何种分布应根据项目风险的特点而定。

风险估计的首要工作是确定风险事件的概率分布。在对风险事件进行历史统计时，常常会遇到两种不同类型的随机变量。当某随机变量全部可能取到的值是有限或无限个时，称其为离散型随机变量。例如，在相同条件下抛掷同一枚硬币，其结果要么是硬币正面朝上，要么是反面朝上，只能有这两种结果。又如，统计一个驾驶员在某一年中发生交通事故的次数的概率，0次的概率是0.65，1次的概率是0.20，2次的概率是0.05，一年内所发生的交通事故次数总是有限的。这些事件发生的结果都是可数的，都是离散型随机变量。

当某随机变量全部可能取到的值是一个区间，是无法按一定次序一一列举出来的时候，称其为连续型随机变量。例如，某种电器产品的使用寿命就是一个随机变量，它的使用寿命在1000～1500小时范围内连续变化，也就是说，随机变量可以是在［1000，1500］这样一个区间内的任何值，可能出现的结果是不可数的。这一类随机变量，通常被称为连续型随机变量。

总之，可用随机变量来表示风险所致损失的结果，该随机变量的概率分布就是风险事件的概率分布。从风险事件的概率分布可以得到期望值、标准差、差异系数等统计信息，这些信息对于衡量风险大小是非常有用的。

确定风险事件的概率分布一般有三种方法：根据历史资料确定风险事件的历史概率分布法、理论概率分布法和主观概率分布法。一般来讲，风险事件的概率分布应当根据历史资料来确定，但当项目管理人员没有足够的资料来确定风险事件概率分布时，也可以利用理论概率分布进行风险估计。

在实际工作中，可假设某个风险事件发生的概率满足某种分布，并通过历史数据进行分析，得到其概率分布的表达式，最终求出风险事件发生的概率。下面通过一个例子来说明如何采用历史统计资料来确定一个风险事件的概率分布。

例4-1　假设建设项目实际要用的时间是一个服从正态分布的随机变量。例如，某建筑公司在过去8年中完成了72项工程施工任务。有些项目提前完成，而另一些则由于种种原因而拖延工期。为了估计今后承包工程时工期拖延的风险，公司管理人员将这些工程拖延的情况整理了出来并列在表4-1中。工期拖延的情况用拖延的时间占计划工期的百分比表示，负值表示任务提前完成。

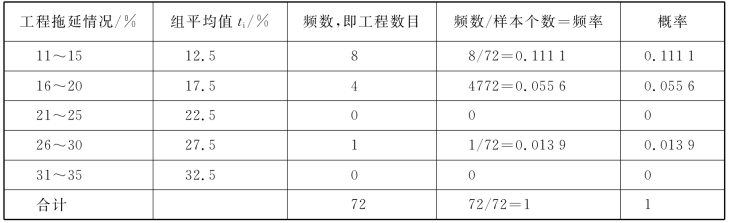
表4-1　工程拖延情况统计(www.daowen.com)

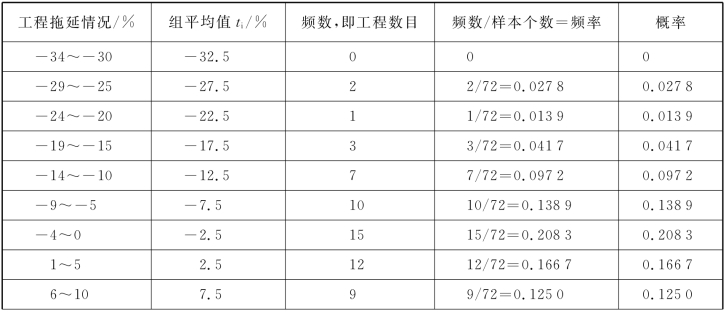
续表

若把表4-1中的样本分布用条形图表示出来，可得图4-1。图4-1叫作直方图。纵坐标表示工期拖延的频率，横坐标表示拖延的时间占计划工期的百分比。根据直方图，可以大致画出拖延时间的概率密度曲线，如图4-1中实线所示。

当样本个数足够多时，例如，把与该公司情况类似的其他公司过去8年中完成的工期数据也拿来比较分析，工期拖延时间的概率密度曲线的形状就接近于图4-1中的虚线。这条虚线表示的即为正态分布。

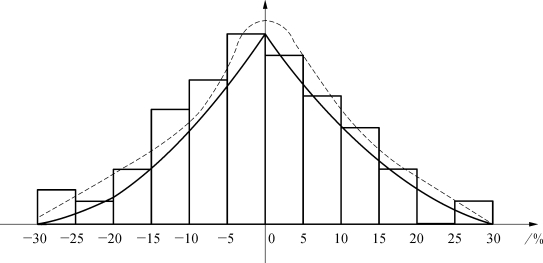
图4-1　工期拖延的直方图

假设公司有一个新工程要承包，计划工期是16个月，项目管理人员要了解工期拖延超过4个月的概率，则可先算出工期拖延的随机变量取值为4／16×100%=25%。采用这些数据，可分别通过直方图和近似的正态分布曲线进行分析。

若采用直方图分析，则可根据表4-1中的数据，计算工期拖延大于25%的概率，即为拖延工期26%～35%的概率。于是得到：

（0.0139＋0）×100%=1.39%

于是可得，工期拖延超过4个月的概率是1.39%。