向量自回归模型(Vector Autoregressive Model)通常采用多方程联立的形式，它是由西姆斯Sims在1980年提出并后续逐渐得以发展。向量自回归模型并不强调必须借助于经济理论。在模型的每一个方程中，内生变量都会形成滞后回归效应，既对自己也对其他内生变量产生影响，通过估计全部内生变量的动态关系来分析内生变量的作用问题。西姆斯指出VAR模型中的全部变量都是内生变量。近年来也有学者作出了更多的探索，越来越多的研究指出具有单向因果关系的变量，也可以作为外生变量加入VAR模型。

向量自回归VAR模型具有以下五个特点:

第一，不依赖于严格的经济理论。在构建向量自回归模型时，需要明确两个前提: 一是变量间的相互影响关系。确定共有哪些变量是存在相互影响的，并把有关系的变量放入向量自回归VAR模型中。二是确定滞后期k。变量间的相互影响关系与滞后的期数有密切的联系，因此，构建模型时首先需要确定滞后期数。

第二，对任何参数施加零约束不能应用于向量自回归VAR模型中。无论参数估计值是否显著，都应保留在模型中。

第三，任何当期变量对其他变量的影响是不在考虑范围中。

第四，向量自回归VAR模型需要估计很多参数。例如，假定向量自回归VAR模型中含有三个变量，通过分析后发现滞后期数为5，那么估计的参数数量则有75个，kN2=3 52=75。在样本容×量较小的情况下，参数的估计会带来更多问题，尤其是误差会增加许多。

第五，无约束向量自回归VAR模型主要应用于预测。无约束的模型不需要考虑当期变量的影响，因此在预测时有很大的应用空间，避免了当期数据的收集以及影响的讨论，这是向量自回归模型最大的优点。

向量自回归VAR模型的原理。我们将深入分析向量自回归模型，这种模型更适合于估计和预测。由于Sims(1980)在经济中的出色运用，向量自回归模型在分析经济系统的动态性上得到了广泛的应用。

1. 无限制向量自回归模型的极大似然估计和假设检验

按照时间序列模型极大似然估计方法，我们首先分析向量自回归模型的条件似然估计。

(1)向量自回归模型的条件似然函数。

假设yt表示一个包含时间t时n个变量的n×1的向量。假设yt的动态过程可以由下面的p阶高斯向量自回归过程:

yt=c+Φ1yt-1+Φ2yt-2+…+Φpyt-p+εt，εt～N(0，Ω)

假设我们已经在(T+p)个时间间隔中观测到这些n个变量的观测值。如同标量过程时的情形，最简单的方法是将前p个样本(表示为y-p+1，y-p+2，…，y0)作为条件，然后利用后面的T个样本(表示为y1，y2，…，y T)形成参数估计。我们的目的是构造下面的条件似然函数:

这里参数向量为θ=(c，Φ1，Φ2，…，Φp，Ω)，我们在上述函数中相对于参数θ进行极大化。在一般情形下，向量自回归模型是在条件似然函数基础上，而不是在无条件似然函数基础上进行估计的。为了简单起见，我们将上述“条件似然函数”称为“似然函数”，相应的“条件极大似然估计”称为“极大似然估计”。

向量自回归与标量自回归过程的似然函数的计算方法是类似的。基于时刻t-1以前观测值，时刻t的yt值等于常数向量: c+Φ1yt-1+Φ2yt-2+…+Φpyt-p，加上一个多元正态分布的随机向量εt～N(0，Ω)，因此条件分布为:

我们可以将上述条件分布表示成为更为紧凑的形式。假设向量xt是常数向量和yt滞后值向量构成的综合向量:

xt≡(1，y't-1，…，y't-p)'

这是一个维数为［(np+1) ×1］的列向量。假设Π'表示下述［n ×(np+1)］维矩阵:

Π'≡［c，Φ1，Φ2，…，Φp］

这时条件均值可以表示为Π'xt，Π'的第j行包含VAR模型第j个方程中的参数。使用这样的符号，我们可以把条件分布表示成为紧凑形式:

因此第t个观测值的条件分布可以表示为:

这是基于条件{y0，y-1，…，y-p+1)的观测值从1到t的联合概率分布为:

连续迭代利用上述公式，可以获得全部样本y T，y T-1，…，y1基于{y0，y-1，…，y-p+1)的联合条件分布是单独条件密度函数的乘积:

因此，样本对数似然函数为:

(2)Π的极大似然估计。

我们首先考虑Π的极大似然估计，它包含常数向量c和自回归系数Φj。我们的结论是它可以利用下述公式给出:

这可以当做yt基于常数和xt母体线性投影的样本估计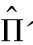，的第j行是:

这正是yjt基于常数和xt进行线性回归的普通最小二乘估计(OLS)的估计系数向量。因此，VAR模型第j个方程系数的极大似然估计可以从yjt基于常数项和该系统所有变量的p阶滞后变量进行线性回归得到的OLS估计获得。

为了验证上述结论，我们将似然函数中的最后一项表示为:

这里的n×1向量的第j个元素是从yjt基于常数和xt进行线性回归得到的观测值t的样本残差:

进一步将上式化简为:

考虑上式的中间项，由于这是一个标量，利用“迹算子”进行计算数值不改变:

注意到在线性回归中，普通最小二乘估计下的样本残差与解释变量是正交的，即对所有的j有:

因此也有:

这样就有:

因为Ω是正定矩阵，它的逆矩阵Ω-1也是正定矩阵。因此，定义一个n×1维向量:

则上式最后一项可以表示成为:

因此，上式达到最小值时要求: x*t=0，即Π=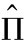，这意味着OLS回归估计为向量自回归系数提供了极大似然估计。

(3)Ω的极大似然估计。

我们可以利用矩阵导数的一些公式来获得Ω的极大似然估计。在Π的极大似然估计处，条件似然函数为:

我们的目的是选择对称正定矩阵使得上述函数达到最大。类似的矩阵导数运算得到:

上述矩阵的第i行和第j列元素的估计为:

这里残差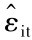是VAR模型中第i个变量基于常数和所有变量的p阶滞后进行回归普通最小二乘估计得到的残差。

(4)向量自回归模型的似然比检验(Likelihood Ratios Tests)。

为了实施似然比检验，我们需要计算极大似然函数的具体数值，为此，我们考虑:

上式中的最后一项是:

代入到似然函数中，得到:

这使得似然比检验比较容易进行。假设我们希望检验的原假设是一组变量是由具有p0阶滞后变量的高斯VAR模型产生，而备选假设是滞后变量阶数为p1＞p0。为了在原假设下估计系统，我们对系统中的每一个变量基于常数和所有其他变量及其p0阶滞后变量进行最小二乘回归，设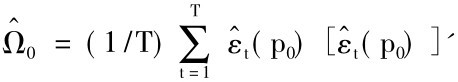是从这些回归中得到的残差的方差—协方差矩阵。因此在原假设H0下对数似然估计的极大值是:

类似，该模型系统可以利用最小二乘估计对包括所有变量p1阶滞后变量进行线性估计，得到备选假设下对数似然函数的最大值是:

这里是从第二组变量集合中获得的方差—协方差矩阵。则似然比对数的两倍可以表示为:

在原假设下，似然比统计量具有χ2—分布的渐近分布，自由度是附加在原假设H0上约束的数目，系统中每个方程在原假设H0上的约束条件是每个变量减少了(p1-p0)个滞后变量，因此一个方程中的参数零约束是n(p1-p0)，因此整个VAR模型系统的约束条件数目n2(p1-p0)，因此上述似然比统计量在原假设成立时的渐近分布是χ2［n2(p1-p0)］。

例如，假设在滞后3阶和4阶的情形下估计一个二元VAR模型，这时的参数阶数为: n=2，p0=3，p1=4，假设原始样本中每个变量包含50个观测值，表示为y-3，y-2，…，y46，观测值1至46用于估计滞后3阶和4阶指定时的系统参数，因此这时T=46。假设(p0)表示t时yit基于常数、y1t的3阶滞后和y2t的3阶滞后进行回归的残差，假设计算得到:

则有:

计算这个矩阵的对数行列式值为: 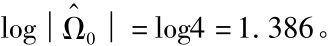类似地，假设将变量的滞后4阶变量加入到回归方程中来，则可以得到残差的协方差矩阵为:

这个矩阵的对数行列式值为: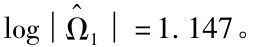则有:

2(L*1-L*0)=46(1.386-1.147)=10.99

检验统计量的自由度为22(4-3)=4，由于10.99＞χ20.05(4)=9.49，因此拒绝原假设，认为模型的动态性没有被VAR(3)描述，这时采用VAR(4)更为合适。

Sims(1980)提出了一种修正的似然比检验，该检验考虑了小样本带来的偏差。他建议的统计量为:

这里的k是每个方程中需要估计的参数个数。这个修正后的统计量保持原来的渐近分布，但是降低了小样本情形下拒绝原假设的可能性。对上面的例子而言，检验统计量为:(46-9)(1.386-1.147) =8.84

此时，我们将得到相反的检验结果，而原假设是被接受的。

2. 二元Granger因果关系检验(Bivariate Granger Cau-sality Tests)

一个能够利用VAR模型处理的关键问题是如何描述一些变量预测其他变量时的有用程度。下面我们主要分析由Granger(1969)提出的，由Sims(1972)推广的预测两个变量之间关系的方法。

(1)二元Granger因果关系的定义(Definition of Bivariate Granger Causality)。

我们在这里分析的主要问题是一个标量随机变量y对于预测另外一个标量随机变量x是否有帮助? 如果没有任何帮助，则称变量y没有Granger影响变量x。更为正式地，如果对所有s＞0，xt+s基于(xt，xt-1，…) 进行预测的均方误差(MSE) 与 xt+s基于(xt，xt-1，…)和(yt，yt-1，…)进行预测的均方误差是一样的，则称变量y无法Granger影响变量x(y fails to Granger-cause x)。

如果我们将预测限于线性预测，则当:

则称变量y无法Granger影响变量x。

等价地，如果上述预测无助性成立，那么这时我们也称“变量x在时间序列意义上相对于变量y是外生的(x is exogenous in the time series sense with respect to y)。

与上述意义相同的第三种表示是: 如果上述预测无助性成立，则称y关于将来的x是非线性信息化的(y is not linearly informative about future x)。

提出如此定义的Granger观点是: 如果一个事件Y是另一个事件X的原因，则事件Y应该发生在事件X之前。但是，即使人们从哲学角度同意这样的观点，但在使用累积时间序列数据来实现这样的观点上遇到了巨大的障碍。为此，我们首先需要考虑二元系统中表示Granger因果关系的时间序列表示的机理。

(2)Granger因果关系的另外一种启示(Alternative Implications of Granger Causality)。

在描述x和y的二元VAR模型中，如果对所有j，下述模型中的系数矩阵Φj是下三角矩阵，则称变量y无法Granger影响变量x。

从这个模型系统的第一行可知，变量x的一阶段向前预测仅依赖自身的滞后值，不依赖变量y的任何滞后值:

进一步，从模型中可以获得xt+2的值为:

根据投影的迭代法则，以t时刻的(xt，xt-1，…; yt，yt-1，…)为基础的预测也仅仅依赖(xt，xt-1，…，xt-p+1)。通过归纳，上述推断对任何s步长的预测都是成立的，因此上述断言成立: 如果对所有j，上述模型中的系数矩阵Φj是下三角矩阵，则变量y无法Granger影响变量x。

根据向量回归方程中的结论，我们有下面的公式成立:

Ψs=Φ1Ψs-1+Φ2Ψs-2+…+ΦpΨs-p，s=1，2，…

这里Ψ0是单位矩阵，Ψs=0，s＜0。这个表示意味着，如果对所有j，矩阵Φj是下三角矩阵，则对所有的s，基础表示中的移动平均矩阵Ψs也是下三角矩阵。因此，如果变量y无法Granger影响变量x，则MA(∞)过程的表示为:

这里:

Sims(1972)给出了Granger影响关系的另一种启示。这样的启示可以从下面的命题得到。

命题11.1 考虑变量yt依赖过去、当前和将来xt的线性投影:

这里系数bj和dj定义为母体投影系数，即对所有的t和τ，有:

E(ηtxτ) =0

则“变量y非Granger影响变量x”的充分必要条件是:

dj=0，j=1，2，…

(3)Granger因果关系的计量检验(Econometric Tests for Granger Causality)。

计量检验两个具体的可以观测到变量之间是否具有“变量y非Granger影响变量x”的关系，都可以在上面论述的三种Granger影响关系的意义上进行。最简单也可能是最好的方法是使用自回归方程中的下三角指定。为了进行这样的检验，我们假设一个特殊的滞后阶数为p的自回归方程并利用OLS估计下面的方程:

xt=c1+α1xt-1+α2xt-2+…+αpxt-p+β1yt-1+β2yt-2+…+βpyt-p+ut(www.daowen.com)

我们然后对下述原假设进行F—检验:

H0: β1=β2=…=βp=0

根据前面的命题8.2，实施检验的一种方法是计算上述回归的残差平方和:

将这个平方和与仅依赖xt进行回归的残差平方和进行比较:

这里的单变量回归方程是:

xt=c0+γ1xt-1+γ2xt-2+…+γpxt-p+et

定义F—统计量为:

如果该统计量大于F(p，T-2p-1)分布的5%临界值，则我们拒绝“变量y非Granger影响变量x”的原假设。这就是说，当S1充分大的时候，我们能够得到“变量y确实Granger影响变量x”的结论。

在对于具有固定回归因子和高斯扰动时，上述检验统计量在原假设成立时具有精确的F—分布，然而，如果在Granger因果回归中具有滞后相依变量的话，那么上述检验只是渐近的。渐近的等价检验统计量为:

如果S2大于χ2(p)分布的5%临界值，则拒绝原假设“变量y非Granger影响变量x”。

另一种方法是利用基于Sims形式的检验来代替基于Granger形式的检验。与Sims形式有关的一个问题是，其中的误差项在一般情况下是自相关的。因此检验“dj=0，j=1，2，…”的标准F—检验无法给出正确的答案。解决这种问题的一种方法是可能存在自相关性的误差项进行变换，假设误差项ηt具有Wold表示: ηt=ψ22 (L)v2t，在模型两端乘以逆算子: h(L)≡［ψ22(L)］-1，得到:

这时，上述模型中的误差项v2t是白噪声过程，并且与其他解释变量无关。进一步，这时也有: “对任意j，dj=0”的充分必要条件是“对任意j，d*j=0”。因此，对上述模型中的无限求和在某个整数q上截断，就可以利用检验“d*1=d*2=…=d*q=0”的F—统计量来检验原假设“变量y非Granger影响变量x”。

在Granger影响关系的经验检验中，人们发现检验结果对选取的滞后阶数q是比较敏感的，同时，检验结果也依赖处理可能数据存在非平稳性的方法。这些都是在使用Granger影响关系检验中应该注意的问题。

(4)解释Granger因果关系检验(Interpreting Granger-Causality Tests)。

“Granger因果关系”与因果关系的标准含义是如何产生关系的? 我们通过几个例子来说明这个问题。

①Granger因果关系检验和前瞻行为。

我们继续考虑股票投资者的例子。假设在时刻t，一个投资者以价格Pt购买一股股票，则在时刻t+1，投资者可以获得红利Dt+1，并以价格Pt+1出售这股股票。这种股票的事前收益率(Expost Rate of Return，表示为rt+1)可以按照下式定义:

(1+rt+1)Pt≡Pt+1+Dt+1

如果在所有时刻股票的预期收益率是常数r，则下列一个简单的股票价格模型成立:

(1+rt)Pt=Et［Pt+1+Dt+1］

这里Et表示股票市场参与者利用时刻t能够获得的所有信息做出的期望。在上述公式中包含的逻辑关系是，如果投资者在时刻t获得的信息促使他们推测股票将具有高于正常的收益率，则他们将在时刻t购买更多的股票。这样的购买将促使股票价格Pt上升，直到上述公式得到满足。这样的观点有时被称为有效市场假说。

如果满足有界性条件，则股票价格路径满足:

因此，按照有效市场假说，股票价格中包含将来所有红利现值的最优预测。如果这个预测是基于多余所有过去红利的信息基础上的，因为投资者企图推断红利中的变动，则股票价格将对红利产生Granger影响。

为了比较简单地解释这一点，我们假设:

Dt=d+ut+δut-1+vt

这里和ut和vt是独立的高斯白噪声序列，d是均值红利。假设投资者在时刻t知道所有的{ut，ut-1，…}和{vt，vt-1，…}。则基于这些信息对红利Dt+j的预测是:

将这些预测值代入到股票价格的贴现公式，得到:

因此，对这个例子而言，股票价格是白噪声，因此无法在滞后股票价格或者红利的基础上进行预测。没有序列能够对股票价格产生Granger影响。

另外，注意到公式中的ut-1能够从滞后股票价格中恢复出来。

上式说明，ut-1中具有除了包含在{Dt-1，Dt-2，…}以外的有关Dt的信息。因此，股票价格对红利具有Granger影响，虽然红利对股票价格没有Granger影响。因此，二元VAR模型具有下述形式:

因此，在这个模型中，Granger影响关系体现的因果关系是按照相反方向起作用的。红利没有对价格产生Granger影响，即使投资者对红利的察觉是股票价格的唯一确定成分。另外，价格确实对红利产生了Granger影响，虽然现实中股票的市场估价对红利过程没有任何影响。

一般地，如股票和利率等反映前瞻性行为的时间序列经常被认为可以作为许多关键时间序列非常优秀的预测因子。显然这并不意味着这些时间序列促使GDP或者通货膨胀率上升或者下降。取而代之的是，这些时间序列的数值反映了GNP或者通货膨胀率的走势市场最优信息。对于评价有效市场观点，或者研究市场是否考虑或者能够预测GDP或通货膨胀率等，对这些序列的Granger影响关系检验时有帮助的，但不应该用于推断因果性的方向。

从来就没有那样的情景，Granger因果关系用来为真实因果关系的方向提供有帮助的迹象。作为这种论题的示意，可以考虑试图度量石油价格上涨对经济的作用结果。

②检验强经济计量外生性(Testing for Strict Econometric Exoge-neity)。

第二次世界大战以后，美国经济中偶然出现的经济衰退之前，经常伴随着原油价格的急剧上升，这意味着石油价格冲击是经济衰退的原因吗?

一种可能性是这种相关性是一种巧合，石油冲击和经济衰退只是偶然地在近似的时间内发生，而产生这两个时间序列的真实机制是不相关的。我们可以通过检验石油价格没有Granger影响到GNP这样的零假设来判断这样的假设。这样的假设被实际数据的检验所拒绝，即结论是石油价格有助于推断GNP的取值，它们对推断的作用是显著的。这样的讨论反对相关性是一种偶然的论点。

为了对这种关系给出一种解释，我们需要确定石油价格中的上升并没有反映出那些确实是导致衰退的其他宏观经济影响。石油价格上升的主要原因出于一些十分清楚的历史事件的影响，例如，1956—1957年的Suez危机，1973—1974年的Arab-Israeli战争等，人们可以接受这样的观点，即这些事件的形成原因完全属于美国经济以外的，而且是完全不可预测的。如果这个观点是正确的，则石油价格与经济衰退之间的历史相关性可以被解释为一种因果影响关系。这样的观点还具有一个可以辩论的支持，即没有时间序列能够Granger影响到石油价格序列。从经验上看，人们确实很少发现一些宏观时间序列能够有助于推断石油危机发生的时点。

这两个例子的主题是Granger因果关系检验能够作为检验关于特定时间序列可推断性的假设的有效工具。另外，人们可能会怀疑他们作为建立任意两个时间序列之间影响关系方向的一般诊断机制的功效。出于这个原因，最好将这个检验描述为检验是否y有助于预测x，而不是检验是否y影响x。这样的检验对后一个问题有一定的启发，但只有附加其他假设才具有意义。

到目前为止，我们只考虑了两个变量x和y，将它们与其他变量分离开来。假设还有其他变量与x或者y产生交互影响，这会对预测x和y之间的关系产生什么样的影响呢?

③缺损信息的作用(Role of Omitted Information)。

考虑下面三个变量构成的模型系统:

假设残差向量满足:

因此，上述模型表示y3在预测y1或者y2的过程中，比仅仅使用y1和y2滞后值相比没有任何改进。

我们现在考虑检验变量y1和y3之间的Granger影响关系，首先考虑关于y1的过程:

y1t=ε1t+δε1t-1+ε2t-1

注意到过程y1是一个一阶移动平均过程{ε1t+δε1t-1}与一个不相关的白噪声过程 ε{2t-1}之和。我们已经证明了这样的过程仍然是一个一元MA(1)过程，具有类似表示为:

y1t=ut+θut-1

根据第四章的结论，可以知道预测误差可以表示为:

ut=(ε1t-θε1t-1+θ2ε1t-2-θ3ε1t-3+…)+δ(ε1t-1-θε1t-2+θ2ε1t-3-θ3ε1t-4+…)+(ε2t-1-θε2t-2+θ2ε2t-3-θ3ε2t-4+…)

当然，一元预测误差ut与自身滞后值是无关的。但是，需要注意到它与y3，t-1相关:

E［(ut)(y3t-1)］=E［(ut)(ε3t-1+ε2t-2)］=-θσ22

因此，滞后的y3可以有助于改进y1的预测，而它原来是仅仅基于y1滞后值进行预测的。这意味着在二元系统中y3能够Granger影响y1。其原因是y3的滞后值与省略变量y2是相关的，这个省略的变量对预测y1也是有帮助的。

3. 限制性向量自回归模型的极大似然估计(Maximum Likelihood Estimation of Restricted Vector Autoregressions)

在第一节中我们讨论了无限制向量自回归模型的极大似然估计和假设检验问题。在这个VAR模型中每个方程都具有相同的解释变量，即常数加上系统中所有变量的滞后变量。我们已经说明了如何计算线性约束的Wald检验，但我们没有讨论系统具有约束条件时的参数估计问题。因此，这节中我们考虑限制性VAR模型的估计问题。

(1)多元情形下的Granger因果关系(Granger-Causality in a Mul-tivariate Context)。

作为一个我们在估计中感兴趣的限制性系统的例子，考虑前面已经讨论过问题在向量情形下的推广。考虑VAR模型中的变量可以分成两个群体，利用n1×1维向量y1t和n2×1维向量y2t表示。这时VAR模型可以表示为:

这里x1t是包含y1t滞后值的(n1p×1)向量，x1t是包含y1t滞后值的(n1p×1)向量:

模型中n1×1维向量c1和n2×1维向量c2表示包含VAR模型中的常数项。而矩阵A1，A2，B1，B2包含自回归系数。

如果包含在y2中的元素对于预测包含在y1中的任意元素没有任何帮助，则这种预测是仅仅依赖y1中所有元素的滞后值的。这时，我们称在时间序列的意义上，由变量y1的一组变量相对于y2中的变量是块外生的(Block-exogenous)。在上述模型系统中，当矩阵A2=0时，y1是块外生的。为了讨论受到这个约束限制的系统，我们首先关注非限制性极大似然估计计算和估计的另外一种形式。

(2)极大似然函数的另外一种表示(An Alternative Expression for the Likelihood Function)。

我们在第一节中使用推断误差分解计算了VAR模型的对数似然函数:

这里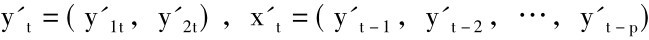，函数形式为:

另外，上述联合概率密度也可以表示成为y1t的边际分布密度与给定y1t条件下y2t的条件概率分布密度的乘积:

基于条件xt，y1t的条件概率密度为:

而给定y1t和xt时y2t的条件概率密度也是正态的:

这个条件分布密度中的参数可以利用下面的公式求得，其中，条件方差为:

而条件均值为:

注意到从方程中可以获得:

将这些表达式代入到条件均值中:

这里:

因此，联合概率密度的对数似然函数可以表示为边际密度对数和条件密度对数之和，表示为:

其中:

这样一来，样本对数似然函数可以表示为:

注意到上面我们获得了似然函数的两种表达式，只要它们的参数矩阵之间具有上述之间的转换，那么两种似然函数的计算将得到同样的数值。如果一个似然函数通过选择参数向量(c1，A1，A2， c2，B1，B2，Ω11，Ω12，Ω22)来极大化，那么同样的似然函数值可以通过选择参数向量(c1，A1，A2，c2，B1，B2，D0，D1，D2， Ω11，H)来极大化另一个似然函数达到。

其中，第二部分的似然函数的极大化很容易获得。

4. 冲击反应函数(The Impulse-Response Function)

按照前面的论述，VAR模型可以表示为向量MA(∞)形式:

yt=μ+εt+ψ1εt-1+ψ2εt-2+…

因此，矩阵ψs可以解释为:

表示成为分量形式为:

这是假设在所有时刻其他扰动保持不变，时刻t出现在第j个变量扰动(εjt)的一个单位增加对t+s时刻第i个变量(yi，t+s)的影响结果。

如果在相同时刻εt的第一个元素改变δ1，第二个元素改变δ2，第n个元素改变δn，则这些改变对yt+s的综合作用效果为:

ψs的第i行和第j列元素(ψs)ij=［∂ yi，t+s］/［∂ εj，t］作为时间间隔s的函数，我们称此函数为脉冲响应函数(Impulse Response Function)。

VAR模型分析的作用。向量自回归VAR模型主要作用在于三个方面: 首先是估计解释变量的回归参数的，以及有关的检验统计量; 其次是分解解释变量的方差，它解释了在每一个解释变量的方差中，其他解释变量所占的解释比例或者份额; 最后是脉冲响应函数(Impulse Response Function)的含义，脉冲响应函数解释了变量是如何在各期对各种冲击作出不同的反应。比如，在采用向量自回归VAR模型估计通货膨胀，可以估计的货币因素的参数的显著程度;此外，通过对方差进行分解，还可以分析货币政策变动对通货膨胀变动时的影响程度，例如，货币政策的变动对通货膨胀率的变动的影响程度是70%，说明对比于其他所有影响通货膨胀的因素当中，货币政策是非常重要的因素; 然后通过脉冲反应函数的分析，能够反映通货膨胀对于货币政策变动的响应程度。但是，构建方差分解和脉冲响应函数之前，VAR模型中的解释变量必须以一定的次序进行排列(Sims，1980)，因为从理论上的分析是根据被解释变量的重要程度来进行排列的。

采用向量自回归模型展开分析前，首先需要检验变量之间的因果关系，通常会采用格兰杰Granger因果检验。Granger检验虽然是重要的因果关系分析工具，但并不是唯一和最优的方法，主要原因在于: ①Granger检验从其检验思想和检验形式的本质来说是从“有助于预测”的角度说明从某一变量到另一变量的因果流的存在性，如我们不能从Granger检验的结果推断一个变量变动导致另一变量变动的方向; ②因果检验不能说明变量间相互影响的强度和整个动态过程，而我们所真正关心的研究问题中，谁是因、谁是果，还包括某一变量变动导致另一变量变动的方向如何、相互影响的强度怎样、随时间有何变化、变量之间相互关系发生了什么变化等一系列细节问题。这些问题的答案是可以通过脉冲响应函数和方差分解来反映的。

向量自回归VAR方法也存在一些不足之处，但与结构性的经济计量模型存在不同。向量自回归VAR模型并不能解释货币政策变化是如何影响资产价格变动的传导机制，因此，不能说明产生这种结果的原因。例如，有学者利用VAR模型对美国的数据进行了估计，表明债券的流通数量能够领先物价水平，也就是说，债券的流通数量能够预测物价的未来趋势。然而，从理论上分析，由于债券的数量的变动仅仅是对需求发生变化的反映，很难解释为什么债券的需求对物价的变化能起到领先影响的作用。存在的可能原因很多，可能是由于公众对债券的需求提高了大家对未来价格上涨的预期。这种解释只能强调债券流通的重要性，也只是可以判断未来价格趋势的一个指标，但不能认为债券的流通是影响未来价格上涨的原因。这是因为，向量自回归方法的设立并不要求基于扎实的经济理论假定。在研究样本的期间内，某实体的经济行为模式发生变化后，向量自回归经济模型也会失效，导致向量自回归得出的结果也会产生误差。

综上所述，本书结合资源能力理论和双边市场理论的理论模型基础，并综合向量自回归模型来克服以上的问题，令结论更具有说服力。