再制造升级周期环境影响评价需要从人体健康、生态环境、资源使用等方面对再制造升级做一个综合评判，因此是一个多指标评价过程。常用的多指标评价方法有层次分析法（AHP）、综合指数法、模糊综合评判法和灰色聚类法等。由图6-5可以看出，再制造升级周期环境评价指标体系是一个递阶层次结构，因此利用AHP能够很好地实现再制造升级周期环境影响评价。AHP是一种实用的多准则决策方法，这种分析方法把一个复杂问题表示为有序的递阶层次结构，通过人们的判断对决策方案的优劣进行排序。它能将决策中的定性和定量因素进行统一处理，具有简洁和系统等优点，很适合在复杂系统中使用。

再制造升级周期环境影响评价在针对其指标体系进行评价时，需要从指标体系中的C层（气候变暖、臭氧耗竭、…）开始逐层向上合并，直到最终得到一个总环境影响指数（A层）。整个评价过程就需要利用AHP来实现指标合并过程，确定同一层几个不同指标相对上一层与之关联的某一指标的权重分配。下面为按照AHP的步骤进行指标逐层合并以及权重分配^［6］。

1.构造递阶层次结构模型 AHP的递阶层次结构一般包括目标层、指标层、方案层等，在再制造升级周期系统的递阶层次结构模型，即图6-6所示的评价指标层次体系中，目标层为总环境影响指数，B层到D层为指标层，E层为方案层。

2.构造相对重要度判断矩阵

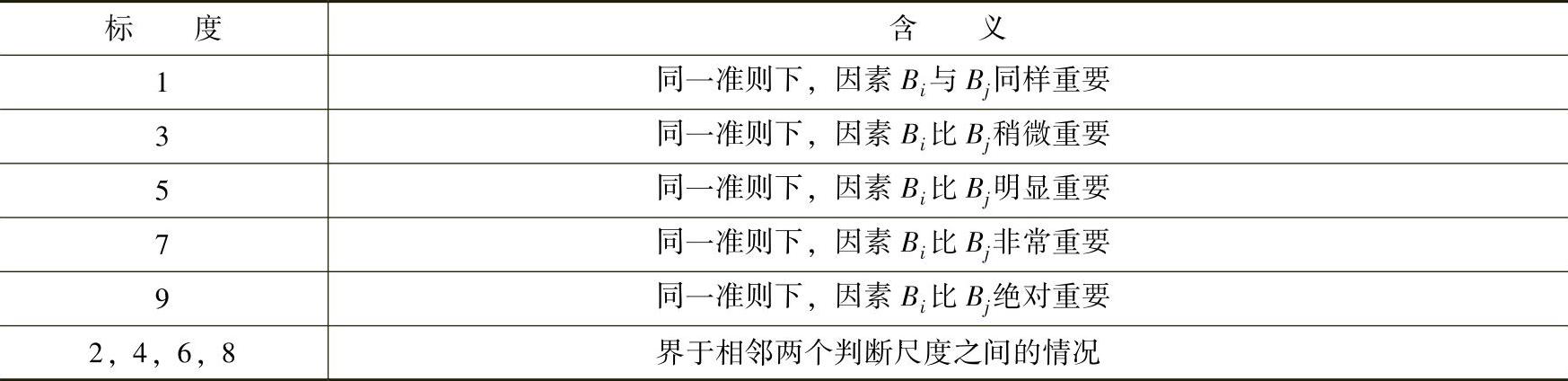
在建立层次模型后，上下层次之间的元素隶属关系就已经确定下来了。对上一层的某个指标来讲，下一层与之关联的几个指标在向其合并的过程中，应当进行权重的分配。要确定权重，首先要构造相对重要度判断矩阵，以此来确定各因素之间的相对重要程度。AHP是通过因素间的两两对比来描述因素之间相对重要程度的，即每次比较只有两个因素，而衡量相对重要程度的差别是使用1～9比率标度法，具体含义见表6-8。

表6-8 相对重要度的1～9比例标度值

通过上述的两两比较，就可得到进一步计算必需的判断矩阵。具体地说，假设A层因素Ak与下一层即B层的因素B₁，B₂，…，Bn有联系，判断矩阵见表6-9。

表6-9 判断矩阵

评价方法采用上述形式构造了再制造升级周期环境影响评价指标体系的各相对重要度判断矩阵。

1）B层相对重要度判断矩阵见表6-10。

表6-10 总环境影响指数下层相关指标的相对重要度判断矩阵

2）C层相对重要度判断矩阵见表6-11～表6-13。

表6-11 人体健康下层相关指标的相对重要度判断矩阵

表6-12 生态环境下层相关指标的相对重要度判断矩阵

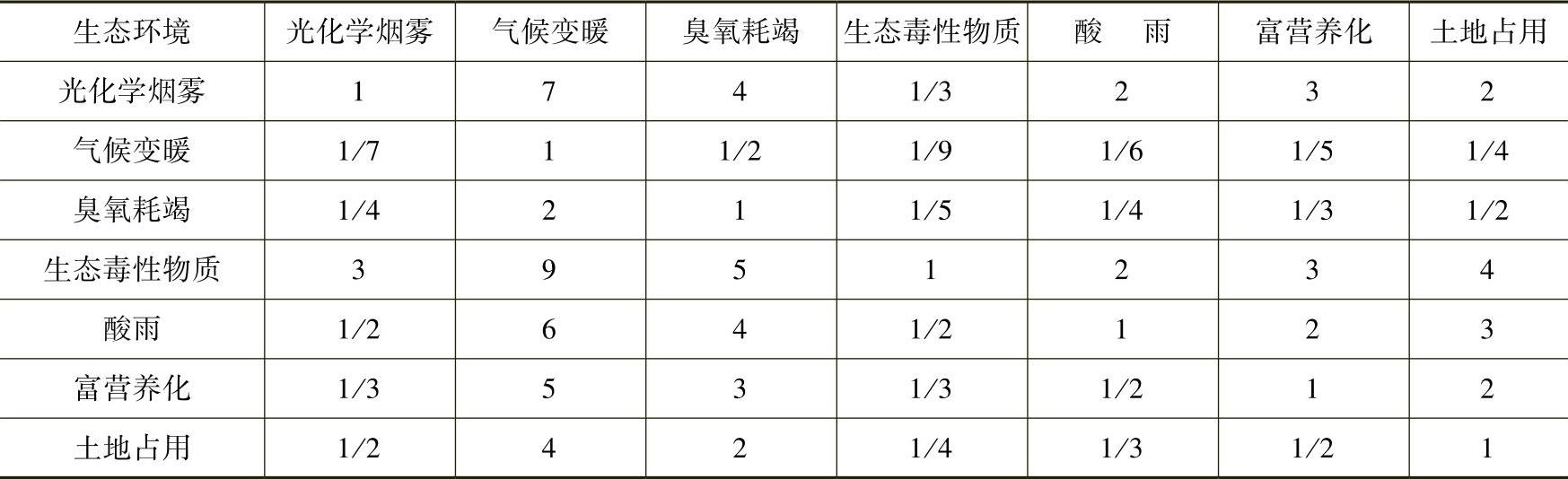
表6-13 资源使用下层相关指标的相对重要度判断矩阵

3.确定权重

相对重要性判断矩阵实质上是将关于各因素重要程度差别的信息分散在矩阵的n×n＝n²个元素中。要将这些信息提取出来，以权重的方式给出，AHP采用的是特征向量法。

首先计算出判断矩阵的特征向量，通过求解下面的方程可以得到特征向量P

AP＝λ_max P（6-21）

式中 A———相对重要性判断矩阵；

λ_max———矩阵A的最大特征值。(www.daowen.com)

可以利用式（6-22）求特征向量P的分量P_i

式中b_ij———矩阵A中的元素。

然后对特征向量P进行归一化，从而得到权重向量w。归一化的过程为首先得到

然后可以求得权重向量w的各分量

利用以上方法可以分别求得表6-10～表6-11四个判断矩阵的权重向量，见表6-14。

表6-14 再制造升级周期环境影响评价的权重向量

4.一致性检验

在构造相对重要度判断矩阵时，评价者往往不可能精确确定各指标之间的相对重要性，因此判断矩阵通常都具有偏差。虽然并不要求判断矩阵具有一致性，但如果偏差过大时，利用AHP求得的权重将会出现某些问题。因此需要进行一致性检验，这是保证结论可靠的必要条件。

首先要求出判断矩阵的最大特征值λ_max，可采用式（6-25）求得

然后计算一致性指标CI

其中n为判断矩阵的阶数。接下来计算相对一致性指标CR

RI为平均随机一致性指标，是足够多个根据随机发生的判断矩阵计算的一致性指标的平均值。1～10阶矩阵的RI取值见表6-15。

表6-15 1～10阶矩阵的RI取值

一般而言，CR越小，判断矩阵的一致性越好，通常认为CR≤0.1时，判断矩阵具有满意的一致性。

按照上述步骤，可以对再制造升级周期环境影响评价体系的权重分配进行一致性检验，见表6-16。

表6-16 再制造升级周期环境影响评价体系权重分配一致性检验

从表中可以看出，各CR均小于0.1，也就是说四个判断矩阵均具有满意的一致性。