以本节开始介绍的实例为背景。A某天早上接到10个配送任务，分别用1，2，…，10表示每个任务，也称需求点。其中，需求点3和8是企业的重点客户，他们的配送任务必须由A完成。用0表示配送中心，A必须从配送中心出发执行配送任务，并最终回到配送中心。表10-2为配送中心、各需求点之间的公路距离。假设车辆的行驶速度为50km/h，则配送中心、各需求点之间的时间距离可以利用公路距离除以车辆行驶速度计算出来，如表10-3所示。表10-4是各需求点所需的服务时间、时间窗要求及A可获得的收益。表10-5为各需求点的时间窗甘特图，从中可以直观地看到每个需求点的时间窗。其中行代表需求点的编号，列代表时刻，每行的直线代表相应需求点的时间窗跨度。图10-2为配送中心、各需求点的相对位置图及相关参数。其中小实心矩形代表配送中心，五角星代表指定点，即必须为其服务的需求点，圆心代表除指定点外的其他需求点。配送中心及各需求点的编号、时间窗、服务时间均标识在代表图形的附近。

表10-2 配送中心及各需求点之间的公路距离（单位：km）

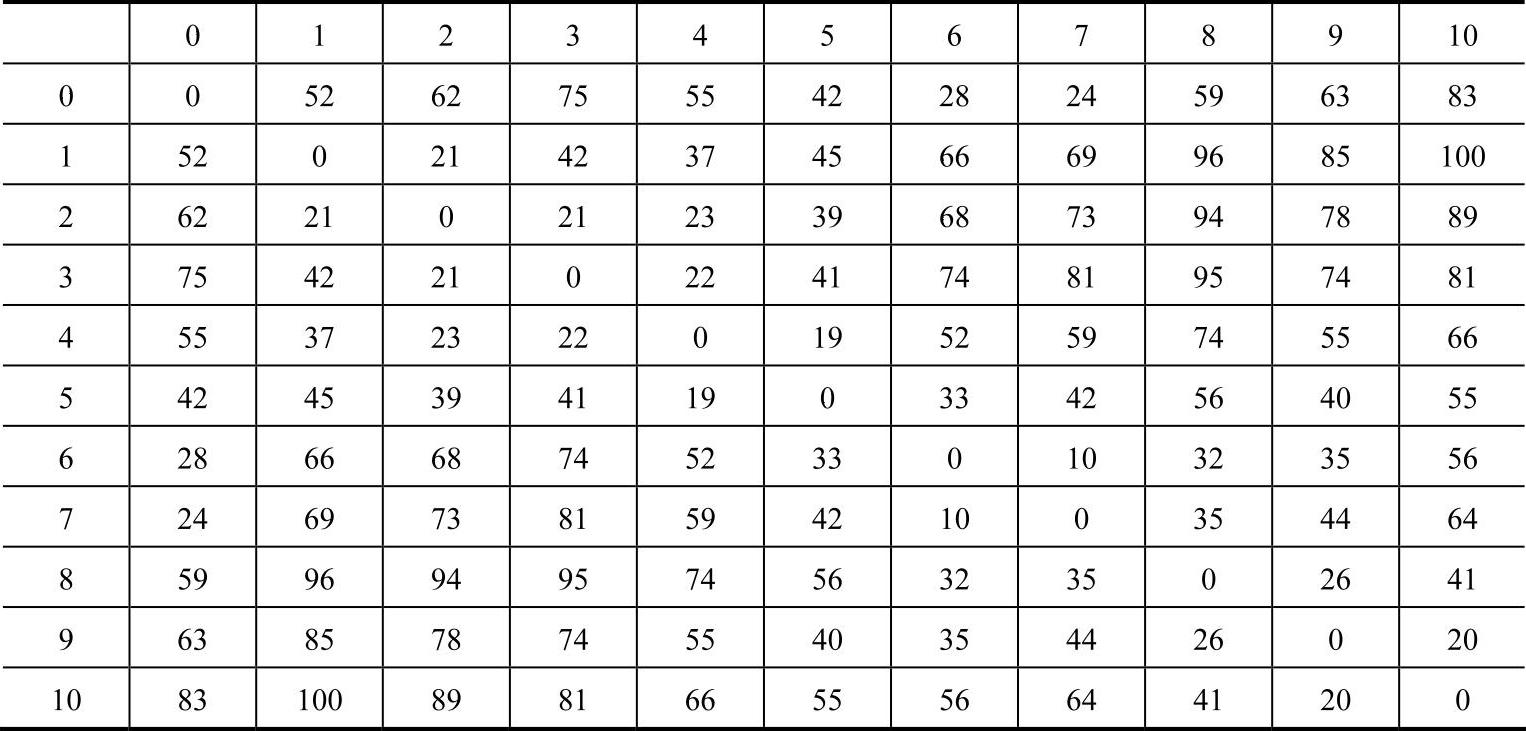
表10-3 配送中心及各需求点之间的时间距离 （单位：h）

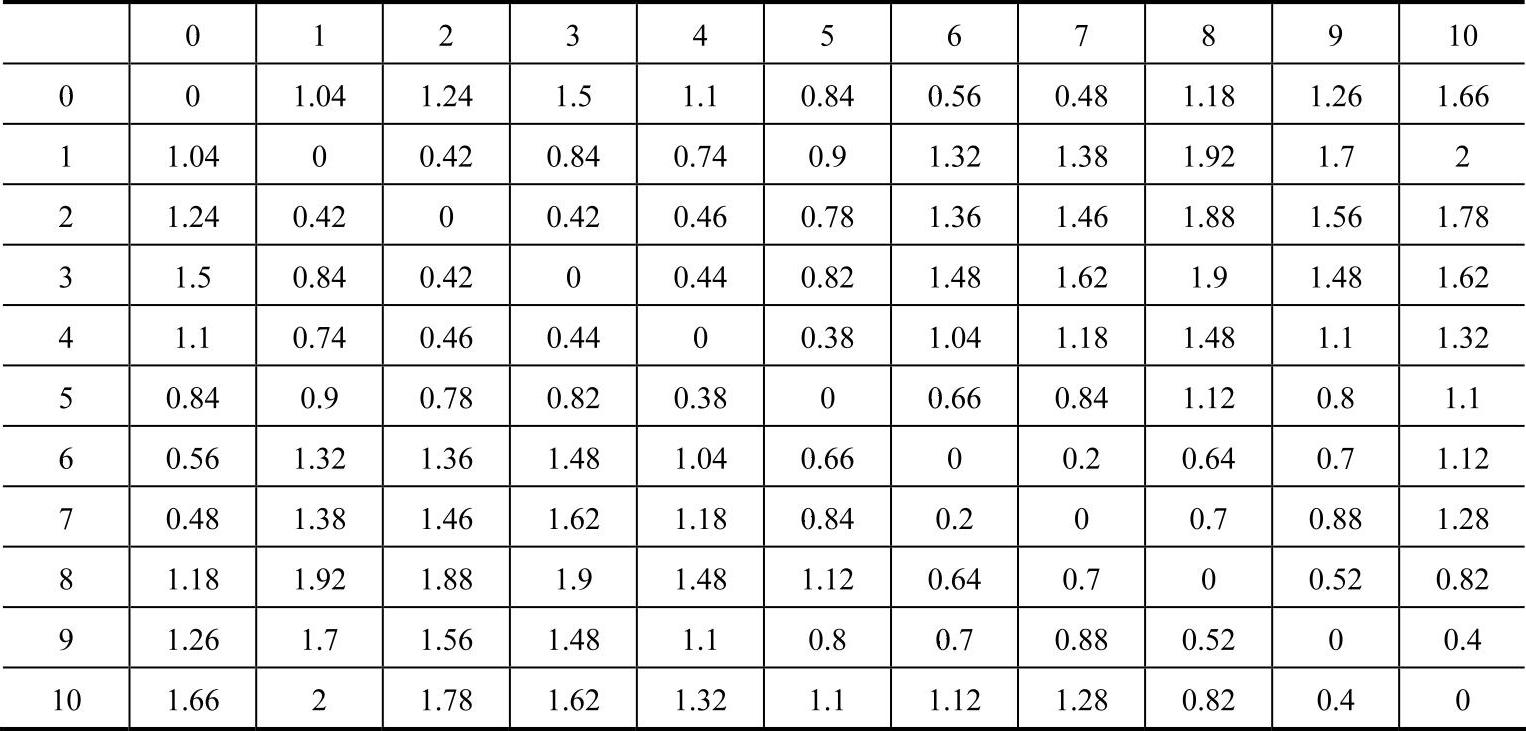
表10-4 每个需求点的需求量、服务时间、配送时间窗及收益

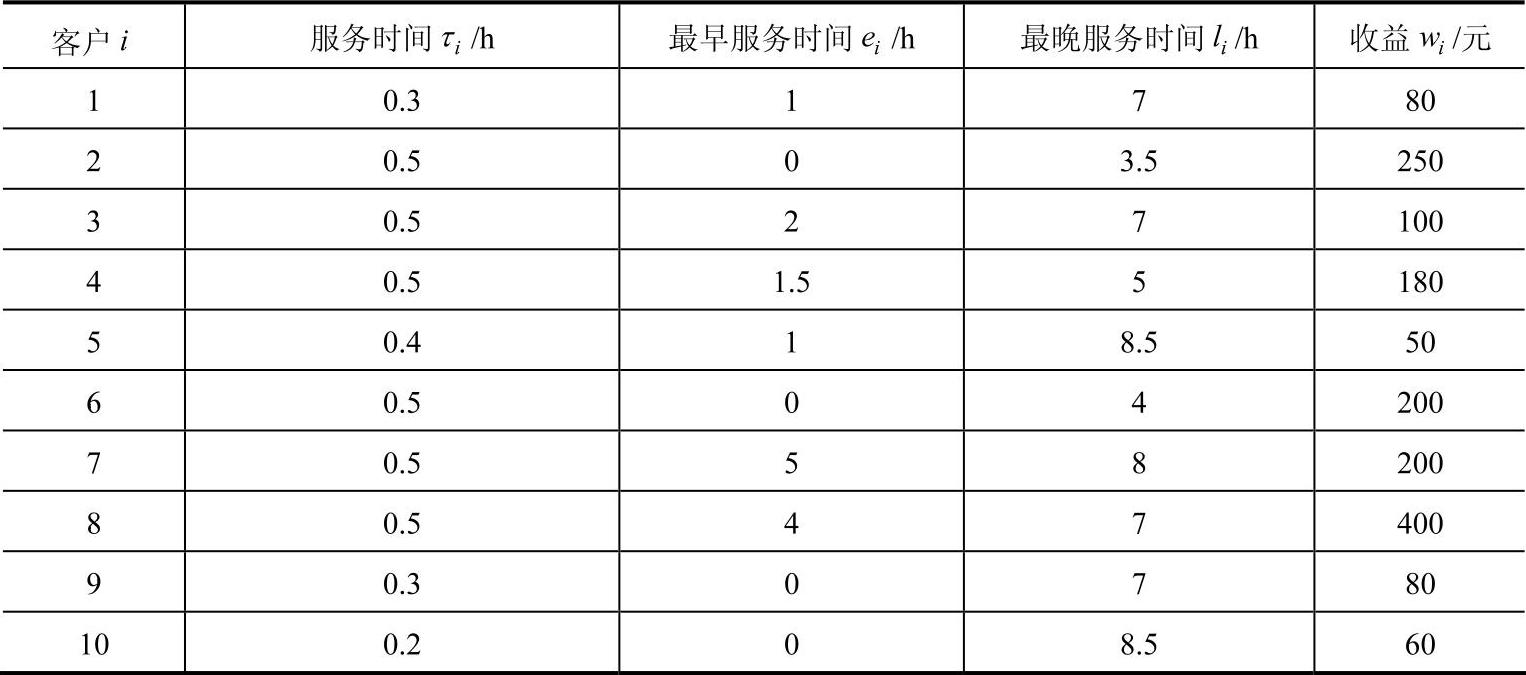
表10-5 各需求点时间窗的甘特图

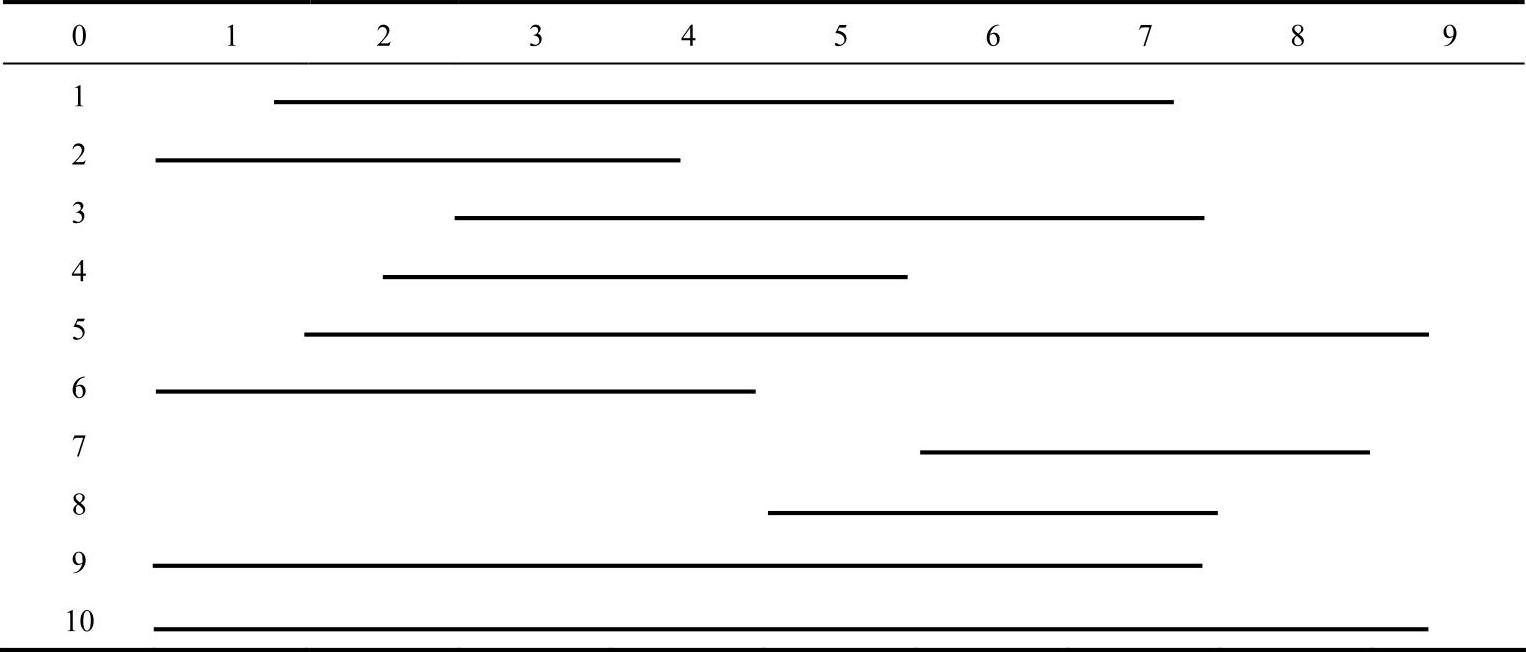
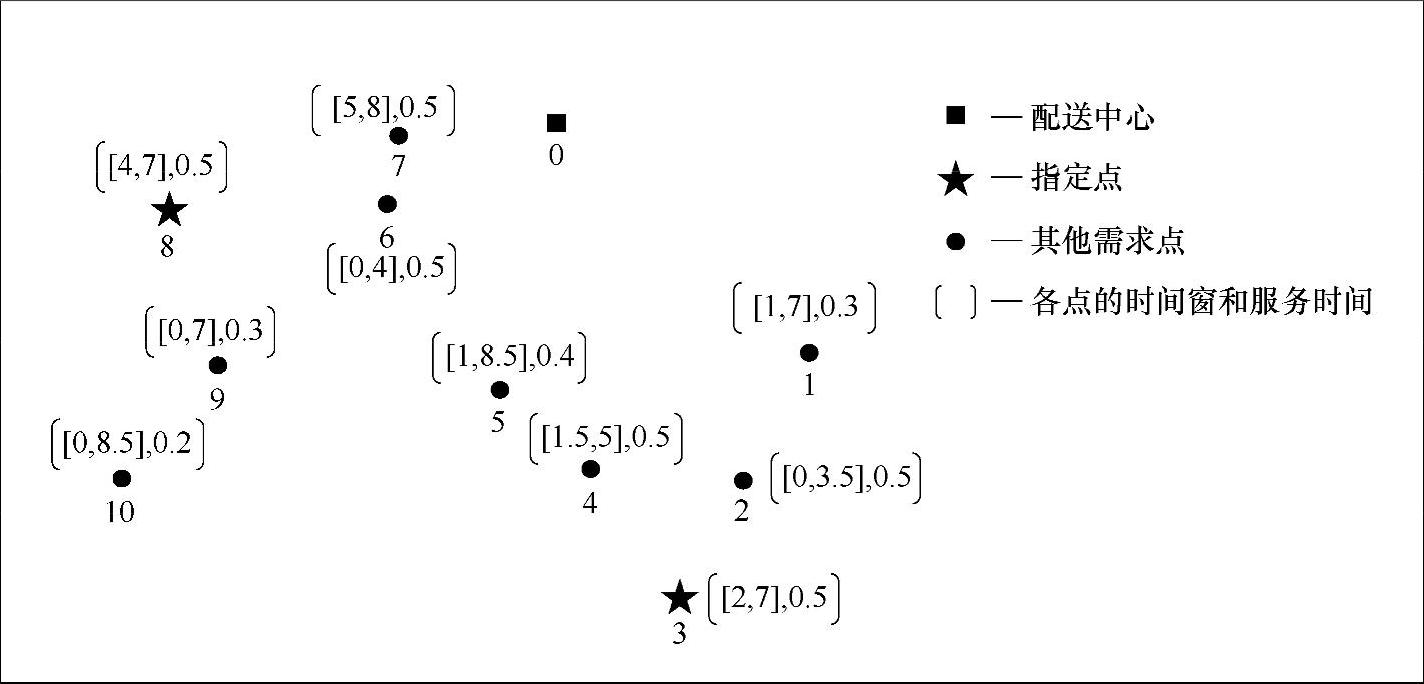
图10-2 配送中心及各需求点的相对位置图及相关参数

1.精确算法求解

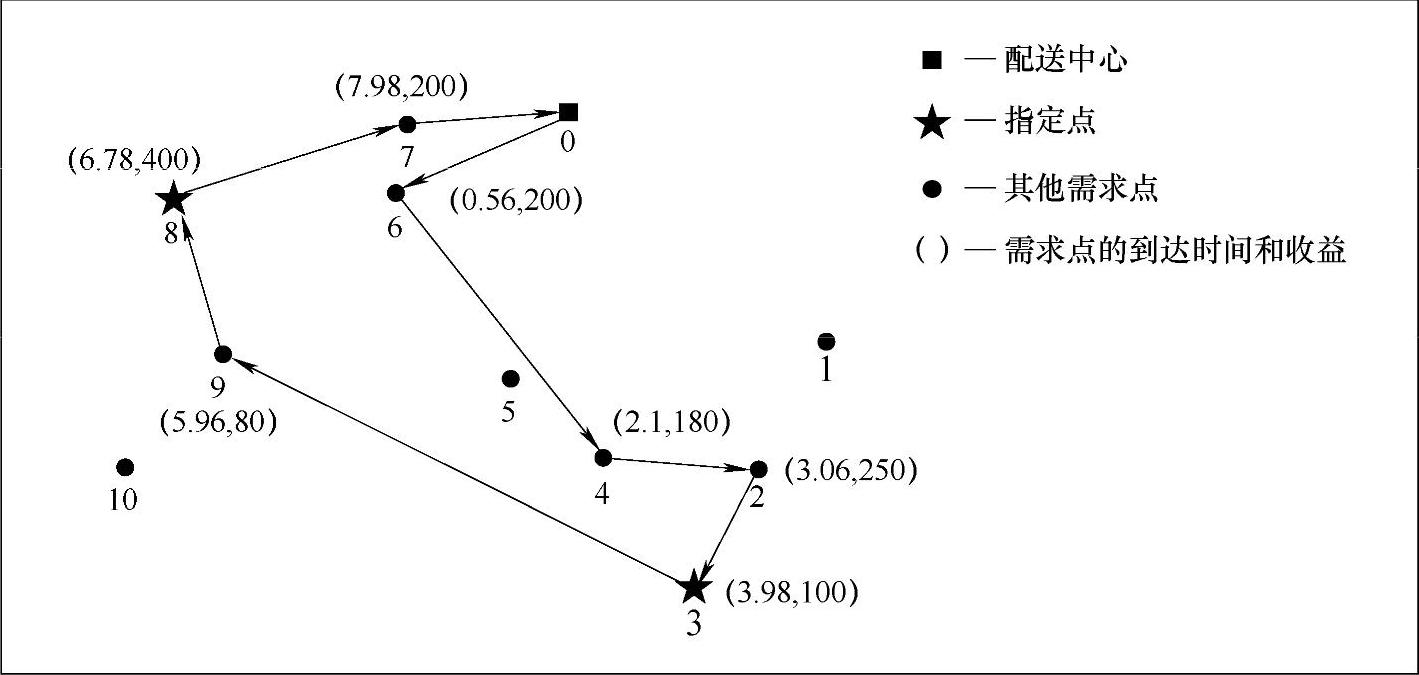
本例的问题规模不大，可以用精确算法进行求解。将上述的相关数据代入本节的整数线性规划模型中，利用Lingo软件编程求解得最优路径为0→6→4→2→3→9→8→7→0（如图10-3所示），相应的总收益为1410元。精确算法的计算时间为2h。精确算法求解的结果可以作为其他算法的评价依据。

(www.daowen.com)

图10-3 精确算法求解的最优路径

2.贪婪算法求解

先对指定点集中的点进行排序，因为指定点是必须被服务的，并且它们的路径顺序直接影响其他点的选取。本例中的指定点有v₃点和v₈点，由此得两条路径，p₁（v₀，…，v₃，…，v₈，…，v₀）和p₂（v₀，…，v₈，…，v₃，…，v₀）。按照路径顺序规则对它们进行可行性判别。因为e₃+τ₃+t₃₈=4.4∈[4，7]、e₈+τ₈+t₈₃=6.4∈[2，7]，所以路径p₁、p₂均可行。一般，需求点的时间窗越宽，路径优化的灵活性越高，反之则越低。比较指定点v₃和v₈，e₃<e₈，即v₃点的最早服务时间小于v₈点的最早服务时间，l₃=l₈，即v₃点的最晚服务时间等于v₈点的最晚服务时间。在路径p₁中，v₃点先于v₈点被服务，为了使两个指定点都可以在其时间窗内被服务，v₃点的时间窗变为[2，4.6]，v₈点的时间窗不变。在p₂路径中，v₈点先于v₃点被服务，v₈点的时间窗变为[4，4.6]，v₃点的时间窗变为[6.4，7]。路径p₁的灵活性高于路径p₂，因此可以优先考虑路径p₁。

指定点集将一条完整的路径分成了多个子路径，如v₃、v₈将路径p₁分成了三个子路径，p₁₁（v₀，…，v₃）、p₁₂（v₃，…，v₈）、p₁₃（v₈，…，v₀）。由于每个需求点的时间窗不同，优先选取的点会影响其他点的选取。本节问题的求解可以从路径的前端向后端进行。

对子路径p₁₁（v₀，…，v₃）：

1）p₁₁（v₀，…，v₃）是路径p₁（v₀，…，v₃，…，v₈，…，v₀）的子路径，为了使指定点v₈可以在其时间窗内被服务，被优先服务的v₃点的最晚服务时间变为l₃，=l₈-s₃-c₃₈=4.6，v₃点的时间窗变为[2，4.6]。

2）根据表10-3和表10-4，可以得到v₀的时间窗邻域{v₁，v₂，v₆，v₉，v₁₀}，进而得到地理邻域{v₁，v₆}。由于w₆＞w₁，且y₆+τ₆+t₆₃=2.54∈[2，4.6]，因此优先服务v₆点。v₀的紧后点为v₆，到达v₆点的时间y₆=0.56h。

3）同2），得到v₆的紧后点v₄，v₄的紧后点v₂，v₂的紧后点v₃，形成子路径p₁₁（v₀，v₆，v₄，v₂，v₃），到达v₃点的时间y₃=3.98h。

继续按照子路径p₁₁形成的启发式方法，得到子路径p₁₂（v₃，v₈）、p₁₃（v₈，v₇，v₀），从而得到问题的一个解，路径p₁（v₀，v₆，v₄，v₂，v₃，v₈，v₇，v₀），如图10-4所示，括弧内为相应需求点的到达时间和所获得的收益。路径p₁的总收益为1330元，回到终点时间为8.56h。贪婪算法的计算时间不足1s。

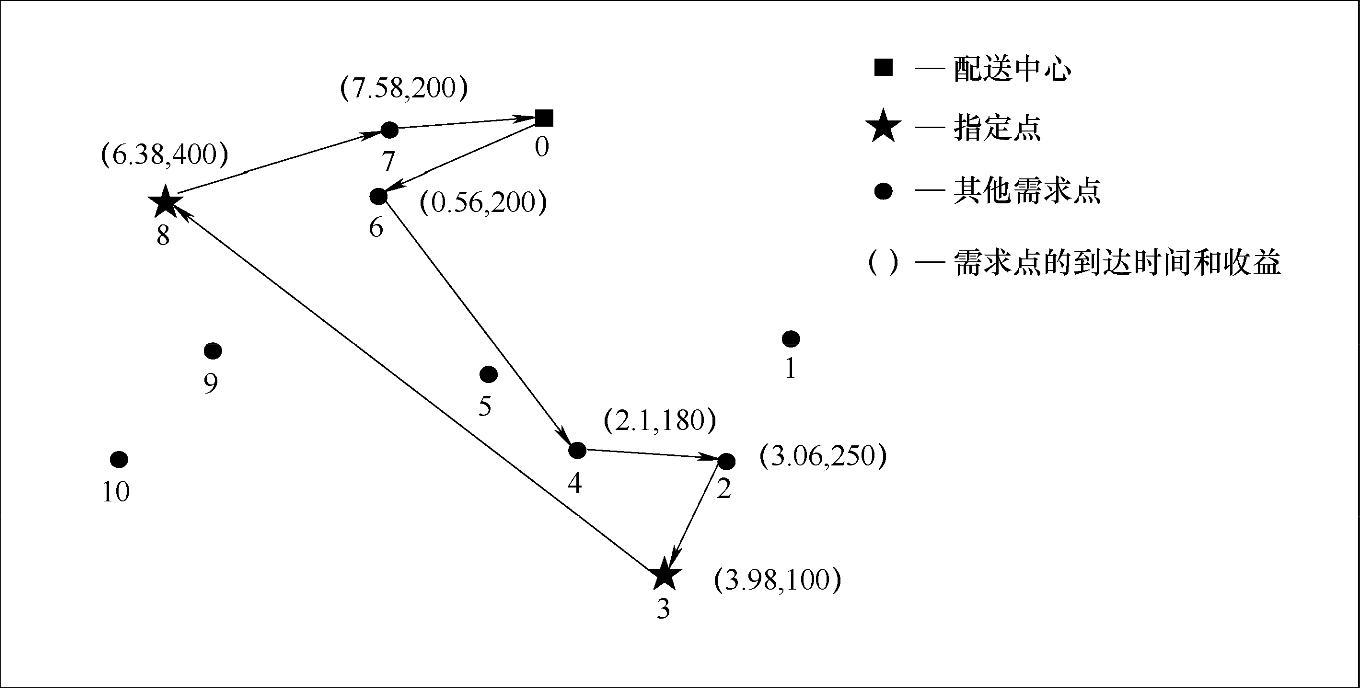
图10-4 贪婪算法的求解结果p₁

比较本小节的贪婪算法和精确算法的求解结果，可以看到，贪婪算法求得的解接近精确算法求得的最优解，精确度达94.3%，但前者的用时仅为后者的0.8%。这说明，精确算法适用于求解小规模、解的精度要求高的问题，启发式算法可以高效地求得较优解，适用于大规模、时间敏感的问题。