1.贪婪算法

在带指定点集和时间窗的定向问题中，每个需求点都有不同的时间窗和不同的收益，并且，指定点必须在其要求的时间内被遍历。针对问题的特点，带指定点集和时间窗的定向问题的贪婪算法主要利用路径顺序规则和优先规则改进解的质量，具体描述如表10-1所示。规则描述中的e_i、τ_i、y_i、l_j、t_ij分别表示v_i点的最早开始服务时间、v_i点的服务时间、A到达v_i点的时刻、v_j的最晚开始服务时间、v_i到v_j的所需时间。

表10-1 指定点集和时间窗的定向问题的启发式算法规则

时间窗邻域又称为时间窗可行域。如果从v_i点出发到达v_j点的时刻q_ij（q_ij=y_i+τ_i+t_ij，即到达v_i点的时刻、在v_i点的服务时间、v_i与v_j间的时间距离三者之和）在v_j的时间窗[e_j，l_j]内，则v_j点是v_i点时间窗邻域中的点，v_i点的时间窗邻域记为vⁱ_tw。v_i点的地理邻域可以定义为Vⁱ_tw中满足条件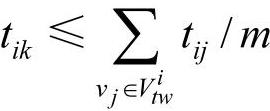的所有v_k点，其中m为v_i时间窗邻域Vⁱ_tw中点的个数。路径顺序规则和优先规则中的时间窗邻域保证了解的可行性，优先原则中的地理邻域则可以使收益大的点被优先服务，从而获得较优的解。

贪婪算法的基本流程：

1）优化指定点顺序。将指定点集排序，得到不同的路径，根据指定点的时间窗特点，选取路径优化灵活性高（时间窗相对宽裕）的路径，并修改指定点的时间窗。

2）顺序插入。对①中选取的路径，从起点开始优化。首先根据点的时间窗甘特图和点间的时间距离表得到当前点的时间窗邻域，进而由时间窗邻域得到当前点的地理邻域，选取地理邻域中收益最大的点作为当前点的紧后点。将当前点的紧后点作为新的当前点，继续选取它的紧后点，直到终点，从而形成一条完整的路径，得到问题的一个较优解。如果一个新点插入路径后，其紧后点为指定点，且从新插入点到达指定点的时间不在该指定点的时间窗内，则这个新点不能插入路径。

作为一种启发式算法，贪婪算法根据问题的特点，采用一些启发式规则求解问题，简便易行、计算时间短。贪婪算法既可以独立地作为一种求解方法，又可以与遗传算法融合，作为遗传算法中初始解的生成方法，并指导遗传操作。

2.遗传算法(www.daowen.com)

带指定点集和时间窗的定向问题的遗传算法设计方案如下：

1）编码。采用实数编码，在路径优化问题中也称序号编码、路径编码，如0→1→5→3→2→9→4→0表示一条从v₀点出发，依次经过v₁、v₅、v₃、v₂、v₉、v₄点，并最终回到v₀点的路径。这种编码方案最大的优点是易于解码。

2）初始种群。采用随机和启发式相结合的方法生成初始种群，一方面保证初始种群的多样性，另一方面使初始种群有较好的优良性。这里的随机生成法不同于一般的随机生成法，它是结合问题的特点，按时间顺序，同时考虑指定点集，从起点开始，按等概率选择当前点的时间窗邻域中的点作为其紧后点，再从紧后点的时间邻域中等概率选取紧后点的紧后点，一直到终点，形成一条完整的路径，也就是一个个体。随机体现在紧后点的概率选取上。启发式生成法指利用上一小节的贪婪算法先得到一个较优的解，然后对其进行多次微调，生成多个个体。随机和启发式生成法的比例为4：6，即随机法生成的个体数量占种群规模的40%，启发式法生成的个体数量占种群规模的60%。

3）适应度评价。将目标函数作为适应度函数，即适应度越大，总收益越大。

4）选择。最优解100%保留，而对其他个体则通过联赛竞争方法保留下来，进一步进行下面的交叉和变异操作。

5）交叉。在一条父代染色体上进行插入操作来产生新个体。一般的交叉操作是通过两条父代染色体彼此交换遗传信息产生子代。由于带指定点集和时间窗的定向问题有硬时间窗约束，这种遗传操作在实数编码下会产生大量不可行的个体，因而只在一条父代染色体上进行操作产生新个体，以提高算法的效率。具体操作是，从父代染色体的首个基因开始，也就是从染色体的首个基因开始，若当前基因的紧后基因不是其地理邻域中的基因，则以交叉概率p_m选择地理邻域中收益最大的基因插入到染色体中，否则不插入新基因，一直到染色体的最后一个基因，从而产生一个新染色体。若当前基因的紧后基因是指定基因，则不插入新基因。若当前基因的紧后基因的地理邻域中有指定基因，则100%选择指定基因，以保证插入操作中指定基因始终在染色体上。

6）变异。对每一染色体，即路径，随机选择变异点v_k，以变异概率p_m选取中收益最大的点作为v_k的新紧后点v^k_nn，替代v_k的原紧后点v^k_no，若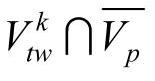为空集，则选择V^k_tw中除v^k_no以外的收益最大的点。由于每个点都有自己的时间窗，v^k_nn的加入可能导致路径中v^k_nn后面的部分点不可行。对v^k_nn后面的某不可行点，从其紧前点的时间窗邻域中随机选取新的紧后点，一直到终点。如果v^k_nn后面的点中有指定点，在选择紧后点时还必须保证指定点在个体中。V^k_tw为v_k点的时间窗邻域，V_p为路径p中的点的集合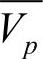，为非路径p的点的集合。

7）控制参数。种群规模为50；进化的代数最大为50；交叉概率p_c=0.9-（0.9-0.65）G/G_max，其中，G、G_max分别为当前进化代数、最大进化代数，交叉概率随进化代数的增加而较小；变异概率p_m=0.001+（0.01-0.001）G/G_max。变异概率随进化代数的增加而增大。动态的交叉和变异概率可以加快收敛速度，同时在一定程度上防止“早熟现象”的发生，提高收敛效果。