首先，通过一个实例引出本节要研究的问题。A是某物流企业的一支运输小分队，负责某一小片区域的配送。A每天早上接到配送任务后，先要制定相应的配送计划，然后，按照配送计划进行配送。A对其负责的区域很熟悉，如果遇到异常情况，如交通堵塞或限行，可及时做出调整。在A所服务的客户中，有一些是企业的重要客户或固定客户，有一些则是一般客户。A的每一配送任务都有时间窗，即在指定的时间窗内将货物送达客户手中。如果早于时间窗的最早时间，A需等待，这期间会产生等待成本；如果迟于时间窗的最晚时间，A需赔偿客户损失，还可能丧失客户。同时，由于客户的地理位置、配送量和配送时间要求等不一样，完成每一客户的配送任务给企业带来的收益是不一样的。此外，A在每一客户处为最终完成其配送任务需要花费卸货、验收等服务时间，不同的客户有不同的服务时间。基于以上情况和要求，A一般会在每日有限的时间内从接到的配送任务中选择部分任务完成，其中重要客户的配送需求必须满足，否则损失巨大，其他未选中的配送任务则由其他的运输分队完成或外包出去。A制订每日的配送计划时需要考虑的问题是如何优化配送路线，才能尽可能多地完成配送任务，使总收益达到最大。这是一个典型的带指定点集和时间窗的定向问题。

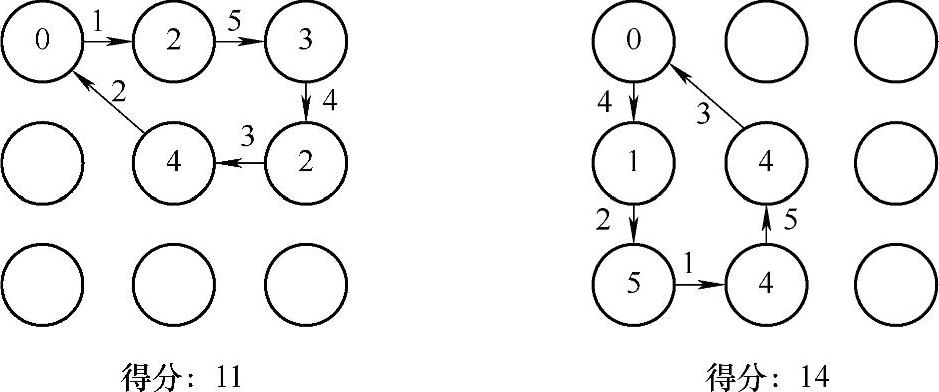
带指定点集和时间窗的定向问题可以用图论简单描述为：给定一个网络图G（V，E），V为点的集合，E为边的集合，每个点都对应一个相应的得分（可表示收益）、一个时间窗和一个服务时间，每条边都对应一个权重（可表示两点间的距离或行走时间），指定点集S是V的一个子集，是必须被遍历的点的集合。求一条从起点到终点的路径，在路径总边权不超过一定限制（如路程或时间），并且指定点集中的点均被遍历到的条件下，使得遍历过的点的总得分或总收益达到最大。图10-1表示了两条不同的配送路径对应的得分情况，其中0表示配送中心，其余为需求点。从图中可以看到，在满足约束条件的前提下尽可能多地遍历点，不同的路径包含不同的点，总收益也不同。图中，每个圆圈中的数字表示得分，边上的数字表示行走时间。

(www.daowen.com)

图10-1 定向问题两条不同路径的示意图