为了对算法进行测试，我们选取了由一个配送中心（编号为0），16个客戶（编号为1，2，…，16）构成的双需求集货-送货一体化车辆路径问题实例，如图9-5所示。假设配送中心和各个客戶之间的距离均已知，每个客戶均有集货和送货两种需求，需求量已知，配送中心现有4辆车，车容量均为65，车型相同，在各条道路上的运行速度相同，为30km/h，每辆车为一个客戶服务（卸货、装货）的总时间均为5min。各辆车运行1km的费用均是1元钱，各辆车每天从配送中心出发到返回配送中心的总运行时间不超过340min。各个客戶的需求量和供应量数据如表9-7。

图9-5 配送中心和16个客户的位置关系图

注：0为配送中位置，1-16为客戶的位置

表9-7 各个客户的需求量和供应量

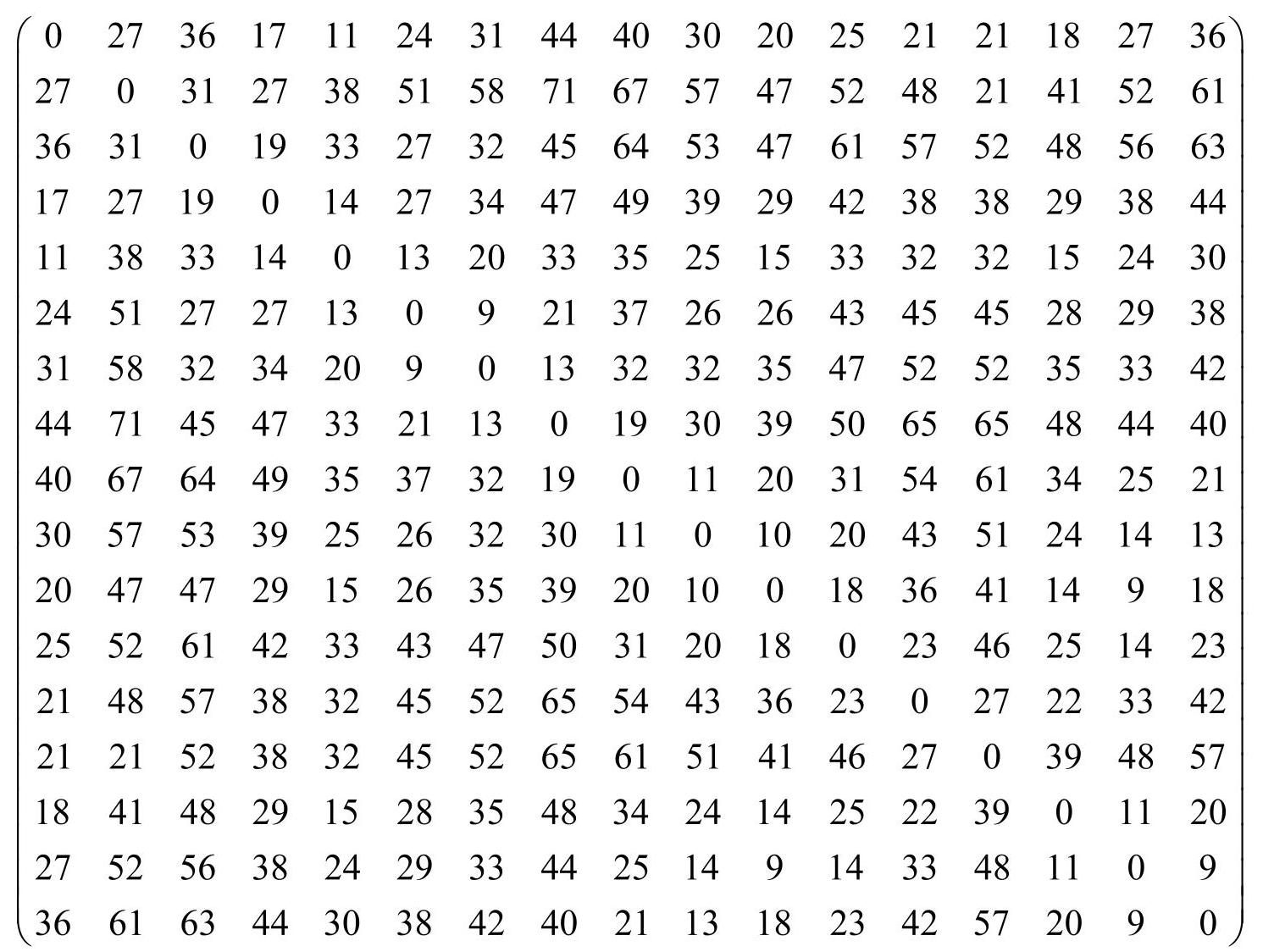
配送中心及客戶之间的距离矩阵为（单位：km）

(www.daowen.com)

直接利用Lingo软件编程，求解整数线性规划模型，可以得到整体最优方案（见图9-6）为：总费用343元，一共需要3辆车，每辆车的运行路线如表9-8及图9-6。

表9-8 计算得到的车辆运输路径表

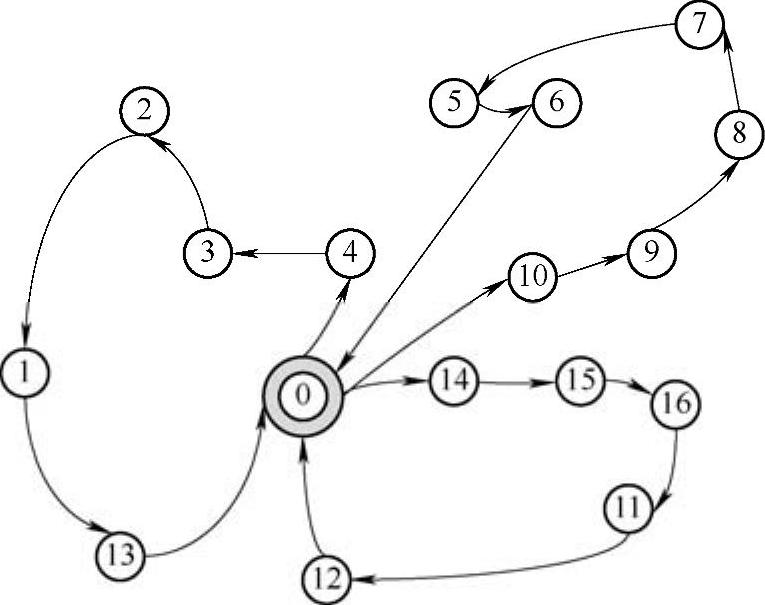
图9-6 计算结果

同时，我们也利用VC++编写了基于节约准则的启发式算法的计算程序，并利用程序对该实例进行了计算，同样可以得到表9-8及图9-6中的计算结果。