1.精确算法

虽然我们建立的模型为整数线性规划模型，但对于规模较小的问题，可以通过直接求解该整数线性规划模型得到全局最优解。为此，我们使用Lingo8.0软件编写了算法的实现程序，并利用算例做了计算测试。

2.启发式算法

由于具有总时间和车容量约束的双需求集货-送货一体化车辆路径问题（DVRPTWB）属于典型的NP-hard问题，当问题的规模较大时，直接求解整数线性规划模型需要的时间会比较长，因此，我们设计了一个基于节约准则的启发式算法。该算法的基本思想是将DVRPTWB中存在的两个满足合并条件的车辆运输回路（0，…，i，0）和（0，j，…，0）合并成一个车辆运输回路（0，…，i，j，…，0），使总运输成本下降，如图9-4所示。

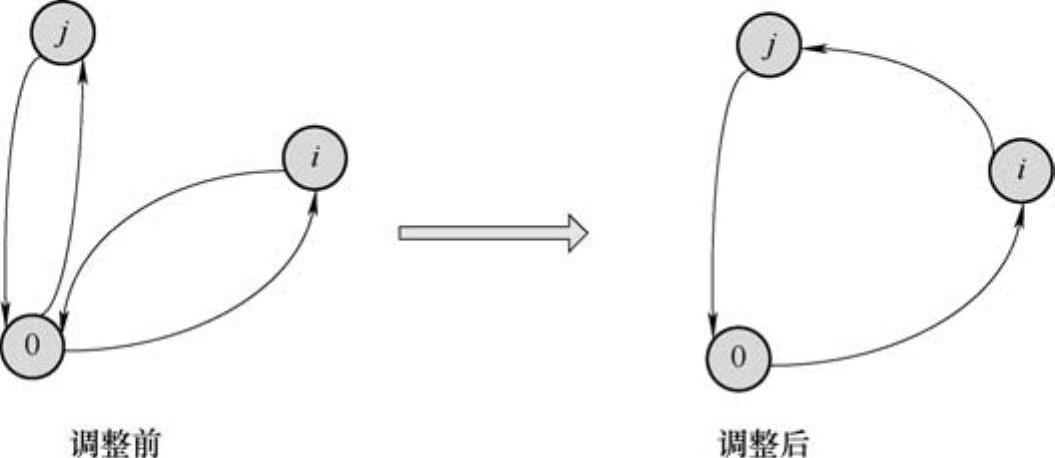
图9-4 基于节约准则的启发式算法的描述

注：调整前需要两辆车完成两个客户的集货送货任务，两辆车的运输回路分别为（0，i，0）和（0，j，0）；调整后只需要一辆车即可完成两个客户的集货送货任务，运输回路为（0，i，j，0）。

基于节约准则的启发式算法可以描述为以下三个步骤：

1）形成一个初始解。形成初始解时，需要满足所有的约束条件，例如车辆的容量限制、总时间限制等。初始解的形成方法很多，最简单的初始解是：为每个客戶单独安排一辆车完成配送及集货任务。假若此时仍然不能满足所有的约束，则意味着原问题无可行解。初始解形成后，可以得到每个车辆的一条初始运输回路。第k辆车的运输回路可以表示成：T_k={0，i，…，j，0}，k∈K，i，j∈D，其中，i，j表示客戶的序号。

2）计算节约度。对于任意两条不同车辆的运输回路，判断其是否符合合并的条件，如果符合，则计算合并后节约的成本，并对节约成本按照升序排列。例如：有两条不同的车辆运输回路T_r={0，…，i，0}，T_s={0，j，…，0}，仍然假设车辆k离开客戶t时的装载量为Q_tk，车辆k经过的所有客戶的总集货量为G_k，总送货量为H_k，总服务时间为t_k。在以下两种情况下，T_r和T_s可以合并。(www.daowen.com)

情况1：如果对于由车辆r服务的任意一个客戶u∈T_r，有Q_ur+H_s≤L_r成立；对于由车辆s服务的任意一个客戶v∈T_s，有Q_vs+G_r≤L_r，并且t_r+t¹_s≤e_r-s_r，其中t¹_s表示原先由车辆s服务的所有客戶如果换成由车辆r提供服务所需要的总时间（当车型相同的时候，可以认为t¹_s=t_s），则车辆r和车辆s的运输回路可以合并，并由车辆r完成合并后回路上所有客戶的集货及送货任务。

情况2：如果对于由车辆r服务的任意一个客戶u∈T_r，有Q_ur+H_s≤L_s成立；对于由车辆s服务的任意一个客戶v∈T_s，有Q_vs+G_r≤L_s，并且t¹_r+t_s≤e_s-s_s，则车辆r和车辆s的运输回路可以合并，并且由车辆s完成合并后回路上所有客戶的集货及送货任务。

对于任意两条可以合并的运输路线，按照下列公式计算合并后的成本节约值

Δc_ij=c_i0r+c_0jr-c_ijs+t_s-t¹_s

对计算结果进行升序排列。

3）进行运输回路的合并。选取成本节约值最大的两条车辆运输回路，不妨假设为T_r={0，…，i，0}和T_s={0，j，…，0}，如果成本节约值大于零，并且，一个回路以（i，0）结束，另一个回路以（0，j）开始，且满足情况1的条件（满足情况2的条件时可以按类似的方法合并回路），则这两条回路可以合并。回路合并时，删除这两条回路中的部分路径（0，j）和（i，0），然后，引入新的连接（i，j），得到新的回路（0，…，i，j，…，0）。同时，按如下规则修改相应的参数

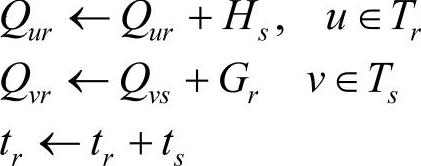
即由车辆r为合并后回路上的客戶提供集货-送货服务，将车辆s删除。重复2）和3）的计算，直到所有的回路都不能合并为止。