首先定义如下符号：

K={1，2，…，m}：表示车辆集合；

D={1，2，…，N}：表示客戶集合；

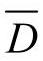D={1，2，…N}∪{0}={0，1，2，…，N}：表示扩展的客戶集合，其中0表示配送中心；

c_ijk：表示车辆k从客戶i点到达客戶j点的行驶成本，i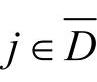，，k∈K；

t_ijk：表示车辆k从客戶i点到达客戶j点的行驶时间，i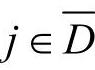，，k∈K；

τ_i：表示在客戶i处完成卸货、装货任务需要的总时间，i∈D，特别地，τ₀=0；

s_k：表示车辆k从配送中心出发的最早可能时间，k∈K；

e_k：表示车辆k返回配送中心的最晚收工时间，k∈K；(www.daowen.com)

L_k：表示车辆k的最大载重量，k∈K，如果所有车辆的容量相同，则L_k为常数；

p_i：表示客戶i的供应量，i∈D；

q_i：表示客戶i的需求量，i∈D。定义如下决策变量

Q_jk：表示车辆k离开客戶j时的装载量，其中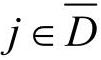，k∈K则DVRPWTB可以表示成如下整数线性规划模型

其中，目标函数表示完成所有的集货-送货任务的总运行成本最小；约束条件（9-21）和（9-22）表示每一个客戶恰好有一辆车为其服务；约束条件（9-23）表示为客戶i服务的车辆数等于离开该客戶的车辆数；约束条件（9-24）表示车辆k从经过的所有客戶处收到的货物总量不超过该车的总装载量；约束条件（9-25）表示车辆k服务的所有客戶需求的货物总量不超过该车的总装载量；约束条件（9-26）表示车辆k离开配送中心时的装载量不超过该车的总装载量；约束条件（9-27）和（9-28）表示车辆k离开客戶j时的装载量等于该车到达客戶j时的装载量减去客戶j的需求量加上客戶j的供应量；约束条件（9-29）表示车辆k离开客戶j时的装载量不能超过容量限制；约束条件（9-30）表示车辆k返回车场的时间限制；约束条件（9-31）和（9-32）为变量的取值约束。

文献中研究带集货和送货任务的VRP解法时，通常将问题划分为两个步骤进行求解，第一步是先确定客戶的分组，每一组客戶由一辆车为其提供服务；第二步是确定各组的车辆路径。这样做只能得到问题的近似解。我们在考虑这个问题时，没有将分组和确定车辆路径作为两个独立的问题考虑，而是统一在一个模型中。在我们的模型中，车辆集合可以包括车场拥有的所有车辆，最优解中不一定动用所有的车辆。如果某辆车对应的变量x_0k=0，则表示这辆车并没有使用。这样，我们在确定最优车辆路径的同时也解决了需要多少辆车的问题。另外，当我们把每辆车出动的固定成本考虑在内时，只需要在目标函数中加上车辆出动的固定成本，就可以得到包括车辆固定费用在内的总费用最小的车辆路径问题的最优解。包括车辆出动固定成本在内的目标函数可以表示成下列形式

式中，d_k表示车辆k每次出动的固定成本。

由于车辆的数目会直接影响到变量及约束的个数，因此，我们也可以事先对需要的车辆数的上界做一个估计，由于车辆数不会超过客戶的数目，因此，我们只需要使用不超过客戶数目的车辆数建立模型即可求出最优解。