1.实例

某集货中心拥有若干辆集货车为10个需求点提供集货服务。序号1表示集货中心，序号2～11表示需求点，每辆集货车的最大装载量为Q=50t，集货车在行驶过程中所花费的成本与所行驶时间成正比例，比例系数a=30。假设集货中心从下午14点开始上班，到18点下班，所有集货车都必须在下午14点到18点之间返回集货中心。每天的交通高峰时间段为下午17点到18点，集货车在非高峰时间段的行驶速度为50km/h，在高峰时间段的行驶速度为30km/h，集货中心与各个需求点之间的距离、各个需求点的需求量及集货车为各个需求点服务的时间等分别如表9-4和表9-5所示，求动用集货车数量最少且总成本最低的集货车行驶路径。

表9-4 集货中心与各需求点之间的距离 （单位：km）

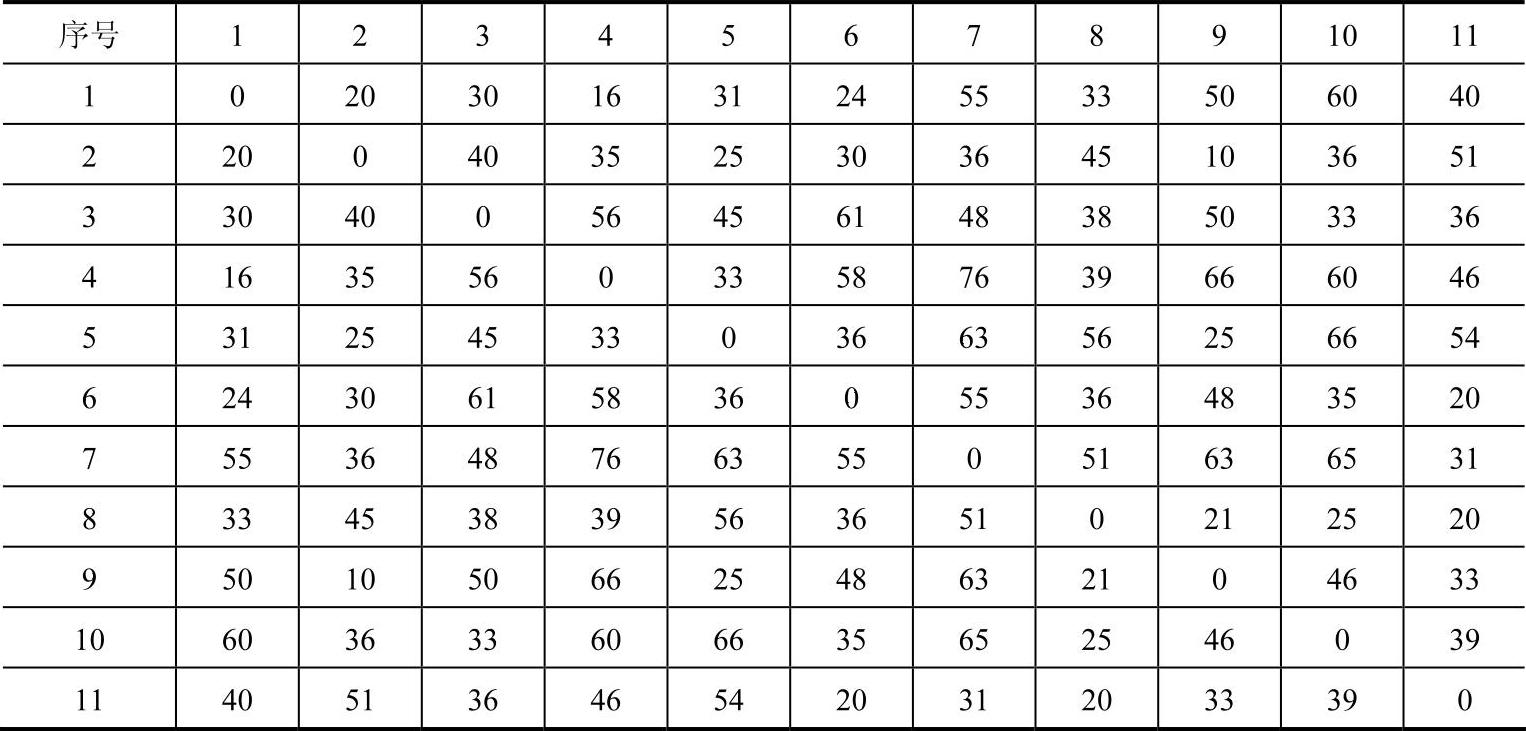
表9-5 各需求点的需求量和对应的集货服务时间

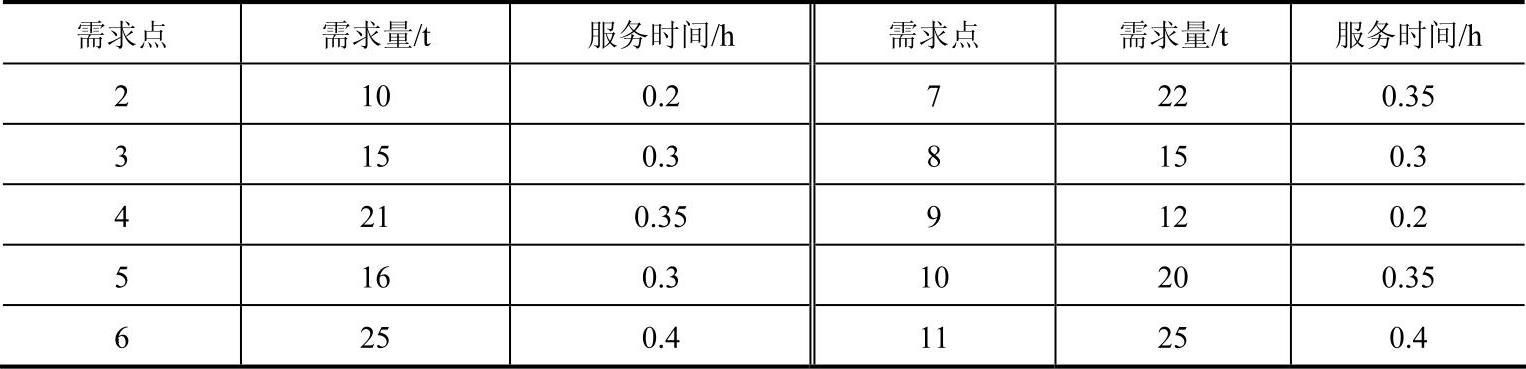
2.利用遗传算法求解的结果

（1）传统遗传算法的求解结果

本节利用Matlab软件编写了传统遗传算法的实现程序，算法的参数设置为：交叉率为0.8，变异率为0.01；初始种群数为200，最大遗传代数为200，经过计算，得到最优解与进化代数的关系图，如图9-2所示。

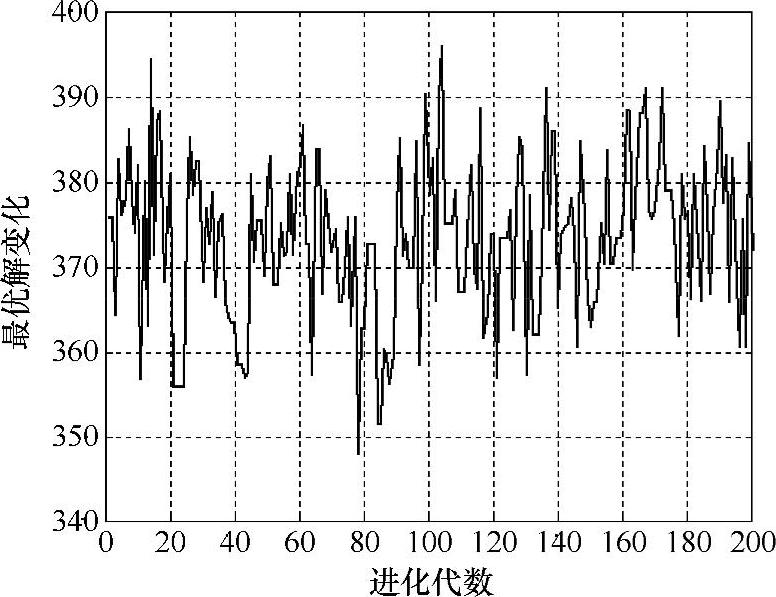
图9-2 利用传统遗传算法求解的结果

由图9-2可以看出，经过200代的进化仍然没有收敛，进化过程中得到的最优解为：共需动用4辆集货车，集货车总行驶时间为11.5967h，行驶过程所花费的总成本为347.9元，4辆集货车的行驶路径分别为1→4→1、1→7→11→1、1→5→2→9→8→1、1→3→10→6→1。(www.daowen.com)

（2）改进遗传算法的求解结果

利用Matlab软件编写改进遗传算法程序，参数设置为：初始种群为200，最大的遗传代数为200，经过计算得到的最优解与进化代数的关系如图9-3所示。

由图9-3可以看出，经过大约90代进化就能得到稳定的最优解，最优解为：共需动用4辆集货车，集货车的总行驶时间为11.4567h，行驶过程所花费的总成本为343.7元，4辆集货车的行驶路径分别为1→4→1、1→7→11→1、1→8→10→3→1、1→6→5→9→2→1。

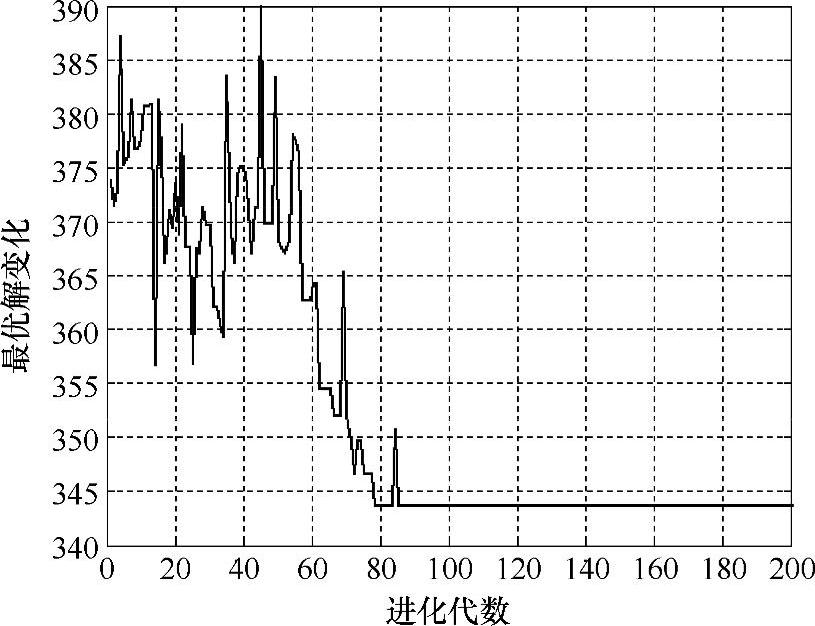
图9-3 利用改进遗传算法求解的结果

（3）两种遗传算法的计算结果对比

利用两种遗传算法经过200代进化得到的解的情况对比如表9-6所示。

表9-6 两种遗传算法的计算结果对比

从表9-7可以看出，无论从最优解、最差解还是平均解对应的目标函数值来看，由改进遗传算法计算得到的结果均优于传统遗传算法。特别是改进遗传算法具有很好的收敛性，而传统遗传算法不具有收敛性。