下面我们将分别设计求解带时间限制的车辆路径问题的两种遗传算法——传统遗传算法和改进遗传算法。

1.传统遗传算法

（1）解的结构

本节仍然采用自然数编码表示解的结构，1表示集货中心，2～11表示需求点，如（1 3 6 9 1 4 8 2 10 5 1 7 11 1）表示本次集货过程共动用三辆集货车，集货车行驶路径分别为1→3→6→9→1、1→4→8→2→10→5→1、1→7→11→1。

（2）遗传编码

为了避免交叉变异过程产生不可行解影响整体解的质量，本节把每代产生的解中的集货中心去掉进行编码，如上面的编码可表示为（3，6，9，4，8，2，10，5，7，11），再进行选择、交叉、变异，然后再把得到的编码根据约束条件重新表示成解的结构。

（3）适应度值计算

由于本节要求目标函数的最小值，所以定义适应度值为一个合适的值减去目标值，然后根据公式F（x_i）=f（x_i）/∑f（x_i） 计算适应度值。

（4）选择

本节采用轮盘赌法选择个体，产生新种群。

（5）交叉

为了保持个体对应解的可行性，本节采用部分匹配交叉法。如

交叉点在每代的交叉过程中随机生成，交叉后生成的新个体为

新个体1：11 6 9 5 7 10 3 4 8 2(www.daowen.com)

新个体2：7 3 6 4 8 2 11 10 9 5

（6）变异

为了避免产生不可行解，本节采用对换变异法，如

其中的对换点在个体中随机产生。

（7）终止规则

本节设置进化代数N作为终止规则，当进化代数达到N时，终止计算，并把历代种群中出现的适应度值最大的个体作为问题的最优解输出。

2.改进的遗传算法

针对上面给出的传统遗传算法，通过对交叉、变异过程的规则加以改进，可以设计出改进的遗传算法，改进的规则如下：

（1）交叉过程

在改进的遗传算法中，不设置交叉率参数，而是在每代种群中，优先在不同的个体中进行交叉，以便扩大种群的多样性。具体操作方法是：首先对种群里的所有个体进行随机排序（其中相同个体排在一起），然后对所有的i=1，2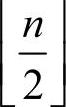，…，，判断序列中的第i个和第n-i个个体是否相同，如果不相同，则进行交叉，如果相同则不交叉。

（2）变异过程

本节不设置变异率参数，而是按照下列规则对交叉后的种群进行分析，决定是否对该种群的部分个体进行变异操作。

如果交叉后种群整体质量（可以用种群适应度平均值表示）优于交叉前（上代）的种群，则不进行变异操作，直接进入下一代。如果交叉后种群整体质量低于交叉前（上代）种群，则按顺序对适应度值没有超过交叉前种群适应度平均值的个体进行变异，若对某个个体进行变异后种群整体质量优于交叉前种群整体质量，则对该个体执行变异操作后直接进入下一代；若对某个体变异若干次（本文设置次数为10）后其适应度值还是低于交叉前（上代）种群适应度的平均值，说明该个体不好，则淘汰该个体，并用交叉前（上代）的最优个体替换该个体；若替换后种群总体质量还是不如交叉前（上一代），则对下一个适应度值低于交叉前（上代）种群适应度平均值的个体再进行变异，依次类推，直到变异后种群整体质量优于交叉前（上代）的种群，进入下一代。