设有一配送中心为10个客戶提供货物配送服务，序号0表示配送中心，序号（1，2，…，10）表示10个需求点。配送中心共有6辆同型号的车辆，每辆车的最大装载量均为Q=90t，每辆车的最长行驶距离均为D=200km，动用每辆车的固定成本均为50元，每辆车行驶每公里的成本均为20元，配送中心及各个需求点之间的距离见表9-1，车辆在配送中心及各个需求点之间的行驶时间见表9-2，各个需求点的需求量、服务时间及可利用的时间窗见表9-3，为了使总配送成本达到最少，需要安排多少辆车完成配送任务？每辆车的配送路径是什么？

表9-1 配送中心与各需求点之间的距离 （单位：km）

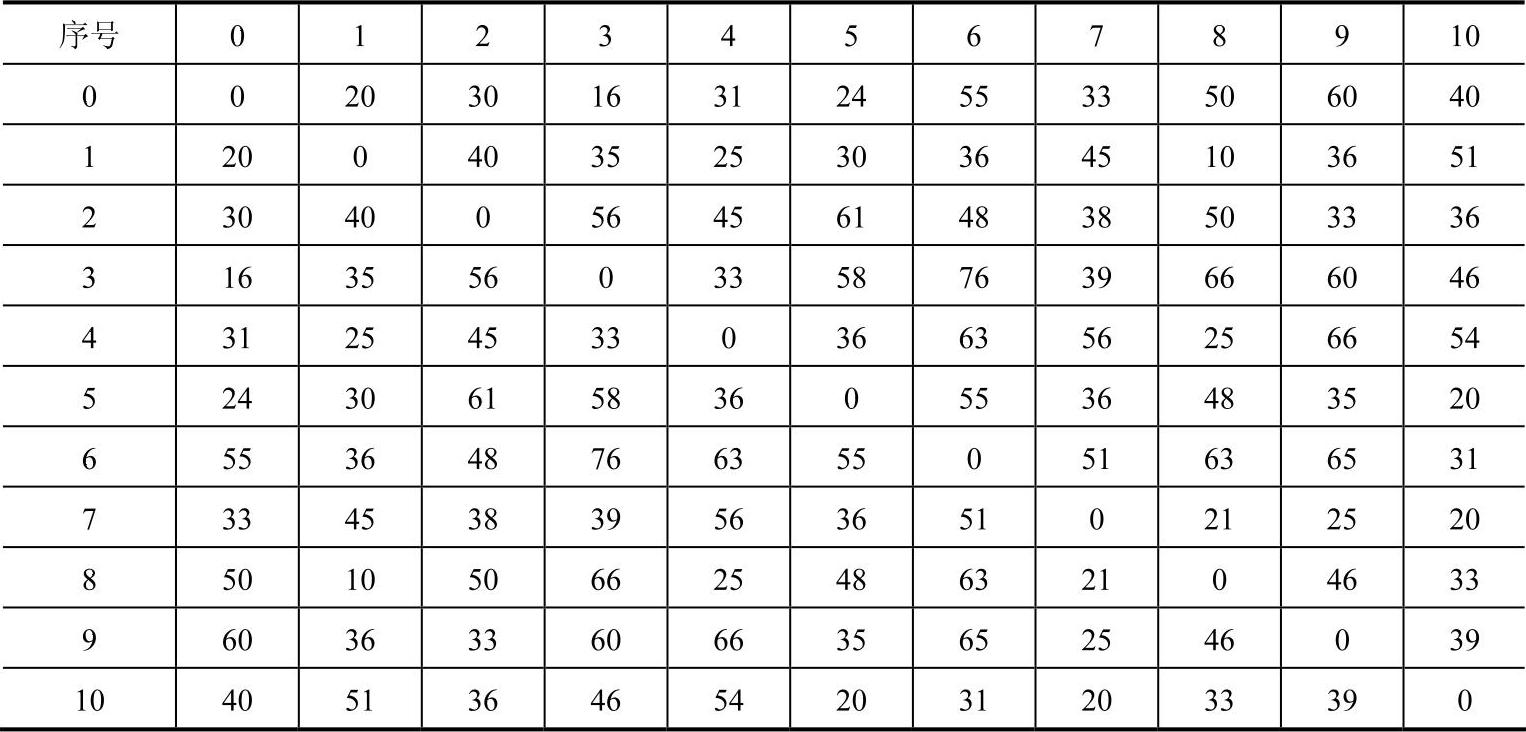
表9-2 车辆在配送中心及各需求点之间行驶的时间 （单位：h）

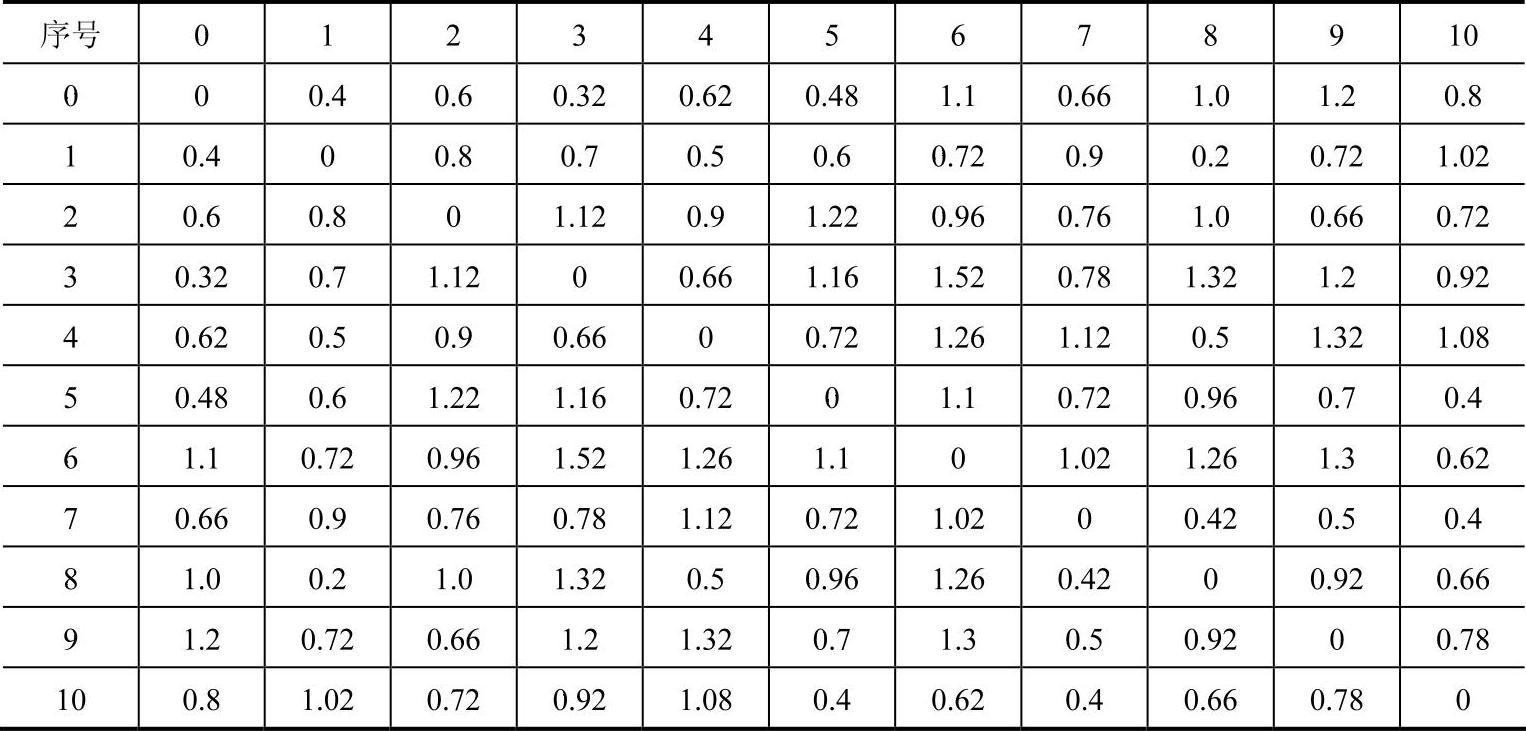
表9-3 各需求点的需求量与服务时间和可利用时间窗(www.daowen.com)

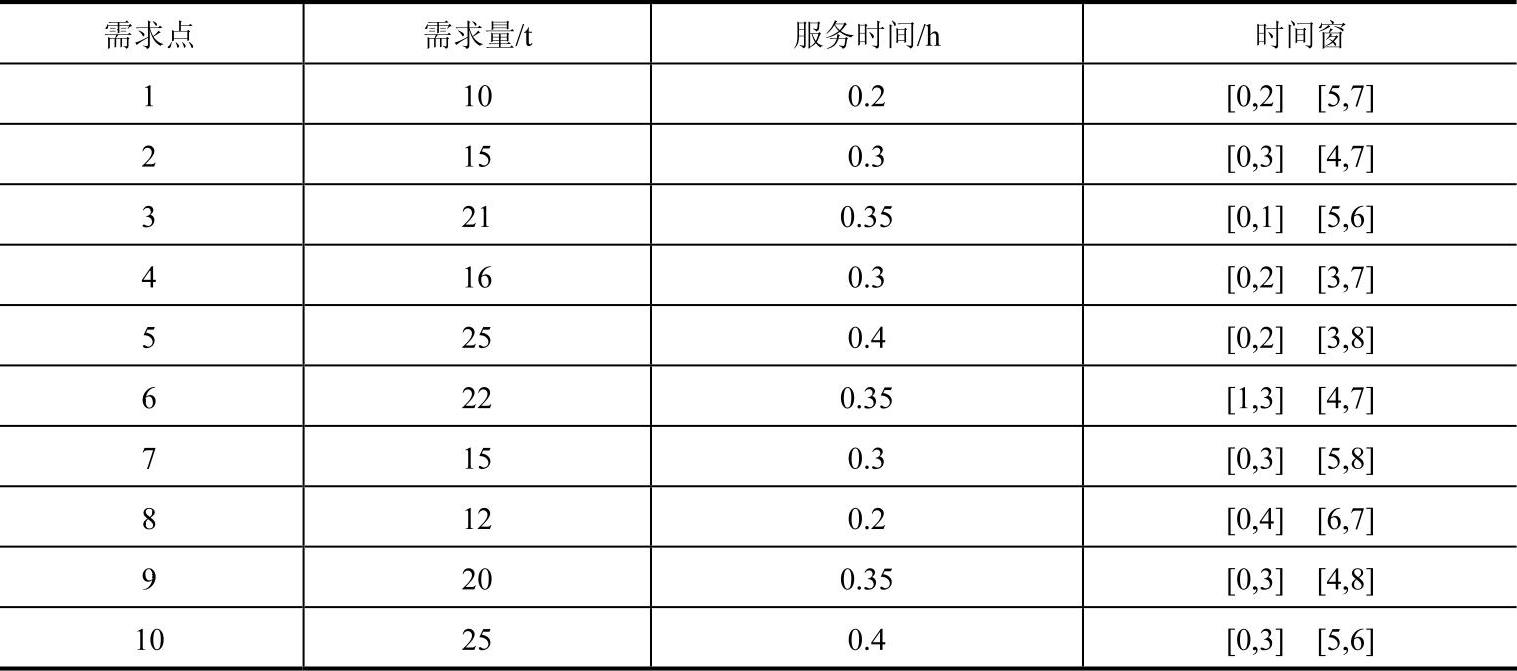
对于以上问题，首先用Lingo软件编写程序，在Windows XP（P4，1.6G，1G内存）环境下运行程序，求解整数线性规划模型，经过大约5h的运算，得到精确最优解，共需要动用3辆配送车，配送路径分别为0→2→9→7→8→4→0、0→1→6→10→5→0、0→3→0，总行驶距离为328km，总配送成本为6710元。

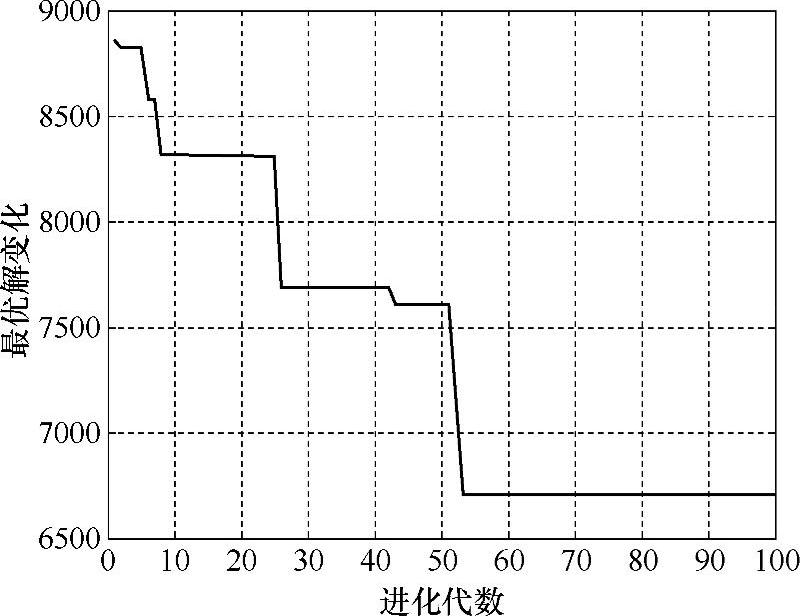
表9-1 遗传算法收敛过程曲线

由于直接求解整数线性规划模型用时太长，接下来，我们用遗传算法求解该问题。利用Matlab编写遗传算法程序代码，设置种群规模为200，最大进化代数为100，在Windows XP（P4，1.6G，1G内存）环境下运行遗传算法程序，共进行了20次计算，平均运行时间约为14.5s，20次运算得到的动用车辆数均为3辆，与精确最优解相同；20次运算得到的平均行驶距离为338km，平均总成本为6914元。遗传算法得到的平均行驶距离及平均总成本与精确最优解的偏差比例约为3%o图9-1是我们记录的其中一次遗传算法的收敛过程曲线。从图9-1中可以看出，大约进化到50多代时便得到问题的最优解，由于在遗传算法中采用了最佳保留机制，因此，一旦得到问题的最优解，在接下来的进化过程中，目标函数值便不会再发生变化，即最优解会一直被保留到计算结束。所以，本节的遗传算法求解效率较高，可以用来求解大规模的问题。