某公司经销一种产品，设有三个加工厂A₁，A₂，A₃，每日的产量分别为12t、8t、20t。该公司把这些产品分别运往四个需求地B₁，B₂，B₃，B₄，各个需求地每日需求量分别为10t、6t、8t、16t。已知从各工厂到各需求地的单位运价如表8-17所示，从各工厂到各需求地的距离如表8-18所示，假设各个工厂的装车速度均为4t/h，各条路线上的空载行驶速度均为100km/h，若各条路线上的附加运输时间与运量之间的关系均为t¹_ij=f（x_ij）=0.5x_ij，问该公司应该如何安排调运，才能在14h之内，完成调运任务且使总费用最低？

表8-17 单位运费表 （单位：百元/t）

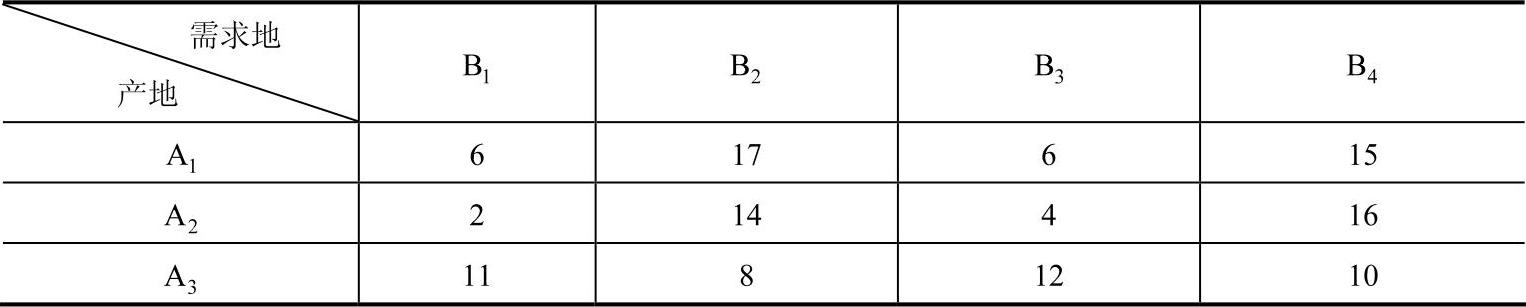
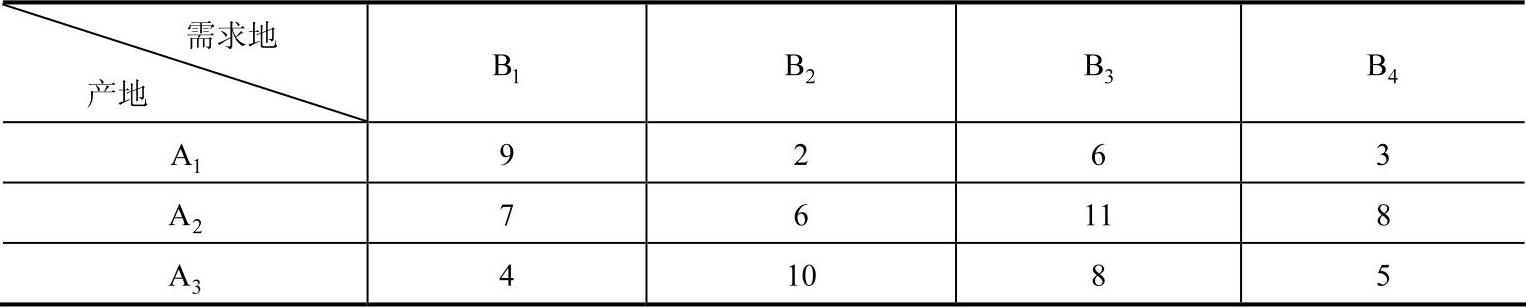
表8-18 距离表 （单位：100km）

解：首先，根据公式t⁰_ij=a_i/u_i+d_ij/v_ij计算出与运量无关的运输时间t⁰_ij，结果如表8-19所示。

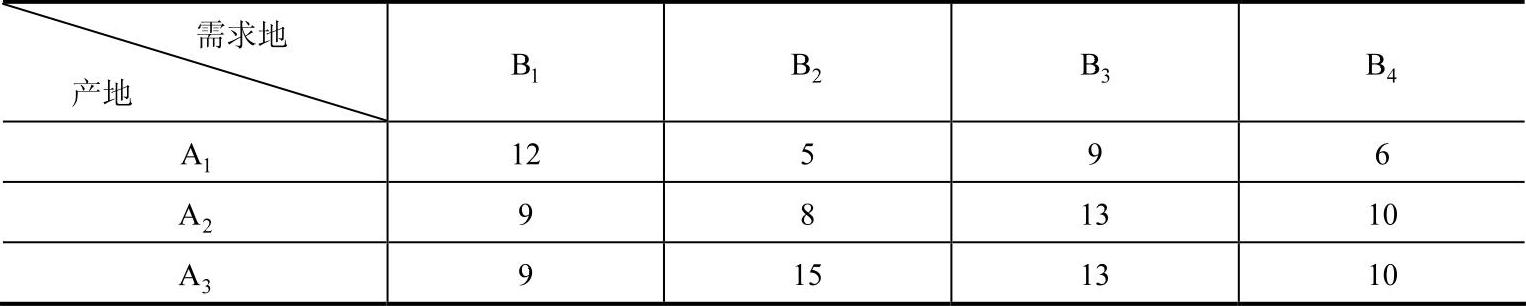
表8-19 各个产地到需求地与运量无关的运输时间t⁰_ij （单位：h）

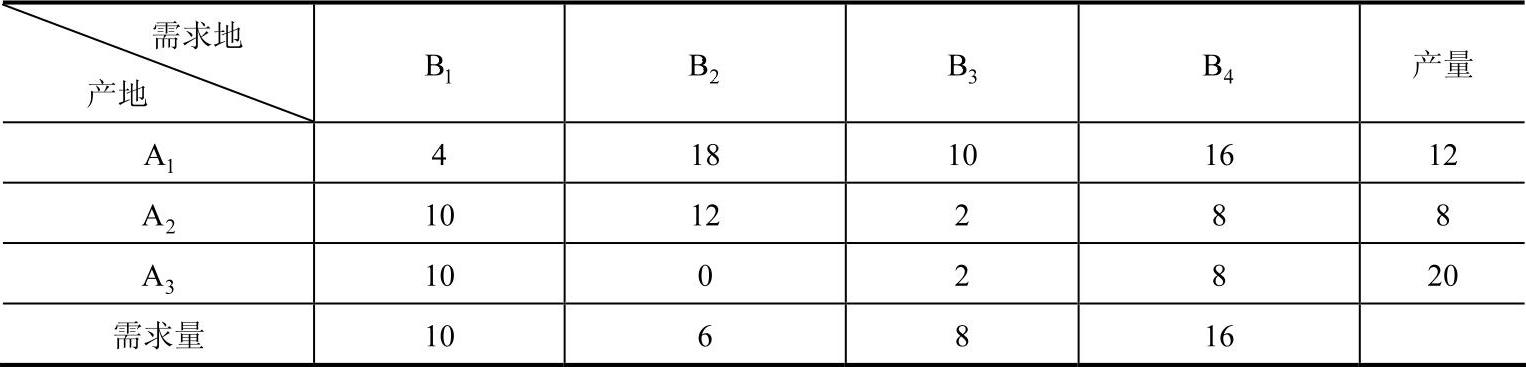
然后，令t^s_ij=max{0，14-t⁰_ij}，据公式0.5x_ij≤t^s_ij计算出各条路线上的货物运输量上限b_ij，计算结果如表8-20所示。

表8-20 各条路线上的货物运输量上限b_ij （单位：t）

根据表8-20和表8-17的信息构造网络图，如图8-2所示。其中每条弧旁边的数字表示容量和单位运费，记为（b_ij，c_ij）。在此网络图中，由于容量为零的弧（如A₃到B₂）对应的路线上运输时间超过14h，因而该路线上不可能安排运输，故没有表示出来。

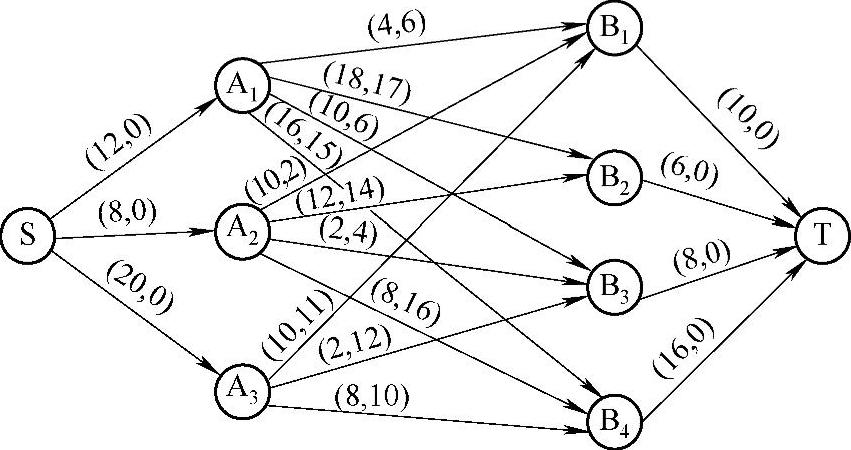
图8-2 根据表8-20和表8-17的信息构造的网络图

注：每条弧旁边的数字表示（容量，单位运费）

然后，用最小费用最大流算法求解图8-2中的网络最小费用最大流。求解步骤如下：

1）从f₀=0开始，构造加权网络图W（f₀），如图8-3。由Floyd算法求出图8-3中从S到T的最短路为S→A₂→B₁→T。根据最短路上各弧容量，将流量调整到f₁=8，各条弧上的流量值见图8-4。

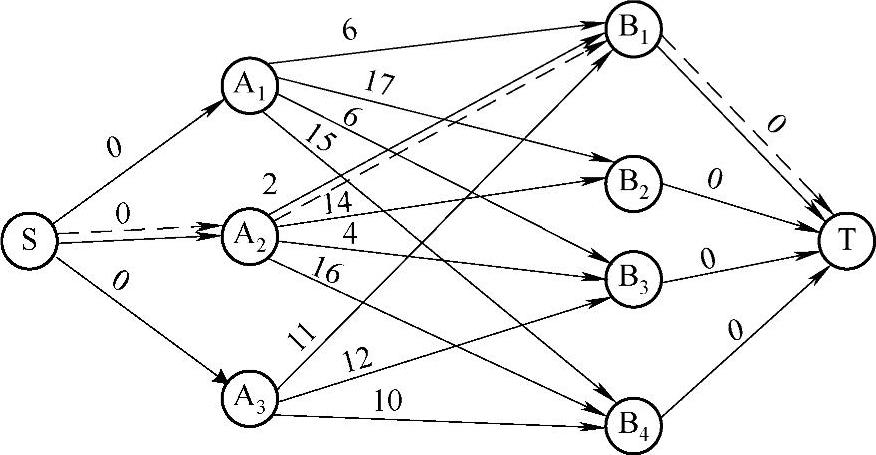
图8-3 加权网络图W（f₀）

注：其中每条弧旁边的数字表示单位运费，虚线对应最短路径。(www.daowen.com)

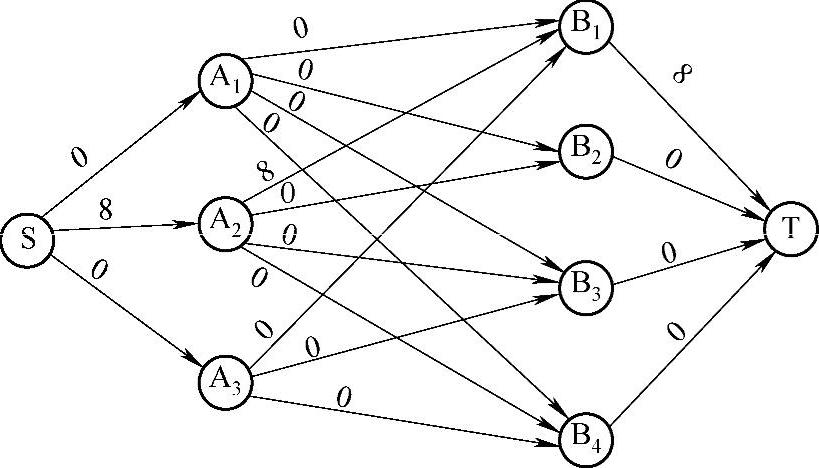
图8-4 第一次调整后的网络流量图f₁=8

注：弧旁边的数字表示流量。

2）构建加权网络W（f₁），见图8-5。由Floyd算法求出从S到T的最短路为S→A₁→B₃→T，先调整增广链上的流量，并使f₂=16，见图8-6。

3）继续重复上述过程，中间步骤省略，在W（f₉）中用Floyd算法已找不到S到T的最短路，故f₉=40为图8-1中从S到T的最小费用最大流，见图8-7。

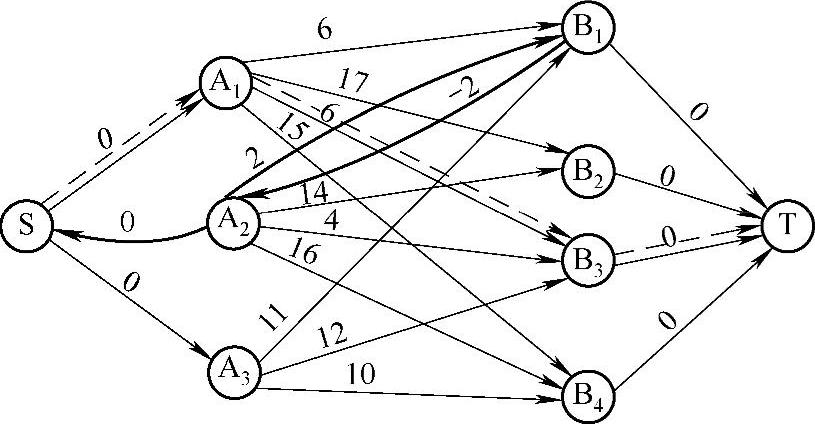
图8-5 加权网络图W（f₁）

注：弧旁的数字表示单位运费，虚线对应最短路径。

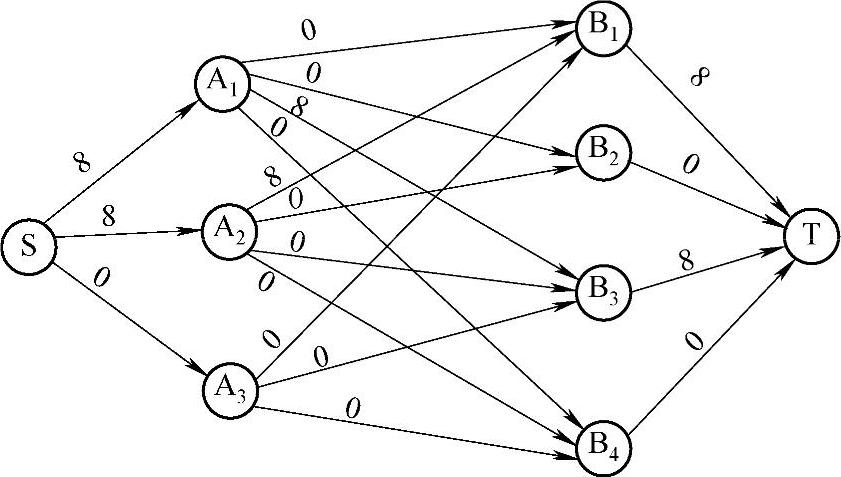
图8-6 第二次调整后的网络流量图f₂=16

注：弧旁边的数字表示流量。

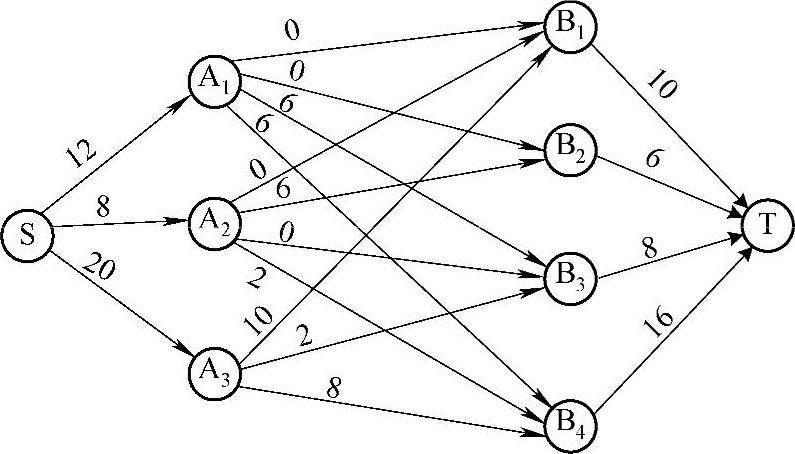
图8-7 第九次调整后的网络流量图f₉=40

注：弧旁边的数字表示流量。

在图8-8中不存在从S到T的路，故图8-7对应的即为网络的最小费用最大流，由于该最大流的流量等于总产量，因此，图8-7中对应的即为14h内完成调运任务的最小费用运输方案，其总运费为456百元。

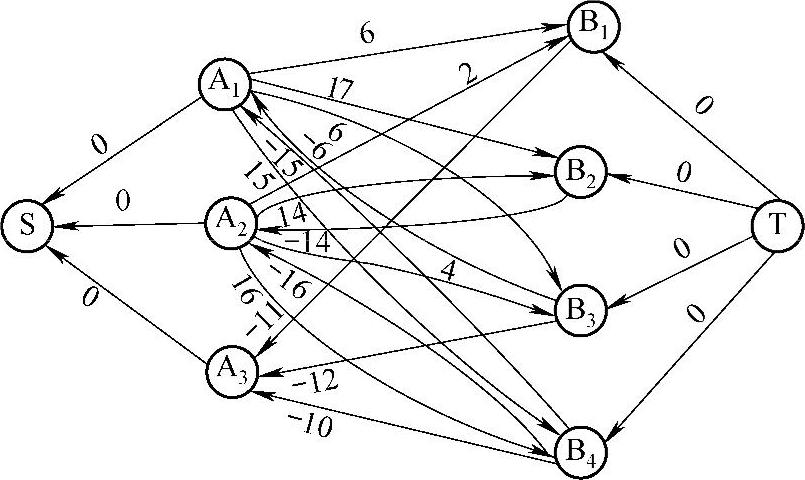
图8-8 加权网络图W（f₉）

注：弧旁的数字表示单位运费。