由8.2节的讨论可知，带时间限制的最小费用运输问题的约束条件非常特殊，因而可以通过巧妙的转化，构造一个网络图，根据运输时间的限制，求出各条路线上的运量上限，从而将问题转化为网络上的最小费用最大流问题，进一步借助于最小费用最大流问题的算法求出原问题的最优解，或证明原问题无可行解。

给定一个带时间限制的产销平衡最小费用运输问题，假设有m个产地A₁，A₂，…，A_m，各个产地的产量分别为a₁，a₂，…，a_m；n个需求地B₁，B₂，…，B_n，各个需求地需求量分别为b₁，b₂，…，b_n。已知各个产地A_i到各个需求地B_j的距离为d_ij、单位运费为c_ij、从各个产地到各个需求地的运输时间限制为T，则可以按照下列步骤将其转化为最小费用最大流问题。

1）根据给定的问题构造网络图。

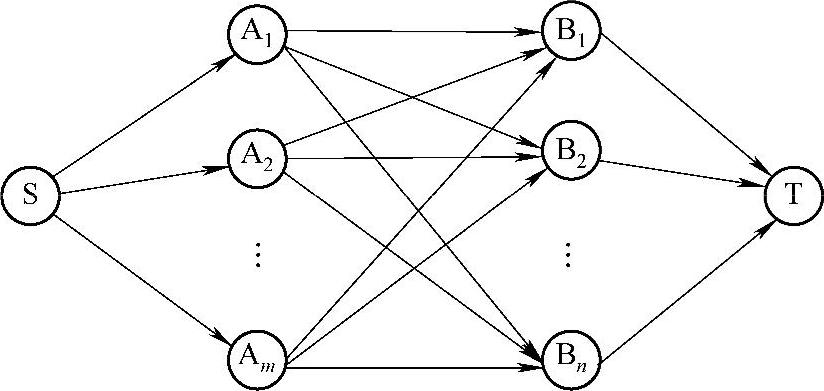
网络图中包括m+n+2个点（见图8-1），其中A₁，A₂，…，A_m对应原问题中的m个产地，B₁，B₂，…，B_n对应原问题中的n个需求地，S为虚拟的货物总发点，T为虚拟的货物总收点。

(www.daowen.com)

图8-1 带时间限制的最小费用运输问题对应的网络图

弧SA_i上的容量为a_i，单位运费为0；弧B_jT的容量为b_j，单位运费为0；弧A_iB_j上的单位运费为c_ij，容量为b_ij，b_ij的取值需要根据各条弧的实际情况确定。

2）计算各条弧A_iB_j上的容量b_ij。首先，利用公式t⁰_ij=a_i/u_i+d_ij/v_ij求出从产地A_i到需求地B_j运输过程中与运量无关的时间项t⁰_ij。然后，令t^s_ij=max{0，T-t⁰_ij}，根据f（x_ij）≤t^s_ij算出在时间T内可以从弧A_iB_j上运输的最大货物量，即弧A_iB_j上的容量b_ij。显然，对于t⁰_ij≥T的弧A_iB_j，t^s_ij=max{0，T-t⁰_ij}=0，因此，其容量为0。

3）利用最小费用最大流算法^[59]求出网络的最大流，若最大流的流量等于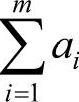，则其恰好对应带时间限制的运输问题总费用最低的调运方案；若最大流的流量小于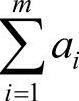，则说明原运输问题无可行解，即在规定的时间限制内无法完成调运任务。