一般运输问题的目标函数是总运费最低，由于现实中很多货物（如生鲜农产品）的在途运输时间不能太长，如果运输时间太长会发生变质腐烂等现象，造成更大损失；再比如救灾物资，只有赶在一定的时间内运到受灾地点才能发挥作用。因此，在安排这类物资的运输方案时，就必须考虑时间限制，寻找在一定时间内完成调运任务的方案，并且使总费用最低，这就是带时间限制的最小费用运输问题。假设允许的最长在途运输时间为T，则带时间限制的最小费用运输问题还应该满足下列约束

式中，t_ij表示从产地A_i到销地B_j实际运输物资所用的时间；T是在途运输所允许的最长时间。

虽然传统的运输问题总存在最优解，但是带时间限制的运输问题却不一定存在可行解。

在实际中，产地发货通常有两种形式，一种是产地按一定的先后顺序发货，完成调运所需要的时间为某产地往各销地发货时间的总和的最大值，即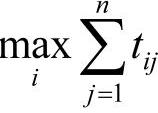；另一种是产地同时进行发货，实际调运所需要的时间为各产地往各销地发货时间的最大值，即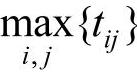。本节讨论的是产地同时发货的情况。

各产地往各销地运输货物的总时间包括装卸时间、从产地到销地的空载运输时间和受运输量影响的附加运输时间三部分。其中，前两部分是与运输量无关的常数，可以合并表示成t⁰_ij，第三部分与运输量有关，可以表示成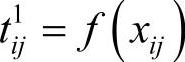。产地A_i到销地B_j所用的实际运输时间t_ij可以表示为(www.daowen.com)

式中，u_i表示产地A_i的装卸速度；d_ij表示从A_i到B_j的距离；v_ij表示从A_i到B_j空车行驶速度。

用x_ij表示从产地A_i运到销地B_j的货物量，则带时间限制的运输问题可以表示成下列线性规划模型

式中，T表示运输时间上限；c_ij表示从产地A_i到销地B_j的单位运费；t_ij是（2-23）式定义的实际运输时间。