本节中我们将利用参考文献[39，49]中的两个实例，通过Lingo软件编写程序，直接求解数学规划模型，寻找最短时限运输问题或扩展情况的最优解，并把计算结果与文献中的手工计算方法得到的结果加以比较。

例1^[39] 某地发生大范围洪灾之后，发现有5个居民点出现某种流行病，急需从3所医院抽调医护人员赶往疾病发生地救治病人，各个居民点需要医护人员的数量、各医院抽调医护人员的数量及从各医院到各居民点所需要的时间如表8-1所示。问如何组织调运才能使医护人员在最短的时间内全部到达居民点？

表8-1 医护人员供应量和需求量及运输时间t_ij （单位：h）

这个例题没有考虑到运输量对时间的影响，符合本文中讨论的模型（8-1～8-7）。利用Lingo软件编写程序，直接求解模型得到以下结果，见表8-2。

表8-2 最优调运方案

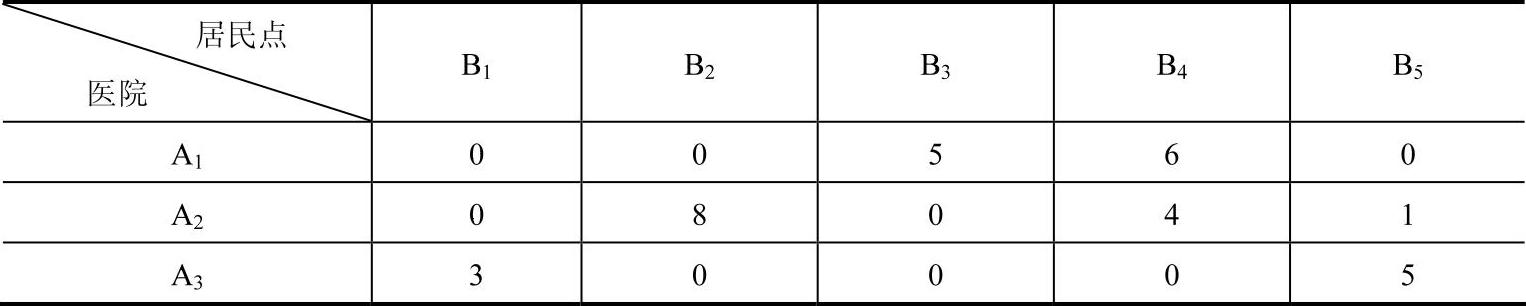
完成整个调运任务需要的最短时间6h，最优的派遣方案为从A₁医院派出5个医护人员到B₃居民点，6个到B₄居民点；从A₂派出8个到B₂居民点，4个到B₄居民点，1个到居民点B₅；从A₃派出3个到B₁居民点，5个到B₅居民点。该结果与参考文献[39]中的计算结果完全相同。

例2^[49] 某地区发生地震，发现有2个村庄受灾，需从3个城市调运救援物资。已知调运救援物资量和基本运输时间如表8-3所示。假设实际运输时间是运输量的二次函数，影响系数α_ij如表8-4所示。

表8-3 t_ij和调运物资量 （单位：t）

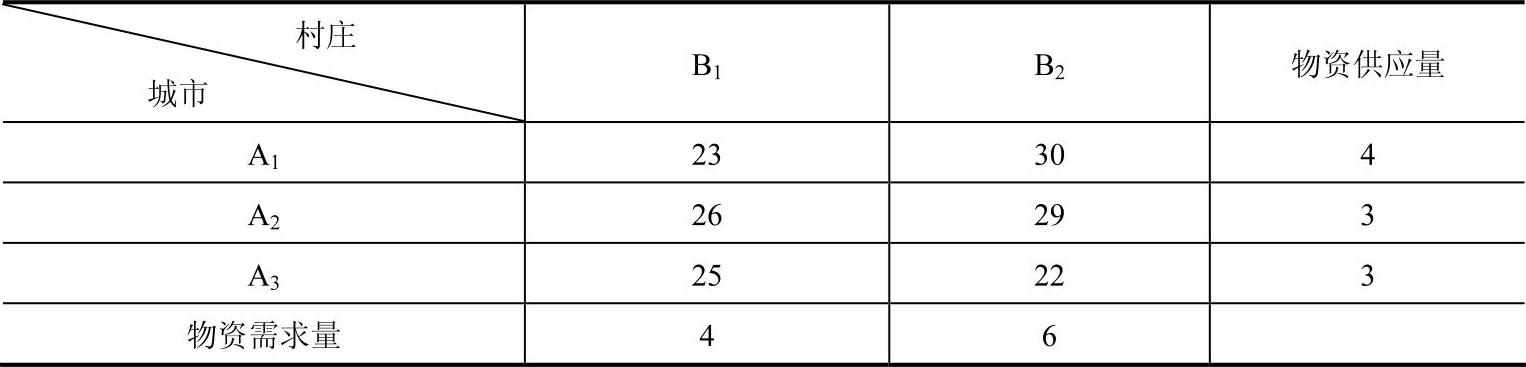
表8-4 影响系数α_ij

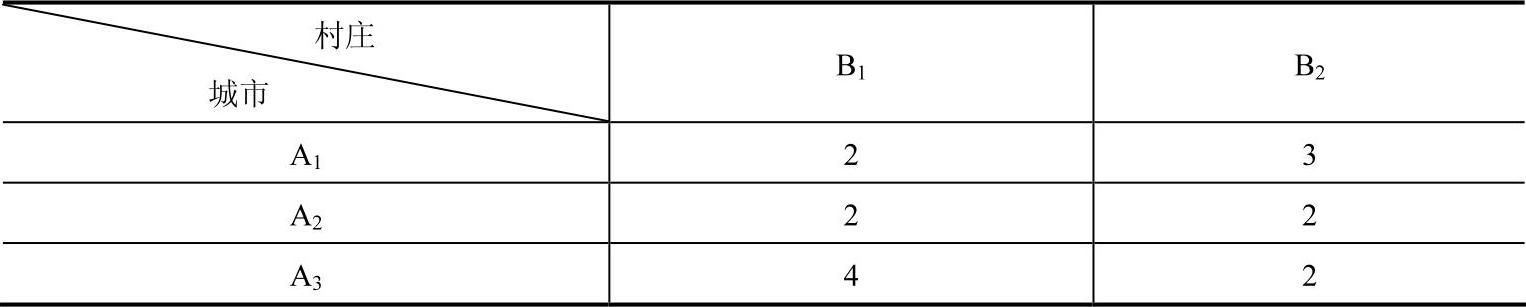
参考文献[49]中作者利用基于网络流算法的二分搜索求解法，求得的每条路线上的货物运量及实际运输时间分别如表8-5和表8-6所示。(www.daowen.com)

表8-5 参考文献[49]中得到的最优货物调运方案 （单位：t）

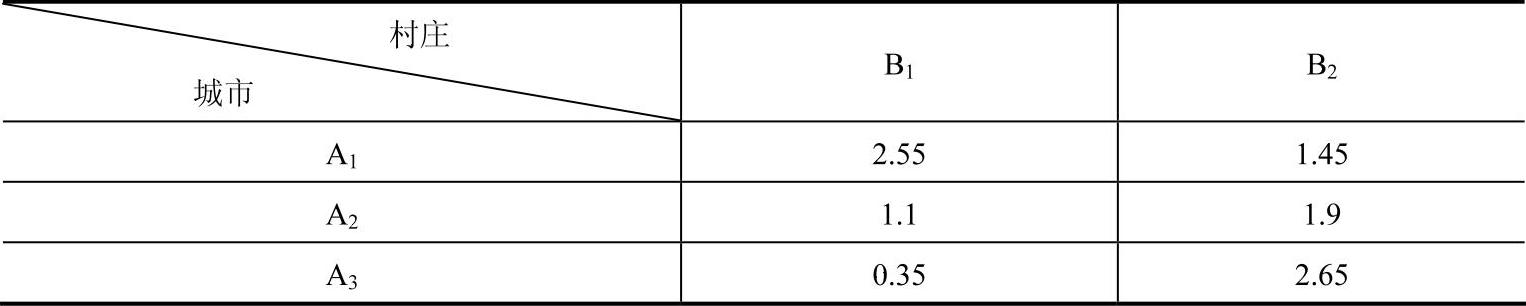
表8-6 参考文献[49]得到的调运方案对应于各条路线上的实际运输时间 （单位：h）

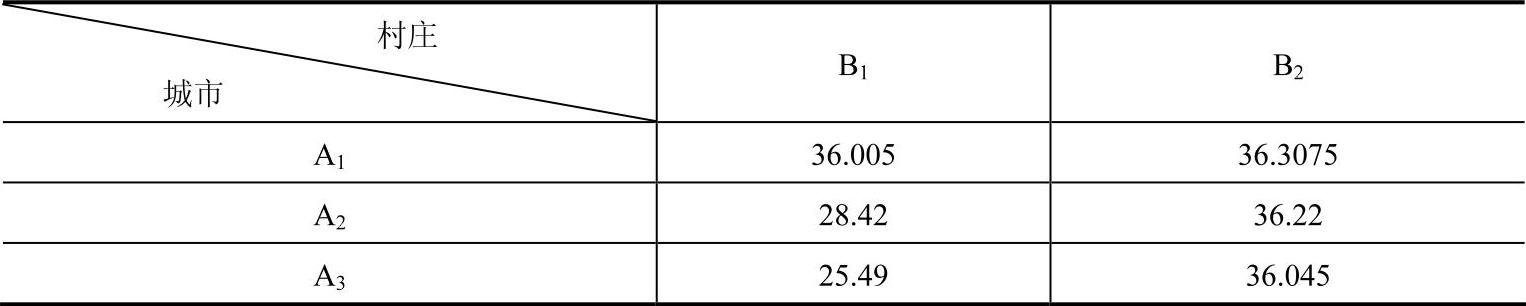
从表8-6中我们可以看出，按照表8-5的方案完成整个运输任务需要的时间为36.3075h，即从A₁到B₂的运输时间。由于其他格点对应的运输时间均小于36.3075h，因此，可以通过闭回路方法调整运量，使得A₁到B₂的运量降低，从而减少该路线上的运输时间，进一步减少目标函数值。因此，参考文献[49]求出来的结果并不是全局最优解。

利用模型（8-8～8-14），编写Lingo程序对本问题进行求解，得到的结果如表8-7和表8-8所示。

表8-7 利用Lingo软件求出的最优货物调运方案 （单位：t）

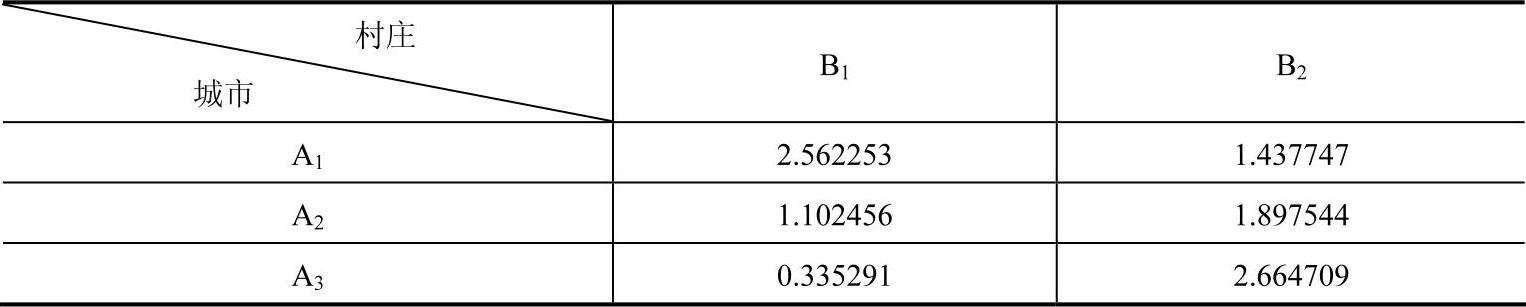
表8-8 最优调运方案对应于各条路线上的实际运输时间 （单位：h）

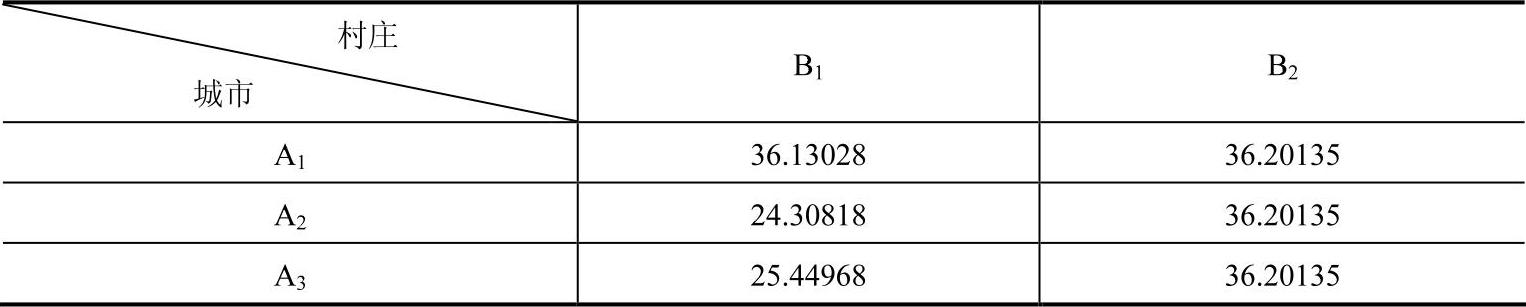
从表8-8可以看出，完成整个调运任务所需的最短时间是36.20135h，从三个城市到B₂村庄的所有路线上的时间都已经达到了最大值36.20135h，因此，我们看到B₂所在列的运输时间都是一样的，而且是所有道路上运输时间的最大值。此时若再对表8-7中B₂列的运量进行调整，必然会使该列某条路线对应的运量增加，从而增加其运输时间，进而导致整个问题的目标函数值增大。因此，当运输表中某一行或某一列的所有格点对应的实际运输时间同时达到最大值的时候，整个问题的解必然为最优解。故表8-7对应的运输方案就是例2的最优运输方案，按照这个方案安排运输，需要的时间是36.20135h。

将表8-6和表8-8进行比较，我们发现，表8-8中求出来的结果是整个问题的全局最优解，而表8-6求出来的不是全局最优解。虽然两组解对应的目标函数值相差不大，但由于我们研究的是救灾物资的调运问题，在灾害发生时，时间就是生命，一小点的时间延迟都可能会带来巨大的损失，所以，如何能尽快找到解决问题的最优方案是解决这类问题的关键因素。借助于计算机软件求解，不仅可以缩短计算时间，而且可以找到问题的全局最优解。