最短时限运输问题可描述为：已知m个产地A_i，i=1，2，…，m，可生产某种物资，其产量分别为a_i，i=1，2，…，m，有n个销地B_j，j=1，2，…，n，销量分别为b_j，j=1，2，…，n。从A_i到B_j的最短时间为t_ij。假定各个产地都有足够的运输工具运送货物去各个销地，问如何组织调运，才能在最短时间内完成物资调运工作？

参考文献[39]将该问题归结为求一组x_ij，i=1，2，…，m；j=1，2，…，n，满足

使最终的到达时间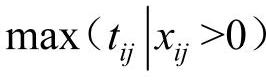为最小。其中x_ij表示从产地A_i运往销地B_j的货物数量。

由于该模型的目标函数不是决策变量的线性函数，因而不是一个线性规划模型。注意到目标函数是一个有条件的极大极小化函数，通过引入一组0，1变量即可把该问题表示成一个线性规划模型。

引入0，1变量(www.daowen.com)

及变量y，则最短时限运输问题可以转化为以下线性规划模型

其中，目标函数（8-1）式表示所有运输路线上所用的时间上限最小，即完成所有运输任务的时间最短；约束条件（8-2）和（8-3）表示各个供应点的货物全部运出去，各个需求点的需求量恰好得到满足；约束条件（8-4）是完成整个运输任务的时间上限与各条路线上的运输时间的关系；约束条件（8-5）是对变量z_ij和x_ij的取值关系的说明；约束条件（8-6）和（8-7）是变量取值的说明。

显然，模型（8-1～8-7）是一个线性规划模型，可以使用求解线性规划的软件进行求解。