在一个给定的物流配送网络图中，共有11个需求点，分别用序号1、2、…、11表示。该区域内有一条河，河上有两座桥，分别用P、Q表示，各点之间的距离关系如图7-5所示。已知B公司已经在需求点1、2和3点处设置了物流配送中心，现A公司欲进入该市场，假设A公司在每个需求点处都可以建立物流配送中心，如果A公司可以使用的最大投资预算是5OO万元，在各需求点建立物流配送中心的建设成本均已知。图7-5中各个需求点旁边的方框内的数字分别代表在该点建立物流配送中心的成本以及该需求点的需求量，假设产生聚集效应时的参数分别为α=0.2、β=0.15，问A公司应该在哪些需求点处建立物流配送中心才能使总利润达到最大？

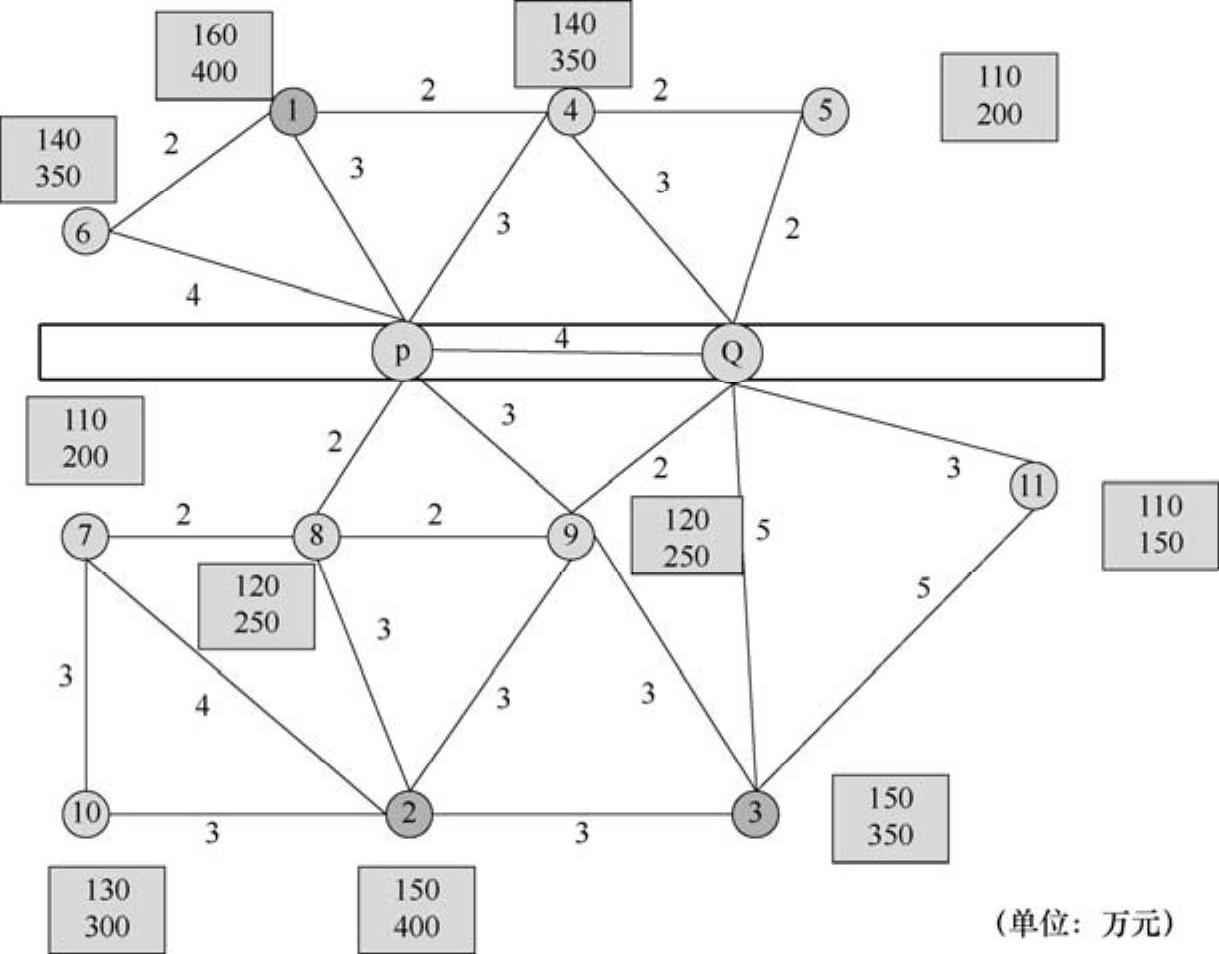
图7-5 各个需求点的位置关系及需求量、建设成本示意图

本例中各个需求点处均可建立配送中心，因此，设施备选点与需求点位置相同，B公司的已有设施分别在需求点1、2、3处。为了简化求解过程，我们先利用Matlab求最短路算法的程序求出各个需求点到设施备选点之间的最短距离，结果见表7-2。

表7-2 个需求点到设施备选点的最短距离表 （单位：km）

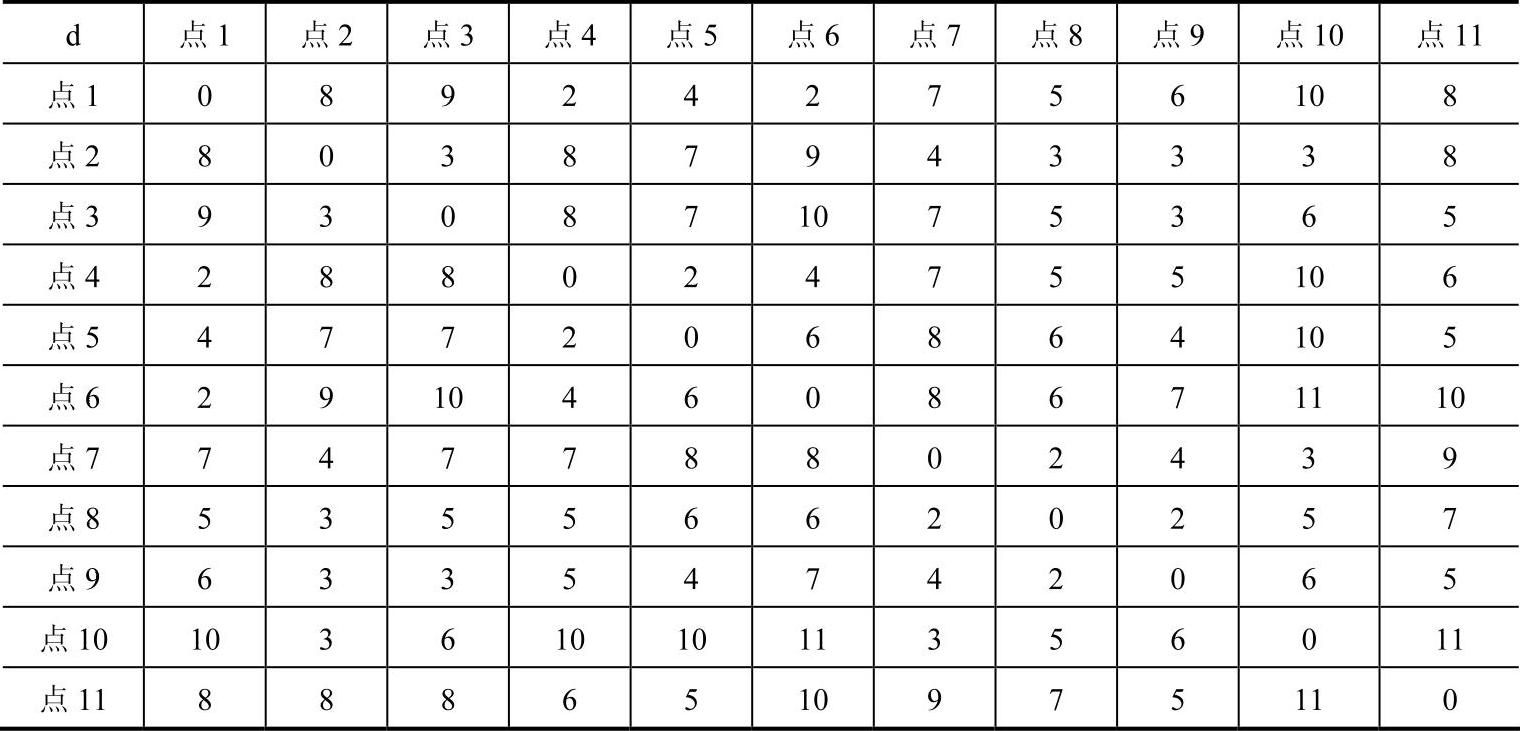
利用表7-2的信息，根据公式（7-8）～（7-11）可以求出各个需求点i对应的d_iB及相应的b_i=（b_i1，b_i2，…，b_ik）。

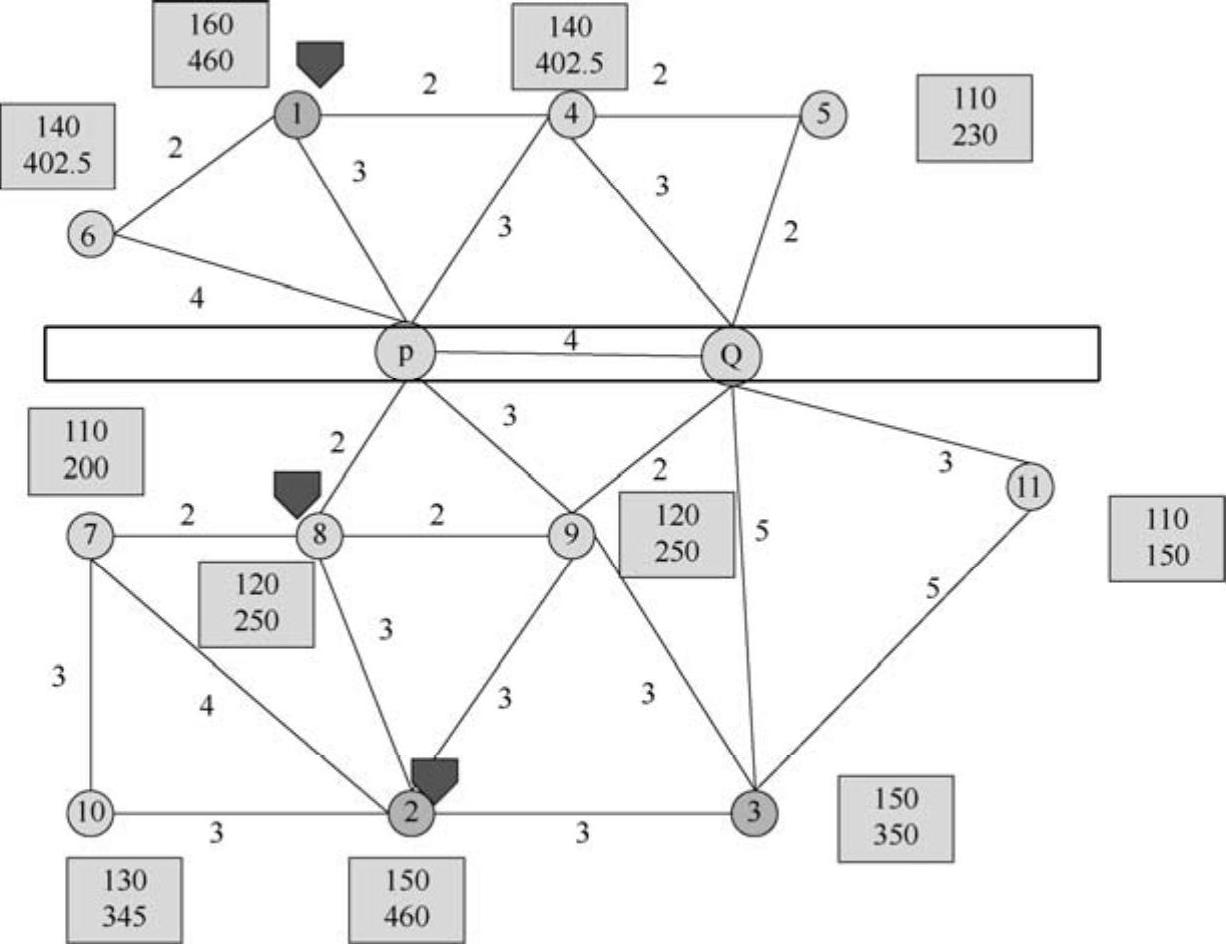
然后，将相关数据代入利用Lingo软件编写的求解整数非线性规划模型的程序中，可以求出使A公司利润达到最大的选址方案。即A公司应该分别在点1、2、8处建立物流配送中心，所得的最大利润为142O万元，见图7-6。按照该方案建立配送中心，需求点7、8、9的需求量完全由A公司满足，需求点3、11的需求量完全由B公司满足；由于点1和点2处原本已经有B公司的设施，因此在点1和点2处将产生聚集效应，点1、4、5、6的需求量将增加15%，增加后的需求量由点1处A、B公司的设施平均分摊满足；点2、1O处的需求量增加15%后由点2处的A、B公司设施平均分摊满足。受聚集效应影响，点1、2、4、5、6、1O处的需求量分别增加了15%。

(www.daowen.com)

图7-6 A公司选址结果图

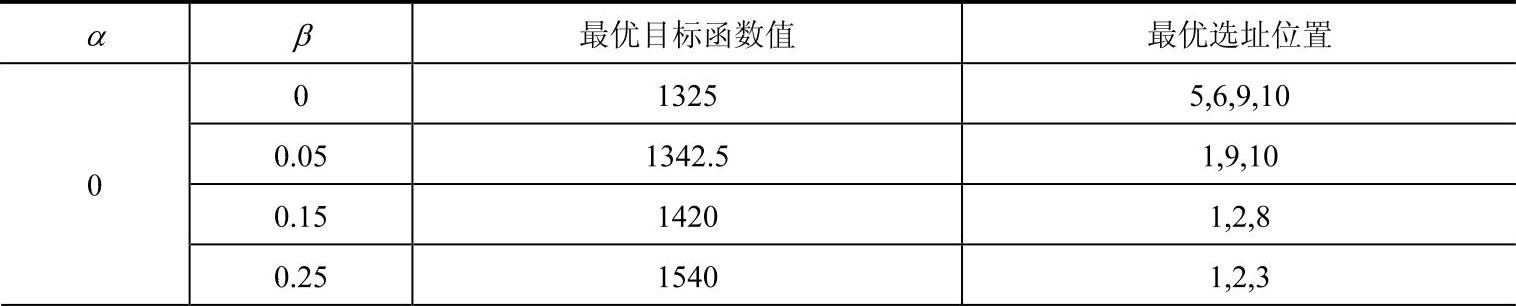
为了研究聚集效应对应的两个参数（距离折扣率、需求增长率）与选址结果的关系，本节分别选取了多组不同的距离折扣率和需求增长率参数并计算了各组参数下的最优选址结果，见表7-3。

表7-3 不同参数下的选址结果表

（续）

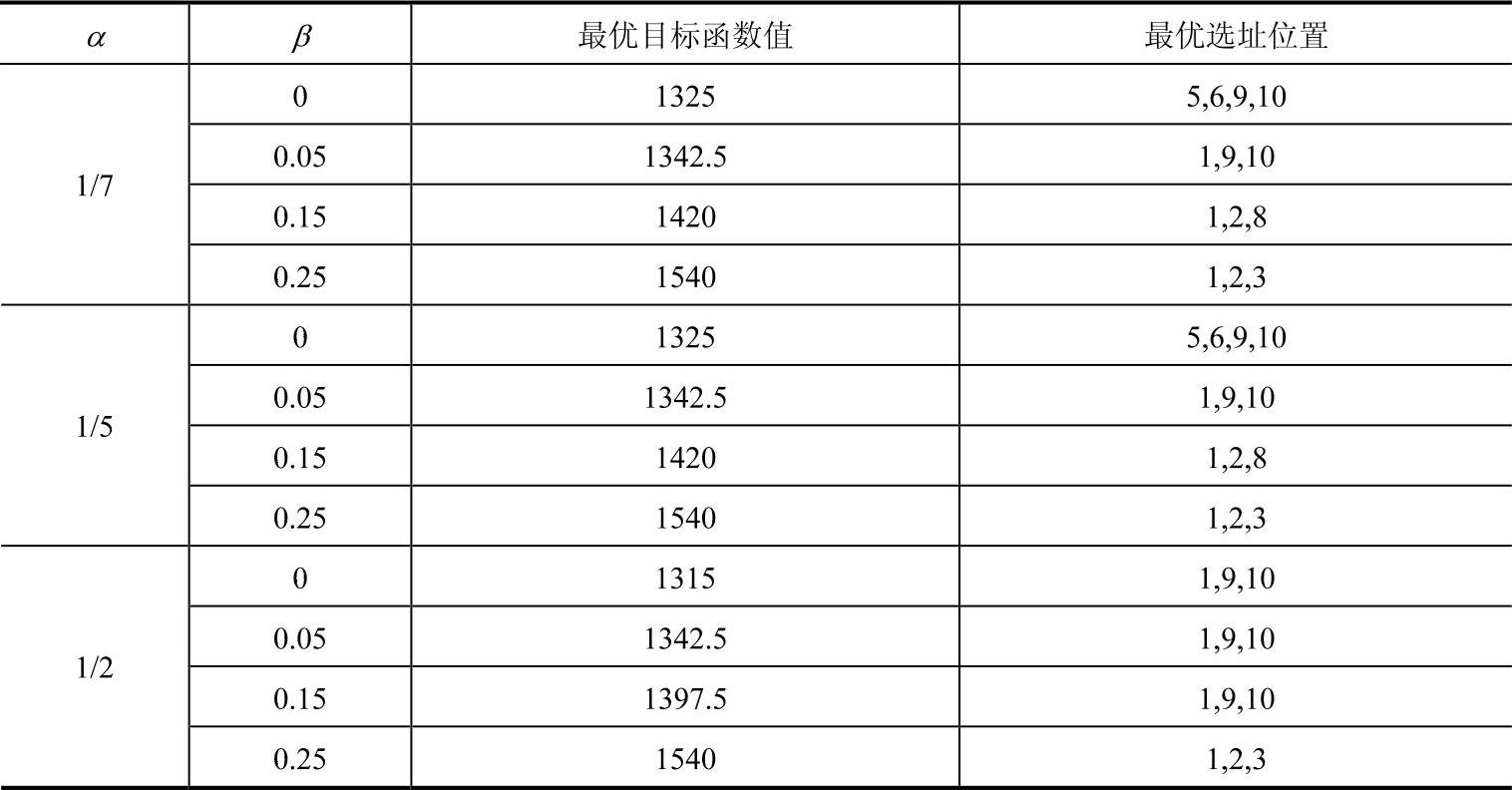
从表7-3中可以看出，当需求增长率相同时，不同的距离折扣率下的最优目标函数值和最优选址位置基本相同；当距离折扣率取1/2时，部分最优目标函数值有所下降，最优选址位置部分发生变化，可见距离折扣率对选址结果的影响并不大。当距离折扣率相同时，随着需求增长率的增加，最优目标函数值逐渐增加，A公司的最优选址位置也会相应发生变化，逐渐向B公司的已有设施位置靠拢，这是因为，随着需求增长率的增加，整个市场的总需求量逐渐增大，此时，A、B公司都将从聚集效应中获得一定的市场份额，从而在一定程度上实现双赢。这就是我们经常看到麦当劳和肯德基总是出现在同一个地方，而每家都是人员爆满的原因。聚集效应的产生对需求起着很大的促进作用，从而更能增大其利润。